В минувшую субботу прошел второй квалификационный раунд олимпиады по программированию Russian Code Cup 2012.
В данной статье я подробно разобрал задачи, вынесенные на конкурс, а также поделился статистикой раунда. Я постарался разъяснить детали настолько, чтобы решение задач было понятно даже тем, кто еще делает первые шаги. Также данный материал поможет получить представление, какой сложности задачи предлагаются на отборочных этапах чемпионата по программированию Russian Code Cup.
http://habrahabr.ru/company/mailru/blog/145262/
В это воскресенье, 10 июня, в 11:00, будет проходить последний квалификационный раунд, из которого две сотни участников перейдут в «полуфинал» — отборочный раунд. На втором раунде для этого достаточно было решить две задачи — одну простую и одну сложную, и уложиться при этом в половину отведенного времени. Ждем вас в воскресенье и желаю удачи!
Объясните пожалуйста мне: почему в Е не O(M(logN)2).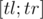
и нужно найти самый левый индекс i такой, что 
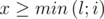. Тогда нужно же за log(N) узнать минимум на 
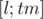и решить куда идти. Получается log(N) уровней и на каждом по log(N) действий?
Добавили открывающуюся скобку в позицию l. Допустим мы стоим в вершине отвечающей за
UPD: кто минусует, мог бы и написать, где у меня бред.
Если на каждом шагу заново считать минимум на отрезке, действительно получится log^2.
Если я не ошибаюсь, запрос за log(N) получится, если не каждый раз вычислять минимум на [l, tm], а действовать так:
1) Запрос ([tl, tr], [i, N], x) будет возвращать первый индекс на пересечении отрезков [tl, tr] и [i, N], где глубина равна x, или что-нибудь нехорошее, например "-1", если такая глубина недостижима.
2) Если [tl, tr] полностью входит в искомый интервал [i, N], то минимум глубины на [tl, tr] уже вычислен и хранится в рассматриваемой вершине. Тогда мы можем или сразу вернуть -1, или, зная что ответ на этом отрезке, спускаться в левую или правую половину, так как все подотрезки тоже входят в [i, N] полностью и их минимумы вычислены.
3) Если [tl, tr] не пересекается с [i, N], возвращаем -1.
4) Если наблюдается частичное пересечение, сначала рекурсивно найдём ответ на пересечении [tl, (tl+tr)/2] и [i, N], а если он -1, то поищем и на правой половине.
Спасибо, теперь всё понятно.
В D прошел перебор. Скажите пожалуйста кто-нибудь : так должно быть? просто мне не совсем понятно, как оценить ассимптотику такого решения(пребора).
Вы бы поподробнее написали, в чём заключался перебор.
Простой перебор- выбираем для каждой сложности одну задачу и проверяем что бы по условию не пересекались темы и все темы были задействованы. Который кстати ломается на простом макстесте где нет ответа при n=300 и d=50 и по 6 задач каждой сложности . И все задачи с k=0.