→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 22:18:19 (k3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










I just tried to register but I'm getting "You're not allowed to log in from this location." Is it not an open contest?
Change the contest from HNOI to COCI.
Reminder: less than 2 hours left.
Now it's 1 hour.
I wonder what happened to the author of the second task. Why the footnote is so sarcastically?
Firstly, I scared input of 50 :D
Poor input of 50.
The problem statement of second task is so long it's disgraceful.
How to solve B (80) problem ?
Look at divisors of 2N.
Hint: sum of l,l+1,...,r-1,r is equal to (l+r)/2.0*(r-l+1)
try iterating over every possible value of (r-l+1)
You can solve in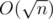
You will understand from that :
sum of 2 adj. numbers: m + (m + 1) = 2m + 1
sum of 3 adj. numbers: m + (m + 1) + (m + 2) = 3m + 3
sum of 4 adj. numbers: m + (m + 1) + (m + 2) + (m + 3) = 4m + 6 .. etc..
How to solve C? I used bitmasks for 40pts.
This might be overkill.
Let's denote the amount of a-s, b-s and c-s Slavko has for some some suffix of Mirko's string as sa, sb, sc. Also denote the amount of a-s, b-s and c-s in the suffix as ma, mb, mc. Then that suffix is solvable with the given letters iff the maximum flow of the following graph is sa + sb + sc:
Now we can iterate over Mirko's string and choose the lexicographically smallest character so that the remaining string is still solvable with the remaining letters.
huh, at least I'm not the only one who did that :D
Task Igra: implement an O(n) function to answer "is it possible to arrange a valid string if we have (a1, b1, c1) free characters against (a2, b2, c2) already placed characters (notice that a1 + b1 + c1 = a2 + b2 + c2). To do it you can iterate over what part of a1 goes to b2, and then all the rest if fixed and can be checked with some ifs.
Now you can iterate over each character of answer string and try to place a, then b, then c and check if it is correct. It is O(n2), obviously. By the way, the function is some kind of maxflow, so it can even be solved in nearly constant time, making O(n) operations total.
I tried to fill a2 with b1 and c1 by first giving all the b1 and then c1...another possibility is by giving all c1 and then b1. I generated 8 such possible ways.
Is it wrong? :/
You can just pick the letter greedily, checking if choosing such letter and you can still have a valid string afterwards.
e.g. if you choose 'a' at pos i, you need to make sure no. of 'b' in Slavko[i + 1 .. n] <= (a — 1) + c, no. of 'c' in Slavko[i + 1..n] <= (a — 1) + b. you can do this O(1). where a, b, c are the number of letter that Mirko still have.
So overall time complexity is O(N).
Did you get full score for that approach? Because I did the same and got only 30 points (it is possible that my code has a bug).
Yes I got full score with it. qjnUOH
Thank you
I got 30 too, my error was that I was allowing negative frequencies.
Exactly the same bug.
How to solve 140pts?
I wonder why the limits for third task are so small. Isn't there an O(n * alpha^2) solution?
UPD: seems like my solution is wrong
I submitted an O(n^2) solution, but I think that it could be changed slightly to an O(n) one. How did you get an alpha^2 factor?
First alpha for iterating over every character, second alpha for checking if this character can be inserted (if it doesn't make some of the remaining characters unusable)
Oh, I thought that by alpha you meant the inverse Ackermann function
how to solve F?
I can solve it only for 64 points with a weird Gauss Elimination but I have no idea how to do it for max.
I didn't solve it (made pretty bad mistake), but I think this is the intended solution.
The only thing left would be to find σ, which can be done using Knuth-Morris-Pratt.
So this solution runs in O(M) time.
Got it. Thanks.
Is it just me or COCI's are becoming harder and harder?
You can look at the scores of people in past contest to compare. Write back if you find something interesting.
Oh! I see it. One contest is easy the next is difficult :P
I think this contest was harder than usual.
In 5th round I got 434 points, 6th round was 350 points and now I didn't even solve three problems in this round :(
Or maybe the previous rounds this season were easier than usual? At least this is how I feel about it.
What's an expected value?
Sum of every possible result divided by the number of these results. If a result can be obtained in two different ways it should be counted twice.
I haven't read the problem asking for expected value. I'm giving the general meaning
Thanks
That is correct only if all results have equal probability.
The general definition of expected value is :
Let's say that there are n results of something with values
a[1],a[2],..a[n-1],a[n] and the probability of the ith result to appear is p[i], then:
The expected value=sigma p[i]*a[i]
Fourth problem (120) may fail because of recursion?
How long does it normally take for COCI results to be final? It's my first time competing in a round.
Like an hour. But initially the results only appear at the evaluator page, it takes a while before they appear at hsin.hr/coci
you can see them now
Azret was the first place in 6th round but he scored 130 in this contest. Isn't it weird?
I got a solution for problem D that got TLE on 2 last testcases. How can I improve it?
First, treat the scale as a binary tree (left child = left beam, right child = right beam, weight = leaf node). There will be maximumly 3n nodes in this tree.
Call dpu the smallest sum (in binary form) for a balanced subtree in vertex u. Then:
We got a O(n2) solution now. How can we make this faster?
Since dpu is now a string, multiply by 2 also mean add character '0' to the end of the string. So, with careful implementation using pointer, "assigning" value for all dp states will take totally O(n). What about time needed to compare the strings from two children? It's in the worst case (The tree look like an segment tree with value of all leafs equal each other). So we got a
in the worst case (The tree look like an segment tree with value of all leafs equal each other). So we got a  solution.
solution.
My code
My solution was saving the values and the exponential of two considered that the answer is one of the node * power of 2. This give a linear solution. The last two were hard so I luckily got 12th by solving first 4 problems lol.
Sorry if this is stupid, but how to prove correctness of the DP for an internal(scale) node? I mean if we have scale with children having weights a and b(a ≤ b) we'd have to add b - a weight to the left child, but how do you know that it can be done while maintaining the current balance within that subtree? Wouldn't it be required for b - a to be divisible by 2height where height = height of the node from the bottom?
My solution for D got just 54pts. I think my approach is correct —
For all the weights, I found the wt such for maximum value — w[i]/pow(2,level[i]). Answer is concatenation of binary representation of wt and level of wt times '0'.
also I took care of the fact that level can go upto 10^6.
My Code
Where am I wrong?
Probably handling 106 strings of length 106 is too much. It is better to represent the numbers in the form of a·2b where a is some odd integer.
I didn't made strings of length 10^6. Check my code. I got just 54 pts.
Could you post a link to your solution? Thank you in advance. :)
Am I the only one, who thought, that in the 4th problem you are only allowed to add weights to the existing weights (in other words, to the leaves of the tree)? Got only 54 points during the contest because of that and full score in the analysis mode when I decided to leave this assumption alone (and I believe, that my first assumption is way more intuitive).
I assumed that and got 120. You were wrong elsewhere.
What does your solution produce for the following test case?
2
2 -5
-2 -2
According to my AC solution, the answer is 1010, and according to my failed slution, the answer is 1100
And one more thing: if we assume, that we can only add the weights to the leaves of the tree, the total weight should be divisible by 2treeDepth, which, I believe, is not true for the fifth test in the testset
This is not true. See the first clarification on the message board — you may add any real number to the leaves. In your example, we can add 0.5 to both of the "2" leaves.
Oh, I've missed that clarification. Now it all makes sense: the problem, where you are allowed to put the weights to non-leaf vertices and the problem where you are allowed to add any real number to the leaves are equivalent. Thanks!
How to solve the 5th problem?
Sketch of the solution (I am an author of the problem):
Take any 3 noncolinear points and bring them all to the [5, +inf] x [5, +inf] quadrant of the plane. It can be seen that such series of moves exists if you observe the tiling of the plane by parallelogram generated from those 3 points. Now, you can just use BFS to find shortest series of moves to bring those 3 points to that part of the plane. Since coordinates are small you can check all possibilities and see that in worst case this takes around 1200 moves.
Last, you can see that after you have points A, B in quadrant [5, +inf] x [5, +inf] you can move any other point C to first quadrant with just one move.
Form problem D, it seems like I had to use linear diophantine and solve it using extended euclidean algo but I have no idea was it is an just gave up :(