zephyr_23's blog

Pollard rho factorization doubt.
By zephyr_23, history, 7 years ago, In English

I am reading the article on this website https://www.cs.colorado.edu/~srirams/courses/csci2824-spr14/pollardsRho.html to understand Pollard rho factorization.

I will explain my doubt with an example.

Suppose for N = p * q, we have 35 = 5 * 7 where N = 35,p = 5,q = 7.

Probability of finding factor 5 from [1...35] is 1 / 35.

To increase the probability of getting the factor 5, we search for number x such that GCD(x, N) = 5. Numbers 5, 10, 15, 20, 25, 30 satisfy the equation GCD(x, N) = 5. So probability of finding factor 5 increases to 6 / 35.

Now they have mentioned that to increase the probability further, we find pairs of numbers such that |Xi - Xj| = Yi where Yi is 5, 10, 15, 20, 25, 30.

Number of pairs satisfying the criteria |Xi - Xj| = 5 is 30 * 2 = 60, similarly number of pairs satisfying |Xi - Xj| = 10 is 25 * 2 = 50 and so on..

So to get factor 5, we need to search (30 + 25 + 20 + 15 + 10 + 5) * 2 pairs out of 35 * 35 pairs. So the probability of getting required pair is (210) / (35 * 35) = 6 / 35 which is same as the one where we found factor 5 using GCD(x, N) without searching for pairs.

So my doubt is, to find required factor, why do we search for 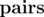such that GCD(|Xi - Xj|, N) = p instead of GCD(Xi, N) = p as their probabilities are same ?

  • Vote: I like it
  • +37
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

The probability is the same but you need to take less Xi. For example you take k elements Xi, or you can take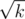 elements Xi and take all pairs — the amount will be the same (roughly). However, you can note that you still have to check each element/pair and the time complexity is still the same. And here comes the Pollard rho algorithm which performs a random walk and captures the correct pair at some point.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes, I understand that pollard rho performs random walk and captures correct pair. But why can't pollard rho perform a random walk to capture a single value as I asked in the question? According to the probability calculation, it should not matter whether we search for a pair or a single value right (as probabilities are same) ?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You can do walk and capture single value but then you have to walk mod N through roughly N1 / 2 values until you get multiple of p (which you get with probability 1 / q).

      To see why rho is better, consider your walk mod N but modulo p. We expect to have a loop in values mod p after p1 / 2 ≤ N1 / 4 steps. Then a cycle-finding algorithm allows to find two values ai, aj that have same value mod p but probably have different values mod q. The time complexity is proportional to size of the loop. That's where you get improvement and get N1 / 4 instead of N1 / 2.

      → Reply