Добро пожаловать на 2013-2014 CT S01E01: Extended 2000 ACM-ICPC East Central North America Regional Contest (ECNA 2000). Продолжительность тренировки — 5 часов. Тренировка открыта как для команд, так и для индивидуальных участников. После ее окончания вы можете дорешивать задачи тренировки или поучаствовать в ней виртуально, если не смогли принять участие одновременно со всеми. Пожалуйста, участвуйте в тренировке честно.
Так как это тренировка, то возможно набор задач будет расширен, если для значительного количества участников он окажется простым.
Удачи!
Произошла странность. Я был зарегистрирован. Потом поклацав по рейтингу увидел что мне опять доступна регистрация, т.е. произошла разрегистрация меня, хорошо что заметил.
please do not use register mode for it. I could not find any information about registration.
EDIT: I found the registration option there. Please NEGLECT the comment.
Существует ли какой-нибудь фильтр, чтобы видеть только саратовские команды в ранклисте?
Специального нет, добавь всех в друзья и нажимай просмотр друзей.
Я правильно понимаю: для того, чтобы команда оказалась в друзьях, в друзьях должен быть тот человек, под личным аккаунтом которого они сейчас пишут? Имхо, не очень удобно выискивать команды в ранклисте и добавлять их по отдельным участникам.
Или в друзьях должен быть любой человек из реально пишущего состава команды (который может не совпадать с полным составом)?
Вроде любой из команды.
Я добавила Сухова, но его команда не добавилась. Видимо, потому что именно на этом контесте его нет.
In problem B: "The judges input will be such that the maximum value for any poly-polygonal number will fi t in a long variable."
How i suppose to know what long are authors using? 64-bit? 32-bit?
By looking at the time: it's regional in year 2000
But in Java long was always 64 bit. Or i'm wrong?
Sorry, I was thinking about C++ :)
We had the same problem. All the contest I couldn't get how to solve the problem. But at the end of the contest we saw clarification and it helped.
I saw clarification too late, but the problem is that some team get answer for this clar in the middle of the second hour and they were not public, so this is very sad...
Как решалась задача А?
Правильно ли я понял, что в задаче А необходимо найти миностов с условием того, что парк имеет степень меньше либо равную заданного числа?
Правильно.
Правильно ли такое решение (ВА 2)? Переберем за 2^n врешины, которые едут сразу к парку, а на оставшийся граф достроим до остова алгоритмом Крускала.
Доказательство : рассмотрим те вершины, которые мы перебрали. Сожмем им в одну вершину, получим дерево. Найдем остовное дерево. Получим такое же остовное, как если бы мы не сжимали.
Правильно, если вы перебираете вершины, только смежные парку. Ну и, естественно, нужно проверить что Крускал нашел остовное дерево, а не остовный лес.
У нас был точно такое решение, но почему то получили ошибка исполнения на тесте 7. Вот код.
Капитан подсказывает, что у вас бага. А также капитан подсказывает,что в графе может быть больше 30 ребер, так что рекомендую ваши массивы сделать побольше. А еще от меня рекомендация — инициализировать значения/обнулять переменные (типа n у вас), несмотря на то, что компилятор это сделает сам, в случае если переменная глобальная. Просто потом баги быстрее ищутся, да и код приятнее читать.
Спасибо.
Sir , Is it possible to view the solution of other contestants after the contest gets over in these training seasons ????
I guess that there may be something wrong with the spj of Problem K. See these solutions: http://mirror.codeforces.com/gym/100227/submission/4444208 http://mirror.codeforces.com/gym/100227/submission/4442973
Their Case 3 both are wrong from my understanding. Did I misunderstand something?
The checker was incorrect. It is fixed now.
How to solve problem K?
I guess it has something to do with the Erdős–Gallai_theorem.
But during the contest I got AC by a naive random algorithm:
Can you explain what do you mean exactly? What is the list? For what do we need to use it.
The task asks us to extend a list of number (with numbers already in it) such that the result will be a degree sequence of a simple graph. (The matrix is the adjacent of that graph)
It's easy to check if a list of number is a degree sequence or not. (e.g. by Erdős–Gallai_theorem)
And my solution is: while the list is not a degree sequence, extend it by an element in it randomly. You can see my code 4444583.
You can get the solution by induction, or in other words by recurrence.
Sort input array, pick largest and smallest element. Then build matrix of size largest x largest, where the first smallest rows and the first smallest columns contains only ones (except main diagonal).
Then erase these two elements from array, subtract from all other elements of array a value smallest. Solve the problem for smaller array. And arrange result of smaller solution in our matrix in a right way (you can guess how yourself).
That was one of the approaches I tried... but I got confused on the irregularity that the diagonal zeroes cause and in the end decided to solve other problems...
Doesn't seem very intuitive to me. May be you could help. So when we pick the largest and the smallest element then we set the first row(and correspondingly the first column) to 1s.
Eg:
if input is
2
4 2
then I would build a matrix with something like this :
0 1 1 1 1
1 0 X X X
1 X 0 X X
1 X X 0 X
1 X X X 0
So firstly how do I fit in the smaller number in this matrix.
Next how would I arrange my smaller solution to the larger one. For example it might be the case that the matrix size is larger than largest x + 1. In that case how do I work.
So you could probably help by working out an example say:
2
2 3
Solution:
5
0 1 1 1 0
1 0 1 0 0
1 1 0 0 1
1 0 0 0 1
0 0 1 1 0
Скажите, а задача про лесницы(Н) решаеться бин. поиском по ширине улицы? Точнее мы для выбора вертки бин. поиска строим лесницы, находим их пересечение и проверяем высоту пересечения с данной в задаче. Доп. критерий останова точность 1e-4.
Про лестницы задача L. Бин. поиском по ширине улицы решается. Я точность 1e-6 брал.
а можете поподбробней объяснить? А то я что-то не совсем понял.
Ответ не может быть больше чем самая короткая лестница. Следовательно в начале нижняя граница бин. поиска 0. А верхняя min(x,y). Теперь такая проблема: Как по ширине улицы найти высоту пересечения. Пусть лестнице с длиной Y принадлежат точки: (0; 0) и (x1; y1). Где x1-ширина улицы, а y1 по теореме Пифагора находится. Лестнице с длиной X принадлежат точки: (0; y2) и (x1; 0). y2 находится по тому же принциу что и y1. Зная точки можем построить уравнения прямых, решая систему из 2х уравнений находим координаты точки пересечения. Нас интересует только координата Y, если она больше C, то увеличивается нижняя граница бин. поиска, иначе уменьшается верхняя.
Очень хорошо. Почти всё понял. Осталось одно: когда мы находим ординату точки пересечения, она же получается y = (y1 * y2) / (y2 + y1). Нам же неизвестны ни y1, y2. Как посчитать y?
Возьмём линию длины Y. Исходя из моего сообщения у неё есть две вершины с координатами: (0; 0) и (x1; y1). x1 это ширина улицы, Y-длина лестницы. Получается прямоугольный треугольник, у которого нам известны катет и гипотенуза. Длина второго катета будет равна y1. Аналогично для y2.
Any intuition on Problem I. I really suck at Geometry !
Why cant I view any solution after the contest is over. Are they not public ?
In Gym, you can't view others' solutions until you solve that problem first.
But without any editorial or without even viewing others solutions, how can i learn something new ?
You can view my solutions (I solved all problems but 2) here
Wow that's great.. Hope this will help me a lot.. Thanks a ton..
Thank you
Possibly i don't understand problem of accuracy in double. In problem L i've wrote binary search with such conditions link1/ It's got WA2. Then i got AC changed this snippet like this link2. Full AC code. Explain me please what's the difference between this snippets of code. I don't want to repeat this mistake.
How to solve problem A ? I am stuck at it.
you're to find Minimum Spanning Tree with an additional rule — capacity of parking of Park .
to solve the problem , for any subset of nodes , pick the edges from this nodes to Park ( member of this set directly goes to Park ) and run a MST algorithm on rest of graph .
sorry for poor english :D
There is faster solution: iterate over masks which contain exactly k ones, but not include in st and then find mst. Complexity is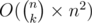
.
what's happen when number of edges to Park is less than K ??
It is obvious, you can just find mst or in the very beginning just make K = min(K, park_degree) and solve as I said above(There will be only one iteration).
This has worst case when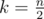
. The central binomial coefficient is asymptotic 
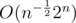, so it's still 
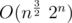asymptotically in worst-case.
I have a solution which works in O(n 2n) time. For every subset and vertex not in it, we calculate the minimum distance of this vertex from the subset (minimum of distances of it from vertices of the subset), by taking the pre-calculated minimum from the subset without one vertex (the result is the minimum of this and the distance of our vertex from the one excluded from the subset). Now, finding MST of a given subset takes only O(N) time: we try all possible choices of the last vertex added to make this subset, and for every one of them, we already know the cost of adding it to the subset excluding this vertex. Of course, the starting subsets are the ones with at most k+1 vertices: the park and several vertices connected directly to it.
I couldn't understand the solution you are proposing. I am doing something similar:
with n park edges and k parking lots:
iterate all masks with k ones { for each of the subsets, generate mst using them + all normal edges use the best possible mst }
I'm getting TLE on one test case. This is O((n k)*(E*logE), E being the number of Edges used for each mst, which is probably too much for n=20 k=10, for exeample.
Does your solution get it in (n k)*n² ? The n on n² being the park edges?
If yes, how? Please help!
How does your solution produce the answer for the Sample Input 1 as given in the PDF ??
В названии тренировки указан 2010 год вместо 2000 — так задумано, или все же?..
Была опечатка, спасибо, исправил.
А кто как задачу I решал?
Наше решение такое: переберем у многоугольника самую левую точку, из всех таких — самую верхнюю Будем называть эту точку стартовой. Далее будем рассматривать только те точки, которые правее. Отсортируем рассматриваемые точки по полярному углу относительно стартовой. Далее следующая динамика: d[start][x][y], где start — наша стартовая точка, x — предпоследняя из точек многоугольника, взятая нами в ответ, y — последняя точка. Переходы: рассматриваем все точки, которые в отсортированном порядке идут ниже y. Пусть мы собираемся добавить в наш многоугольник точку t(иными словами, перейти в состояние d[start][y][t]). Тогда мы должны проверить что поворот xyt — правый, а так же что в треугольнике start-y-t нет синих точек(это делается предподсчетом — какие треугольники у нас "хорошие"). Итоговая асимптотика очевидно n^4 с достаточно маленькой константой.