441A - Valera and Antique Items
Problem author gridnevvvit
You need to implement what written in statement. You could act like that: let's calculate qi — minimum item price from seller i. Then if qi < v, we can make a deal with seller i, otherwise we can't.
Jury's solution: 6850474
441B - Valera and Fruits
Problem author gridnevvvit
Let's start counting days from 1 to 3001. Let current day be i. Additionally, we'll have cur variable — number of fruit we didn't collect previous days. Suppose now fruit is ripen current day. If now + cur ≤ v, we need to add now + cur to answer and update cur value (cur = 0). Otherwise we add v to answer, but cur value need to be updated as follows. Let tv = max(v - cur, 0). Then cur = now - tv. In other words, we try to collect fruits that will not be collectable next day.
Additionally, problem could be solved with  , but this is not required.
, but this is not required.
Jury's solution: 6850502
Bonus. Suppose fruit can be collected at days ai, ai + 1, ..., ai + Ti, where Ti — some number for each tree. How to solve this task optimally?
Additionaly, for every day there will be its own v (maximum number of fruit collected).
441C - Valera and Tubes
Problem author gridnevvvit
The solution is pretty simple. First we need to make such route that visits every cell exactly one time. It is not difficult:
- Initially we stay in (1, 1) cell. Moving from left to right, we should reach (1, m) cell.
- Move to the next line, in (2, m) cell. Moving from right to left, we should reach the most left sell of 2nd line, (2, 1).
- Move to the next line. Repeat 1. and 2. while we have not all cells visited.
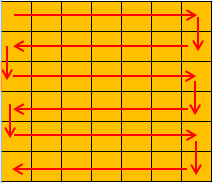
After that, we can easily find the solution: you can make first (k - 1) tubes length be 2, and the last k tube will consist from cells left.
Jury's solution: 6850508
441D - Valera and Swaps
Problem author danilka.pro
In this task you should represent permutation as graph with n vertexes, and from every vertex i exists exactly one edge to vertex p[i]. It's easy to understand that such graph consists of simple cycles only.
If we make swap (i, j), edges 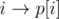 and
and 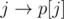 will become edges
will become edges 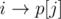 and
and 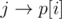 respectively. Then if i and j is in the same cycle, this cycle will break:
respectively. Then if i and j is in the same cycle, this cycle will break:
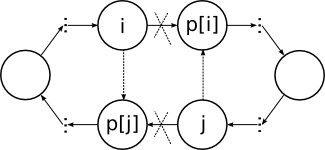
but if they are in different cycles, these cycles will merge into one:
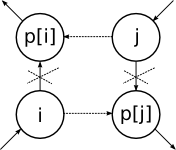
this means that every swap operation increases number of cycles by one, or decreases it by one.
Assuming all above, to get permutation q from permutation p, we need to increase (or decrease) number of cycles in p to n - m. Let c — number of cycles in p. Then k always equals |(n - m) - c|.
For satisfying lexicographical minimality we will review three cases:
1) n - m < c
It's easy to understand, that in this case you must decrease cycles number by merging cycles one by one with cycle containing vertex 1. This way every swap has form (1, v), where v > 1. Because every cycle vertex is bigger than previous cycle vertex, this case can be solved with O(n).
2) n - m > c
In this case you should break cycle for every vertex, making swap with smallest possible vertex (it should be in this cycle too). This could be done if represent cycle by line 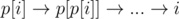 . As soon as every cycle is broken with linear asymptotics, this case solution works with O(n2).
. As soon as every cycle is broken with linear asymptotics, this case solution works with O(n2).
Bonus: this way of representing cycle lets us optimize solution to  asymptotics, you may think how.
asymptotics, you may think how.
3) n - m = с
Besause in this case k = 0, there is nothing need to be swapped.
It's highly recommended to inspect jury's solution: 6850515
441E - Valera and Number
Problem author gridnevvvit
We will solve the task by calculating dynamic d[i][mask][last][cnt] — possibility of getting v which 8 last bits equals mask, 9th bit equals last, cnt — number of consecutive bits (following 9th bit) and equal to last, after i steps.
Good, but why we left other bits? It's clear, that using operation + = 1 we can change only first 0 bit with index ≥ 9.
Transitions is pretty obvious: we add 1 or multiply by 2 (it's recommended to see them in jury's solution). Perhaps, you should ask following question. For example, we have number x = 1011111111 in binary representation.
And at this moment, we make + = 1. According to all above, we must go to d[1][0][1][2] condition, but we can't do that because we don't have any information about 1 in 10th position. But, as we can not change any bit with index ≥ 9 (mask = 0) we make transition to d[1][0][1][1].
Jury's solution: 6850523
Bonus. Let us have other pseudocode.
// input x, k, p
for(i = 0; i < k; i += 1) {
if (x is even) {
rnd = random number from interval [1, 100]
if (rnd <= p)
x *= 2;
else
x += 1;
} else {
x *= 2;
}
}
s = 0;
while (x is even) {
x /= 2;
s += 1;
}
As before, you must find expected value of s.
How effectively you can solve this problem? Can you prove your solution?
Your corrections of my bad English are welcome, thank you.










When will the eng for div2 d, e come out?
When will english translations be available?
I think the google translation is not — so — bad, so you can try it out!
Now.
In problem E editorial, what is 'v' (mentioned in first line)? I would also like to know how you arrived at the DP state you described. Thanks!
v — is some number, which satisfy this pattern (mask, last, cnt).
Because number of operation is small ( ≤ 200) then we can understand, that only last 8 can be changed by adding operations (and first zero bit with index ≥ 9). So, after that we will have such dp states
Can you please give example of how the states are represented by dp[i][mask][last][cnt]?
Sorry,I just press the wrong button.I just want to ask,as there are so many states,will it TLE?Is the transfrom O(1)?
How an easy solution for C!!! I wrote a complex code to do this task, and finally it was failed on system test :(
It's not the first time for me doing this mistake, any suggestion? any trick? How can I think about problems in the easier manner?
Sorry, but I don't understand well dans' explanation about problem D, why always do we need to increase (or decrease) number of cycles in p to n - m?....... What about if we have only a cycle with length m + 1, could be that q? can anyone explain that?
Because to break a cycle into 1-length cycles with length l you need l - 1 swaps. Then to break all the cycles you need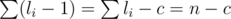 swaps. c is number of cycles in p.
swaps. c is number of cycles in p.
Problem D-
how output of
3
2 3 1
0
is
2
1 2 1 3
this will happen with above ans (231) -> (132) -> (312) but final state should be (123)
EDIT: I got it. swap is operated on index. my mistake.
I am unable to understand how the graph is used for representing the permutation,can anyone help me??If there exist a only 1 edge from i to p[i], then how cycles are formed??
This image shows graph representation of permutation 3 4 5 2 1.
okay got it,thanks
can aNybody plz explAin problem E, this type of problem is completely new for me or link to some tutorial?
Problem E could be solved using dynamic programming method. It is very common, so the better way is to inspect others solutions. Even this task could be solved using DP in different ways. If you are completely new to DP, you can read Wikipedia, inspect posts on Codeforces, or simply use google for it.
Hi guys,
I've seen others' dp solutions such as 6963686 that have used way easier dp solutions than the one in the analysis (this solution uses only 2 dimensions for the dp). Does anyone know an explanation to their solutions? I've read them really throughly and don't quite understand them. Thanks everyone for their help!
dp[i][j]— answer for x + j if we have i operations left.Im sorry i can't understand what variable m stands for,
can someone please explain it to me ??
Seems, that in problem C and problem D m is variable from the input.
There is a similar problem to problem D
"Silly Sort" SPOJ SSORT / 2481 Live Archive / 2002 World Finals ACM
I solved it with the same idea for problem D. The property of that every swap increase or decrease the number of cycles in a permutation(see graph in tutorial) is very useful.
Links:
SSORT
Well, these problems are not similar. They use similar idea, but greedy algorithms are different.
I don't refer for greedy algorithm , in fact i explain in my comment about idea of (that every swap increase or decrease the number of cycles in the graph by one)
This is the similar.
I think this is really a great contest especially the problem D and E.I have never seen these problems and I have learnt a lot from these problems.
The case 2 of 441D - Valera and Swaps can be solved in O(N) using stack
Note that the numbers you choose to swap with the same i are always increasing
We can interate through p[i] → p[p[i]] → ... with a stack to maintain a lexicographical-smallest increasing sub-ring
When you pop some elements, you remove a monotonic sub-ring from the current ring, and thus the order to swap for the sub-ring is certian
Just store them, you dont have to recaculate them
Total time complexity: O(N)
See my code 22617043 for details
Amazing!!! XD
We can do div2 problem B in O(n) too!! solution: 65319642
Why problem D has tag "string suffix structures"?