A. Сначала считаем имена всех членов экипажа и их их статусы в массив. Затем за 4 прохода по массиву выведем сначала имена всех крыс (первый проход), затем имена всех женщин и детей (второй проход), затем имена всех мужчин (третий проход) и, наконец, за четвертый проход выведем имя капитана.
B. В этой задаче нужно было моделировать тренировки до тех пор, пока все солдаты не повысят свой ранг до максимума. Смоделировать одну тренировку можно было с помощью одного прохода по массиву, добавляя единицу ранга последнему солдату в каждой группе солдат одинакового ранга (если его ранг, конечно же, не равен k). Это сохранит неубывающий порядок званий. Очевидно, что для выполнения задачи требуется не более чем kn повышений. Отсюда - сложность предложенного алгоритма O(kn2), что укладывается в ограничения.
На самом деле можно доказать, что повышений будет не более чем n + k, поэтому сложность предложенного выше алгоритма O(n(n + k)). Кроме того, существует простое решение за время O(n).
C. В этой задаче нужно было просто перебрать все возможные числа, которые мог загадать ведущий, а затем проверить, удовлетворяет ли это число всем ответам ведущего на пробные числа отгадывающего. Если таких чисел ровно одно, то следовало вывести это число. Если подходило несколько чисел - нужно было вывести "Need more data". "Incorrect data" следовало вывести в случае, если ни одно из возможных чисел не подходило. Сложность решения O(104 × n)
Возможные ошибки в данной задаче были связаны с ведущим нулем. Иногда он не выводился в ответ, а иногда он не выводился немного раньше - при переводе числа в строку для проверки на то, что оно могло быть загадано ведущим.
D. Главная идея решения - обойти все ячейки острова "змейкой". Это можно было сделать, например, так:
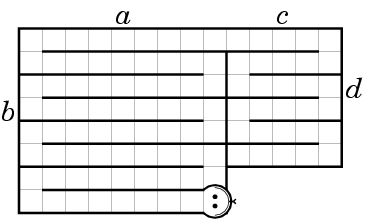
или даже так:
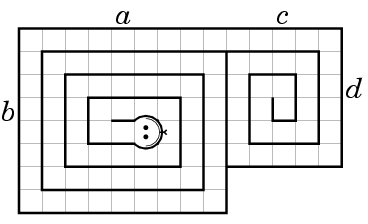
Далее нужно просто обойти эту змейку от головы до хвоста и жадно распределить ячейки между партиями. Понятно, что каждая область, принадлежащая какой либо партии, получится связной.
Сложность решения O(max(B, D) × (A + C)).
E. Назовем состоянием игры некоторое расположение конфет в коробке. Для каждого состояние определим - выигрышное оно или проигрышное. Состояние выигрышное, если у игрока, начинающего игру с этого состояния, существует выигрышная стратегия. Если такой стратегии не существует, то состояние проигрышное.
Делая ход в текущем состоянии, мы попадаем в некоторое другое состояние. Если существует ход, ведущий к проигрышному состоянию, то текущее состояние является выигрышным (игрок, попавший в такое состояние, должен сделать ход в это проигрышное состояние). Если все допустимые ходы ведут в выигрышные состояния, то текущее состояние является проигрышным.
Для решения задачи нужно просто определить выигрышно ли состояние, которое дается во входных данных. Если оно вымгрышно - то торт получает Карлсон, иначе - Малыш. В частности, состояние, когда все ячейки коробки пусты проигрышное.
Каждому состояния удобно сопоставить двоичную маску длины 19. i-ый бит маски равен 1, если в i-ой ячейке коробки лежит конфета, иначе i-ый бит маски равен 0. Для всевозможных ходов так же следует завести массив масок, в которых 1 будет означать, что данную конфету мы съедаем, а 0 - ничего не трогаем.
Теперь проходимся по всем маскам в порядке увеличения и пробуем делать ходы. Для состояния с маской mask ход move допустим тогда и только тогда, когда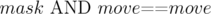 . Допустимый ход же ведет в маску
. Допустимый ход же ведет в маску 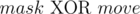 . Заметим, что ходы всегда ведут в маски, которые меньше текущей. Поэтому для тех масок гарантированно будет корректно определено выигрышное состояние или нет.
. Заметим, что ходы всегда ведут в маски, которые меньше текущей. Поэтому для тех масок гарантированно будет корректно определено выигрышное состояние или нет.
Предложенное решение работает за время O(219k), где k - количество всевозможных ходов (их ровно 103).
B. В этой задаче нужно было моделировать тренировки до тех пор, пока все солдаты не повысят свой ранг до максимума. Смоделировать одну тренировку можно было с помощью одного прохода по массиву, добавляя единицу ранга последнему солдату в каждой группе солдат одинакового ранга (если его ранг, конечно же, не равен k). Это сохранит неубывающий порядок званий. Очевидно, что для выполнения задачи требуется не более чем kn повышений. Отсюда - сложность предложенного алгоритма O(kn2), что укладывается в ограничения.
На самом деле можно доказать, что повышений будет не более чем n + k, поэтому сложность предложенного выше алгоритма O(n(n + k)). Кроме того, существует простое решение за время O(n).
C. В этой задаче нужно было просто перебрать все возможные числа, которые мог загадать ведущий, а затем проверить, удовлетворяет ли это число всем ответам ведущего на пробные числа отгадывающего. Если таких чисел ровно одно, то следовало вывести это число. Если подходило несколько чисел - нужно было вывести "Need more data". "Incorrect data" следовало вывести в случае, если ни одно из возможных чисел не подходило. Сложность решения O(104 × n)
Возможные ошибки в данной задаче были связаны с ведущим нулем. Иногда он не выводился в ответ, а иногда он не выводился немного раньше - при переводе числа в строку для проверки на то, что оно могло быть загадано ведущим.
D. Главная идея решения - обойти все ячейки острова "змейкой". Это можно было сделать, например, так:

или даже так:

Далее нужно просто обойти эту змейку от головы до хвоста и жадно распределить ячейки между партиями. Понятно, что каждая область, принадлежащая какой либо партии, получится связной.
Сложность решения O(max(B, D) × (A + C)).
E. Назовем состоянием игры некоторое расположение конфет в коробке. Для каждого состояние определим - выигрышное оно или проигрышное. Состояние выигрышное, если у игрока, начинающего игру с этого состояния, существует выигрышная стратегия. Если такой стратегии не существует, то состояние проигрышное.
Делая ход в текущем состоянии, мы попадаем в некоторое другое состояние. Если существует ход, ведущий к проигрышному состоянию, то текущее состояние является выигрышным (игрок, попавший в такое состояние, должен сделать ход в это проигрышное состояние). Если все допустимые ходы ведут в выигрышные состояния, то текущее состояние является проигрышным.
Для решения задачи нужно просто определить выигрышно ли состояние, которое дается во входных данных. Если оно вымгрышно - то торт получает Карлсон, иначе - Малыш. В частности, состояние, когда все ячейки коробки пусты проигрышное.
Каждому состояния удобно сопоставить двоичную маску длины 19. i-ый бит маски равен 1, если в i-ой ячейке коробки лежит конфета, иначе i-ый бит маски равен 0. Для всевозможных ходов так же следует завести массив масок, в которых 1 будет означать, что данную конфету мы съедаем, а 0 - ничего не трогаем.
Теперь проходимся по всем маскам в порядке увеличения и пробуем делать ходы. Для состояния с маской mask ход move допустим тогда и только тогда, когда
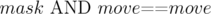 . Допустимый ход же ведет в маску
. Допустимый ход же ведет в маску 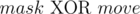 . Заметим, что ходы всегда ведут в маски, которые меньше текущей. Поэтому для тех масок гарантированно будет корректно определено выигрышное состояние или нет.
. Заметим, что ходы всегда ведут в маски, которые меньше текущей. Поэтому для тех масок гарантированно будет корректно определено выигрышное состояние или нет.Предложенное решение работает за время O(219k), где k - количество всевозможных ходов (их ровно 103).











Последняя задача O(219*100), кажется слишком много.
Интересно сколько времени занимает в среднем ?
Также есть решения на Java, работающие до 0.5 с.
я просто для каждой из линий записал позиции и проверял каждый ход за O(leni) где leni - это длина отрезка съедаемых конфет.
При запихивании ходов в маску время работы сокращается раза в 3-4.Спасибо за идею.