488A - Giga Tower
The answer b is very small (usually no larger than 10), because one of a + 1, a + 2, ..., a + 10 has its last digit be 8.
However, b can exceed 10 when a is negative and close to 0. The worst case is a = - 8, where b = 16.
Anyway b is rather small, so we can simply try b from 1, and check whether a + b has a digit 8.
488B - Candy Boxes
Let's sort the four numbers in ascending order: a, b, c, d (where x1, x2, x3, x4 are used in problem statement). So 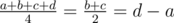 .
.
With some basic math, we can get a: d = 1: 3 and a + d = b + c.
Solution 1:
If n = 0, just output any answer (such as {1, 1, 3, 3}). If n = 1, just output {x, x, 3x, 3x}, where x is the known number. If n = 4, just check whether the four known numbers meet the condition.
If n = 2, let x, y denote the known numbers (x ≤ y). No solution exists if 3x < y. Otherwise we can construct a solution {x, y, 4x - y, 3x} (certainly other solutions may exist).
If n = 3, let x, y, z denote the known numbers (x ≤ y ≤ z). No solution exists if 3x < z. Otherwise the solution can only be {x, y, z, 3x}, 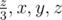 or {x, y, x + z - y, z}.
or {x, y, x + z - y, z}.
Solution 2:
The known numbers are no larger than 500, so all numbers are no larger than 1500 if solution exists. We enumerate x from 1 to 500, y from x to 3x, then {x, y, 4x - y, 3x} is a solution. For each solution, check if it matches the known numbers.
Solution 3:
If n = 0, just output any answer (such as {1, 1, 3, 3}). If n = 1, just output {x, x, 3x, 3x}, where x is the known number. If n = 4, just check whether the four known numbers meet the condition.
Otherwise, we can enumerate the 1 or 2 missing number(s), and check if the four numbers meet the condition.
487A - Fight the Monster
It is no use to make Yang's ATK > HP_M + DEF_M (Yang already can beat it in a second). And it's no use to make Yang's DEF > ATK_M (it cannot deal any damage to him).
As a result, Yang's final ATK will not exceed 200, and final DEF will not exceed 100. So just enumerate final ATK from ATK_Y to 200, final DEF from DEF_Y to 100.
With final ATK and DEF known, you can calculate how long the battle will last, then calculate HP loss. You can easily find the gold you spend, and then find the optimal answer.
487B - Strip
We can use dynamic programming to solve this problem.
Let f[i] denote the minimal number of pieces that the first i numbers can be split into. g[i] denote the maximal length of substrip whose right border is i(included) and it satisfy the condition.
Then f[i] = min(f[k]) + 1, where i - g[i] ≤ k ≤ i - l.
We can use monotonic queue to calculate g[i] and f[i]. And this can be implemented in O(n)
We can also use sparse table or segment tree to solve the problem, the time complexity is  or
or  (It should be well-implemented).
(It should be well-implemented).
For more details about monotonic queue, you can see here
487C - Prefix Product Sequence
The answer is YES if and only if n is a prime or n = 1 or n = 4.
First we can find 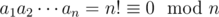 . If n occurs in {a_1,…,a_{n-1}} in the prefix product sequence 0 will occur twice which do not satisfy the condition.
. If n occurs in {a_1,…,a_{n-1}} in the prefix product sequence 0 will occur twice which do not satisfy the condition.
So an must be 0 from which we know a1a2... an - 1 = (n - 1)!. But for any composite number n > 4 we have 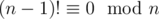 (See the proof below). So we can know that for all composite number n > 4 the answer is NO.
(See the proof below). So we can know that for all composite number n > 4 the answer is NO.
For n = 1, 1 is a solution.
For n = 4, 1, 3, 2, 4 is a solution.
For any prime number n, let ai be 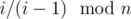 . If there are two same number ai, aj. Then we get i / (i - 1) ≡ j / (j - 1) which leads to i ≡ j, which is a contradiction. So all n numbers will occur exactly once. And this is a solution.
. If there are two same number ai, aj. Then we get i / (i - 1) ≡ j / (j - 1) which leads to i ≡ j, which is a contradiction. So all n numbers will occur exactly once. And this is a solution.
Also, we can find a primitive root g of n and $g^{0}, g^{1}, g^{n-3}, g^{3}, g^{n-5}, \cdots } is also a solution.
Proof:
For a composite number n > 4 it can either be written as the products of two numbers p, q > 1.
If p ≠ q, then we immediately get pq|(n - 1)!.
If p = q, note that n > 4 so 2p < n, we have p2|(n - 1)!
So n|(n - 1)! always holds which means 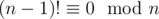
487D - Conveyor Belts
This problem can be solved by classic data structures.
For example, let's try something like SQRT-decomposition. Let's divide the map horizontally into some blocks. For each grid, calculate its destination when going out the current block (or infinite loop before going out current block).
For each modification, recalculate the affected block by brute force. For each query, we can just use the "destination when going out the current block" to speed up simulation.
Let S be the size of a block, then the time for each modification is O(S), for each query is O(nm / S), since at most O(nm / S) blocks, and at most 1 grid of each block are visited.
The total time complexity is O(nm + qnm / S + pS), where p is the number of modifications. Let 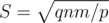 , the complexity can be the best:
, the complexity can be the best: 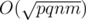 .
.
This task can also be solve by segment tree. The time complexity is 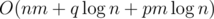 , or
, or 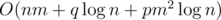 , depending on implementation.
, depending on implementation.
487E - Tourists
First we can find out all cut vertices and biconnected components(BCC) by Tarjan’s Algorithm. And it must form a tree.
From the lemma below, we know that if we can pass by a BCC, then we can always pass any point in the BCC.
We use a priority queue for each BCC to maintain the minimal price in the component.
For each modification, if the vertex is a cut vertex, then modify itself and its related BCCs’ priority queue. If not, modify the priority queue of its BCC.
For each query, the answer is the minimal price on the path from x (or its BCC) to y (or its BCC). We can use Link-Cut Trees or Heavy-Light Decomposition with Segment Trees.
To be more exact, we can only modify the father BCC of the cut vertex in order to guarantee complexity(otherwise it would be hacked by a star graph).When querying, if the LCA of x and y is a BCC. Then the father of the LCA(which is a cut vertex related to the BCC) should also be taken into account.
The time complexity is 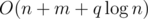 or
or 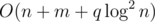 .
.
Lemma: In a biconnected graph with n ≥ 3 points, for any three different vertices a, b, c, there is a simple path to from a to b going through c.
Proof: Consider a biconnected graph with at least 3 vertices. If we remove any vertex or any edge, the graph is still connected.
We build a network on the graph. Let's use (u,v,w) to describe a directed edge from u to v with capacity w. For each edge (u,v) of the original graph, we build (u,v,1) and (v,u,1). Build (S,c,2), (a,T,1) and (b,T,1). For each vertex other than S,T,c, we should give a capacity of 1 to the vertex.
In order to give capacity to vertex u, we build two vertices u1,u2 instead of u. For each (v,u,w), build (v,u1,w). For each (u,v,w), build(u2,v,w). Finally build (u1,u2,1).
Hence, if the maximal flow from S to T is 2, there is a simple path from a to b going through c.
Now we consider the minimal cut of the network. It is easy to find that minimal cut <= 2, so let's prove minimal cut > 1, which means, no matter which edge of capacity 1 we cut, there is still a path from S to T.
If we cut an edge like (u1,u2,1), it is equivalent to set the capacity of the vertex to 0, and equivalent to remove the vertex from the original graph. The graph is still connected, so there is still a path in the network.
If we cut other edges, it is equivalent to remove an edge from the original graph. It is still connected, too.
Now we have minimal cut > 1, which means maximal flow = minimal cut = 2. So there is always a simple path from a to b going through c.











Ouch no wonder the guy that solved E didn't solve anything else in the contest >.>
Btw with the current constraints (10000 change queries) can be solved using SQRT decomposition on queries in the general case (any table size, <>^v symbols).
I'm getting TL#23 in E.. what's so special about this test? All other tests run in under 200ms. 8828242
Test 23 is a star-shaped graph. Some types of implementation will get bad time complexity here.
I'm using heavy-light decomposition, which should be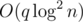 (adding cut vertices to the parent component as suggested). I tested on a simple star graph and it also works very quickly.
(adding cut vertices to the parent component as suggested). I tested on a simple star graph and it also works very quickly.
For test 23, most queries are about the centre of the star. Besides there's really nothing special.
Fixed some bugs, now TL 24 >.> Upd: finally! 8837715
Thanks! Спасибо!
What happened to all comments here? Was that blog entry deleted and uploaded once again?
Seems so, the link in the main contest entry doesn't work.
Could you post your comment about solution with segment tree for problem D once again?
Ugh, I don't like writing the same thing twice, because of technical issues :P. In short: Let information about what happens if you start in rows interval [l, r] for all possible starting position (r, i) be denoted as I(l, r) (it's a set of m pairs of ints). Key observation is that if you know I(a, b) and I(b + 1, c), then you also know I(a, c), what lets you do some segtreeing.
Thanks, I'll try code it tomorrow :)
Can I get some clarification on why i/(i-1) % n == j/(j-1) % n, clearly tells i==j. It doesn't seems that straightforward to me?
Cheers.
What to do with cutpoints in E.div1 ?
Since you also PMed me about this, I'll just post my solution here so everyone can see.
First, we use standard algorithms (DFS) to find the cut vertices and biconnected components of the graph. Now, we build a tree out of these biconnected components as follows: Let the vertices of the tree represent each cut vertex and each biconnected component and draw edges between each cut vertex and every biconnected component that the vertex is in. The tree allows us to restate the queries as "find the minimum value on the path from u to v", where u and v are the tree vertices corresponding to the vertices in the original query. This can be solved by finding the minimum value from u to lca(u, v) and from v to lca(u, v).
However, our situation is slightly more complex, since when we update the value of a cut vertex, we have to update the values of all the biconnected components around it, which can take up to O(n) time (when the tree is a star-shaped graph as shigule mentioned above). We get around this issue by having each biconnected component only contain the values of its children. Thus when we ask for the minimum value in a biconnected component, we also have to check the value of its parent (which is another cut vertex). In addition, this means that when we update each cut vertex, we have to update the value of its parent as well. Essentially, what we're doing is using the structure of the tree to make some of the updating "lazier", taking the number of updates in the worst case from O(n) to O(1).
Implementing a link-cut tree to do all of these operations (path-minimum and vertex updates) is pretty standard — the only unusual part is that each biconnected component vertex actually represents a multiset, where the multiset contains the values of (almost) all the vertices in its biconnected component.
Can someone please provide the explanation to solve 487B — Strip using Sparse Table and Segment Tree?
For any prime number n, let ai be i/(i-1) mod n.How is that found out or assumed? Cannot understand. Please explain.
If ai = i/(i-1) mod n, then a1*a2*...*ai = i mod n. an = n mod n = 0. It's easy to see that [1, 2, ... n-1, 0] is a permutation of [0, 1, ... , n-1].
Thanks.
For the problem "Strip" (Div2 — D), could anyone put up their solution which solves the problem using sliding window minimum? I have calculated 'g' (as described in the editorial) using a similar approach, but I can't figure out how to calculate the array 'f' using this concept.
g[i + 1] < = g[i] + 1 so it's also a sliding window minimum problem.
You can see vfleaking's solution 8781576 for details.
Hello! Is that test is try? (Problemset 488A)
The number '-80000000' is already lucky, so answer = 1. Isn't it?
---------------------------------------------------------- 23
Ввод
-80000000
Вывод участника
1
Ответ жюри
2
Комментарий чекера
wrong answer 1st numbers differ — expected: '2', found: '1'
If he walks a floor higher, he will arrive floor
-79999999NOT-80000001In problem 487B — Strip why
f[i] = min(f[k]) + 1, where i - g[i] ≤ k ≤ i - l.?Please give the segment tree approach for 487B - Strip ?
https://mirror.codeforces.com/contest/487/submission/98249638
I have a very different solution for 487B-Strip.
We can actually store the intervals (which must necessarily have one boundary) and then greedily try to put a boundary in the interval. If we are successful in doing so, then we return the number of boundaries+1, otherwise return -1.
The code is really simple. (Also, I have added lots of comments to supplement the code)
:)