Each problem comes with a challenge — a bonus task somehow related to the problem; you may tackle at the challenges for fun and practice, also feel free to discuss them at the comments. =)

496A - Minimum Difficulty

For every option of removing an element we run through the remaining elements and find the maximal difference between adjacent ones; print the smallest found answer. The solution has complexity O(n²). It can be noticed that after removing an element the difficulty either stays the same or becomes equal to the difference between the neighbours of the removed element (whatever is larger); thus, the difficulty for every option of removing an element can be found in O(1), for the total complexity of O(n). Any of these solutions (or even less efficient ones) could pass the tests.

Challenge: suppose we now have to remove exactly k arbitrary elements (but the first and the last elements have to stay in their places). How small the maximal difference between adjacent elements can become? Solve this problem assuming the limitations are as follows: 1 ≤ k ≤ n - 2, n ≤ 10⁵, a_i ≤ 10⁹.

496B - Secret Combination

We observe that the order of operations is not important: we may first perform all the shifts, and after that all the additions. Note that after n shifts the sequence returns to its original state, therefore it is sufficient to consider only the options with less than n shifts. Also, after 10 times of adding 1 to all digits the sequence does not change; we may consider only options with less than 10 additions. Thus, there are overall 10n reasonable options for performing the operations; for every option perform the operations and find the smallest answer among all the options. As performing the operations for every option and comparing two answers to choose the best takes O(n) operations, this solution performs about 10n² elementary operations. The multiple of 10 can be get rid of, if we note that after all shifts are made the best choice is to make the first digit equal to zero, and this leaves us but a single option for the number of additions. However, implementing this optimization is not necessary to get accepted.

Challenge: can you solve the problem in time? in O(n) time?

496C - Removing Columns/497A - Removing Columns

Let's look at the first column of the table. If its letters are not sorted alphabetically, then in any valid choice of removing some columns it has to be removed. However, if its letters are sorted, then for every valid choice that has this column removed it can be restored back to the table; it is clear that the new choice is valid (that is, the rows of the new table are sorted lexicographically) and the answer (that is, the number of removed columns) has just became smaller.

Consider all columns from left to right. We have already chosen which columns to remove among all the columns to the left of the current one; if leaving the current column in place breaks the lexicographical order of rows, then we have to remove it; otherwise, we may leave it in place to no harm. Arguing in the way of the previous paragraph we can prove that this greedy method yields an optimal (moreover, the only optimal) solution. The complexity is O(n²).

Challenge: compute how many (say, modulo 10⁹ + 7) n × m tables are there for which the answer for this problem is k? The more efficient solution you come up with, the better.

496D - Tennis Game/497B - Tennis Game

Choose some t; now emulate how the match will go, ensure that the record is valid for this t and by the way find the corresponding value of s. Print all valid options for s and t. This solution works in O(n²) time, which is not good enough, but we will try to optimize it.

Suppose the current set if finished and we have processed k serves by now. Let us process the next set as follows: find t-th 1 and t-th 2 after position k. If t-th 1 occurs earlier, then the first player wins the set, and the set concludes right after the t-th 1; the other case is handled symmetrically. If the match is not over yet, and in the rest of the record there are no t ones nor t twos, then the record is clearly invalid. This way, every single set in the record can be processed in time using binary search, or O(1) time using precomputed arrays of positions for each player.

Now observe that for any t a match of n serves can not contain more than n / t sets, as each set contains at least t serves. If we sum up the upper limits for the number of sets for each t, we obtain the total upper limit for the number of sets we may need to process: 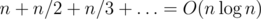(which is the famous harmonic sum). Using one of the approaches discussed above, one obtains a solution with complexity of or ; each of these solutions fits the limit nicely.

Obviously, for every t there is no more than one valid choice for s; however, maybe a bit unexpected, for a given s there may exist more than one valid choice of t. The first test where this takes place is pretest 12. The statement requires that the pairs are printed lexicographically ordered; it is possible to make a mistake here and print the pairs with equal s by descending t (if we fill the array by increasing t and then simply reverse the array).

Challenge: while preparing this problem I discovered that it's quite hard to find a test such that the number of pairs in the answer is large; in the actual tests the maximal number is 128, which is the number of divisors of the number 83160. Can you beat this record? If you have a test with n ≤ 10⁵ that has larger number of pairs in the answer, feel free to brag in the comments; also don't hesitate to share any insights on how one could bound the maximal number analytically.

496E - Distributing Parts /497C - Distributing Parts

Sort all the parts and actors altogether by increasing lower bounds (if equal, actors precede parts); process all the enitities in this order. We maintain a set of actors which have already occured in the order; if we meet an entry for an actor, add it to the set. If we currently process a part, we have to assign it to an actor; from the current set of actors we have to choose one such that his d_i ≥ b_j (the c_i ≤ a_j constraint is provided by the fact that the i-th actor has occured earlier than the j-th part); if there are no such actors in the set, no answer can be obtained; if there are several actors satisftying this requirement, we should choose one with minimal d_i (intuitively, he will be less useful in the future). Assign the chosen actor with the current part and decrement his k_i; if k_i is now zero, the actor can not be used anymore, thus we remove him from the set.

To fit the limits we should implement the set of current actors as some efficient data structure (e.g., an std::set or a treap). The resulting complexity is .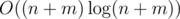

Challenge: suppose that now there are q_j copies of the j-th part (1 ≤ q_j ≤ 10⁹), and each copy must be separately assigned with an actor in a valid way. Can you solve this new problem with all the old constraints (as the actual distribution now has too much entries, it is sufficient to check whether an answer exists)?

497D - Gears

When a collision happens, a vertex of one polygon lands on a side of the other polygon. Consider a reference system such that the polygon A is not moving. In this system the polygon B preserves its orientation (that is, does not rotate), and each of its vertices moves on some circle. Intersect all the circles for vertices of B with all the sides of A; if any of them intersect, then some vertex of B collides with a side of A. Symmetrically, take a reference system associated with B and check whether some vertex of A collides with a side of B. The constraints for the points' coordinates are small enough for a solution with absolute precision to be possible (using built-in integer types).

Another approach (which is, in fact, basically the same) is such: suppose there is a collision in a reference system associated with A. Then the following equality for vectors holds: x + y = z; here z is a vector that starts at P and ends somewhere on the bound of A, x is a vector that starts at Q and ends somewhere on the bound of B, y is a vector that starts at P and ends somewhere on the circle centered at P that passes through Q. Rewrite the equality as y = z - x; now observe that the set of all possible values of z - x forms the Minkowski sum of A and reflection of B (up to some shift), and the set of all possible values of y is a circle with known parameters. The Minkowski sum can be represented as a union of nm parallelograms, each of which is the Minkowski sum of a pair of sides of different polygons; finally, intersect all parallelograms with the circle.

Both solutions have complexity O(nm). As noted above, it is possible to solve the problem using integer arithemetics (that is, with absolute precision); however, the fact that the points' coordinates are small lets most of the solutions with floating point arithmetics pass. It was tempting to write an approximate numerical solution; we struggled hard not to let such solutions pass, and eventually none of them did. =)

Many participants had troubles with pretest 8. It looks as follows (the left spiral revolves around the left point, and the right spiral revolves around the right point):

Challenge: suppose we want a solution that uses floating point arithmetics to fail. In order to do that, we want to construct a test such that the polygons don't collide but pass really close to each other. How small a (positive) distance we can achieve, given the same constraints for the number of points and the points' coordinates?

497E - Subsequences Return

Consider some string; how does one count the number of its distinct subsequences? Let us append symbols to the string consequently and each time count the number of subsequences that were not present before. Let's append a symbol c to a string s; in the string s + c there are as many subsequences that end in c as there were subsequences in s overall. Add all these subsequences to the number of subsequnces of s; now each subsequence is counted once, except for the subsequences that end in c but were already present in s before; these are counted twice. Thus, the total number of subsequences in the new string is twice the total number of subsequences in the old string minus the number of subsequences in the old string which end in c.

This leads us to the following solution: for each symbol c store how many subsequences end in c, denote cnt_c. Append symbol c; now cnt_c becomes equal to the sum of all cnt's plus one (for the empty subsequence), and all the other cnt's do not change.

For example, consider the first few symbols of the Thue-Morse sequence:

• ε — (0, 0)

• 0 — ( 0 + 0 + 1 = 1, 0)

• 01 — (1, 1 + 0 + 1 = 2)

• 011 — (1, 1 + 2 + 1 = 4)

• 0110 — ( 1 + 4 + 1 = 6, 4)

• ...

Let us put the values of cnt in the coordinates of a vector, and also append a coordinate which is always equal to 1. It is now clear that appending a symbol to the string alters the vector as a multiplication by some matrix. Let us assign a matrix for each symbol, and also for each string as a product of matrices for the symbols of the strings in that order.

Now, consider the prefix of the sequence a_i of length k^m. Divide it into k parts of length k^m - 1; x-th (0-based) of these parts can be obtained from the 0-th one by adding x modulo k to all elements of the part. Let us count the matrices (see above) for the prefixes of length k^m, and also for all strings that are obtained by adding x to all of the prefixes' elements; denote such matrix A_m, x.

It is easy to see that if m > 0, then 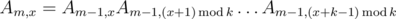. This formula allows us to count A_m, x for all 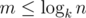and all x from 0 to k - 1 in 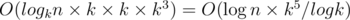time. Now, upon having all A_m, x we can multiply some of them in the right order to obtain the matrix for the prefix of the sequence a_i of length n.

Unfortunately, this is not quite enough as the solution doesn't fit the time limit yet. Here is one way to speed up sufficiently: note that the product in the formula 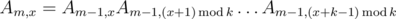can be divided as shown: A_{m - 1, x}... A_{m - 1, k - 1} × A_{m - 1, 0}... A_{m - 1, x - 1} (if x = 0, take the second part to be empty). Count all the "prefixes" and "suffixes" products of the set A_m, x: P_m, x = A_m, 0... A_{m, x - 1}, S_m, x = A_m, x... A_{m, k - 1}. Now A_m, x = S_{m - 1, x}P_{m - 1, x}. Thus, the computation of A_m, x for all x and a given m can be done as computing all P_{m - 1, x}, S_{m - 1, x} using O(k) matrix multiplications, and each A_m, x is now can be found using one matrix multiplication. Finally, the solution now works in 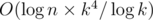time, which fits the limits by a margin.

Challenge: solve the problem for k ≤ 100.