A. Для решения задачи можно было вывести одни из следующих формул:
res = abc - (a - 1)(b - 1)(c - 1), res = ab + bc + ca - a - b - c + 1, или какую любо аналогичную.
Кроме того, задачу можно было решить за O(a + b + c) — аккуратно спускаться от верхнего слоя к нижнему и суммировать общее число плиток.
Автор — Ripatti .
B. Студентов можно представить вершинами некоторого графа, а отношения — ребрами в этом графе. Нам нужно выкинуть как можно меньше вершин, после чего покрасить вершины в 2 цвета так, чтобы любое ребро соединло вершины различных цветов, а вершин разных цветов было поровну.
Нетрудно понять, что граф состоит из цепочек, циклов и отдельных вершин. Каждую из этих компонент можно легко покрасить нужным образом в 2 цвета, кроме одного случая: циклы нечетной длины. Таким образом, для решения задачи необходимо выкинуть по 1 вершине из каждого нечетного цикла. После данной операции у нас может остаться нечетное число вершин — тогда выкинем еще одну. В итоге получим граф из четного числа вершин, состоящий из цепочек, четных циклов и отдельных вершин. Такой граф легко раскрасить нужным способом.
С. Первое решение: разбор случаев.
1. k = 1. Здесь для n ≤ m + 1 нужно 3 сотрудника, а для n > m + 1 — 2 сотрудника, кроме одного хитрого случая: для n = 2, m = 2, k = 1 ответ 4.
2. k > 1. Для n = m ответ 2k + 1, для всех остальных случаев ответ 2k.
Во всех случаях легко построить сами решения, а так же вручную доказать их корректность.
Второе решение: жадность.
Заведем массив достаточно большого размера, в котором будем хранить текущее число работников в каждый из первых несколько дней. Теперь просто будем идти по нему слева направо от 1го для до n + m-го и нанимать работников так, чтобы все было хорошо. А именно: нанимаем работника если в текущий день персонала меньше k или же если в следующий день персонала 0 человек (этот работник нужен чтобы передать ключ).
Можно показать, что это решение работает за O((n + m)k).
Это решение так же работает и для случаев n < m, но за более большую асимптитику.
D. Для каждого сектора отсортируем все перемычки по расстоянию от центра паутины. Теперь для каждого сектора при помощи трех указателей (один для данного сектора, 2 для соседних) посчитаем число плохих ячеек. Собственно, все. Главное не запутаться.
Решение за 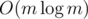 , где m — общее число перемычек.
, где m — общее число перемычек.
Автор — Ripatti .
E. Цифровой корень почти всегда равен самому числу по модулю k - 1. Единственное расхождение для цифровых корней 0 и k - 1 — для них обоих число по модулю k - 1 будет 0. Но цифровой корень 0 мы можем получить только из числа вида 00...00, количество которых можно посчитать отдельно. Отсюда легко понять как вычислить количество подстрок с нужным цифровым корнем, зная число подстрок, равных по модулю некоторому числу.
Теперь давайте поймем как получить число подстрок нужного модуля. Будем идти по строке слева направо и поддерживать для каждого модуля количество префиксов с таким модулем в массиве dp[] размера k. Пусть текущая позиция i. Тогда число подстрок с модулем b, оканчивающихся в позиции i, равно числу префиксов левее позиции i с модулем (x - b)mod(k - 1), где x — модуль подстроки s[1... i]. Т.е. просто dp[(x - b)mod(k - 1)].
Чтобы это решение прошло по времени, массив dp[] следует заменить на какой нибудь ассоциативный массив. Например, на std::map в языке С++ или на хэштаблицу.
Итого решение за O(nz), где z — сложность доступа к массиву ( для std::map или O(1) для хэштаблицы).
для std::map или O(1) для хэштаблицы).
Автор — Ripatti.











Вопрос по задаче В: как понять, что делать, если у нас 2, 3 или больше треугольников имеют общую вершину?
Видимо, так не бывает — благодаря свойству, что у каждого студента не более двух врагов. (Или я не понял о чём вообще речь...)
Точно, спасибо) Как всегда не дочитал условие)
D. Раз уж мы сортировали, то не ухудшая асимптотику можно искать бинпоиском границы в соседних, что вроде проще.
С. Как такая асимптотика получается в жадном решении и почему при n < m она другая, что-то не очень понял
Кажется понял: подразумевается видимо O((n + m) + ans * n) = O(( n +m)k), если просто отмечать что в следующие n дней мы работаем. Если поддерживать очередь концов дней работ вроде бы получается O(n + m + ans) = O(n + m + (n+m)k) всегда и =O(n + m + k) в нашем случае
В C есть общая стратегия: в первый день нанять k работников, далее, пока нужно, в n·t день нанимаем одного, чтобы передал ключ, и в n·t + 1 берём ещё k - 1 человек. Ответ можно за О(1) посчитать. Отдельный случай — k = 1, там совсем просто.
Я тоже за О(1) считал, я понимаю.
Что, не я один не заметил m ≤ n?
Я заметил, но жадину все равно было лень писать ибо понятно как разобрать случаи
Прекрасный тур, задачи были крайне интересны, даже учитывая, что они здесь всегда такие. Хотя я полтора часа и проторчала с D, так и не пройдя на нем все претесты, впечатление осталось приятное. Спасибо составителям за 2 прекрасных часа!
В кой-то веки совсем очевидная E :) Которую я написал только сейчас, надо действительно читать все задачи :(
Как доказать формулы в А?
написать общую формулу в духе k = x(a2 + b2 + c2) + y(ab + bc + ac) + z(a + b + c) + q и быстро подобрать коэффициенты)
Ещё способ — см. http://mirror.codeforces.com/blog/entry/5061?locale=ru#comment-101668 Я делал точно так же, только не посчитал нужным об этом писать...
Это наверное не доказательство, но я выводил формулу так:
Как-то так :)
Например, посмотреть на данный шестиугольник как на сумму трех "прямоугольников".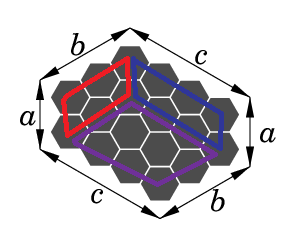
можно посмотреть на эту картинку в 3D, тогда получим 3 грани параллерепипеда. Это то же самое, что параллелепипед размера abc без углового параллелепипеда (a-1)(b-1)(c-1). Отсюда очевидно идет моя 1я формула...
это было
Мне еще во время соревнования показалось, что задача С намного легче задачи В...
Почему никто не применил анти-жаба-квиксорт в D? Судя по беглому анализу решений, осталось бы только 4 АС: 2009123, 2009269, 2010726, 2012646.
Ну у меня используется Collections.sort(), который mergesort.
Ах да, еще 2010322 и 2012499. Я просто забыл про Java 7 :).
Ну тут дело не в Java 7 (Хотя кстати quick sort в Java 7 еще тоже публично не ломали)
Ломали.
А про Java 7 я помянул потому, что просмотрел решения на Java 6, а на Java 7 забыл.
Спасибо за инфу)
Да не за что :).
А ты типа все решение просмотрел?
А их всего 22 штуки.
Их под 300 о_О
Речь про решения на Java :).
А в задаче E можно было HashMap поломать. Правда такой сабмит всего один.
В сообщении, которое я комментировал ни слова про Java..)
А "анти-жаба-квиксорт" — это про что?
Я до теперь не знал, что это за штука. Думал, это квиксорт обычный.
Почему цифровой корень числа почти всегда равен числу по модулю (k-1)?
Мне тоже пришлось немного подумать, чтобы это понять. Пусть дано число ankn + an - 1kn - 1 + ... + a0. Каждый из членов aiki можно представить в виде ai(k - 1 + 1)i. Разложим это по формуле бинома Ньютона и заметим, что каждый член, кроме последнего члена ai·1, даёт остаток 0 по модулю k - 1. Суммируя по всем i, получаем
Продолжая по цепочке, придём к утверждению авторов.
P.S. Почему CF не распознаёт
\pmod? :-/Спасибо, понял.
После разбора узнаем, что d(x) = x % (k-1) (кроме граничных случаев). Ваши выкладки доказывают правоту этого равенства.
Возникает вопрос: Как участники получили это равенство во время контеста? 1) Это известный факт? или 2) Участники имеют прокаченную мат.часть, чтобы выводить такие вещи самостоятельно?
Это известный факт( по крайней мере, для меня), да и доказывается это легко.
Какими тестами ломали по задаче B div2. 2012128 - а то не могу у себя ошибку найти.
Ищи на страничке взломы, твое будет выделено
+1.Спасибо. Минуту назад нашёл. Не сразу сообразил.
Люди, помогите. В задаче В на моем компиляторе (Visual Studio C++ 2010) тесты из примера проходят, отсылаю на проверку через 2005 студию и GNU C++ — Runtime error 1. Что это может быть?
freopen'ы убери, надо использовать stdin/stdout
Благодарю)
Вы где-то вылазите за пределы массива ( я так думаю ). А лучше сделайте ссылку на ваш submit. UPD: разобрались.
in the tutorial for B its said that : "So, you should drop one vertex from every odd cycle. After that you can get odd number of vertices" can we remove vertex arbitrary??? or we should select the vertex that is in maximum number of odd cycles? for example according to the tutorial we can remove any vertex of following graph at first step: my graph: 5 6 1 2 1 3 1 4 1 5 2 3 4 5 if at first step i remove node 2 or 3 or 4 or 5 after that the graph is still non-bipartite so i should remove one more vertex for example 4 or 5 if at first step i removed 2 or 3 then after removing this two node the graph has odd vertexes but if at first step i remove vertex 1 the new graph is bipartite with even number of vertexes! my main question is : shouldnt we remove the vertex that is in maximum number of odd cycles? thanks in advance!
The problem statement says that no vertex has more than two connections. This means that it can't participate in more than one cycle. In this setting, it doesn't matter which one of a cycle's vertices is removed.
hey safecomp I posted here another explanation of problem B, you can take a look it may help.
In the posted solutions here for C I think that there are some mistakes: First solution:
Case 2- k > 1. If n = m, answer is 2k + 1, otherwise answer is 2k. Is it true???? What about n=3 m=9 k=3?? The solution here is 13 != 2*3=6
I think that this case should be: if k > 1 and m > n the answer is: k*(1+ceil(m/n)) + ((m%n==0)?1:0) if k > 1 and n>m the answer is: 2*k
Second solution: I don't understand what does "This solution also works correctly for cases n < m, but then it has bigger complexity and requires more time" means!! I think it has the same complexity no matter n and m
Sorry I didn't notice that!!! But the problem is more interesting if m could be greater than n!! :)
Problem E is similar to http://www.codechef.com/AUG12/problems/LUKYDRIV
Can someone please provide a proof of the result of question A — Tiling with Hexagons ?
do u still want it?
I don't remember the question lol. But sure, go ahead
you can use something like principal of inclusion and exclusion here — break the figure into three pieces with parallelograms of dimns-(a,b),(b,c),(c,a) then individually they can contain ab,bc,ca hexagons respectively . now subtract overcounted hexagons which are a,b,c (intersection of them) but since we also overcounted in subtraction add a 1 at last. hope you understood.
it's awesome thanks
chaluMan explained it well. The other version of the formula, abc-(a-1)(b-1)(c-1) can also be visualised. Dont see the figure as a 2-d floor, but as a 3-d cuboid of height a, breadth b, and length c. This cuboid is made of those hexagonal shaped balls. We have to count the number of balls we are able to "see" from that view. The volume of whole cuboid is abc, so there are that many total balls in it. But we are able to see only the "skin" of the cuboid that is towards us. The skin away from us and the core of the cuboid are unseen. So the balls contained in them must be subtracted. If one visualises properly, dimension of that unseen cuboid are a-1,b-1,c-1, Hence the answer.