NOTE : Knowledge of Binary Indexed Trees is a prerequisite.
Problem Statement
Assume we need to solve the following problem. We have an array, A of length N with only non-negative values. We want to perform the following operations on this array:
Update value at a given position
Compute prefix sum of A upto i, i ≤ N
Search for a prefix sum (something like a
lower_boundin the prefix sums array of A)
Basic Solution
Seeing such a problem we might think of using a Binary Indexed Tree (BIT) and implementing a binary search for type 3 operation. Its easy to see that binary search is possible here because prefix sums array is monotonic (only non-negative values in A).
The only issue with this is that binary search in a BIT has time complexity of O(log2(N)) (other operations can be done in O(log(N))). Even though this is naive, here is how to do it:
Most of the times this would be fast enough (because of small constant of above technique). But if the time limit is very tight, we will need something faster. Also we must note that there are other techniques like segment trees, policy based data structures, treaps, etc. which can perform operation 3 in O(log(N)). But they are harder to implement and have a high constant factor associated with their time complexities due to which they might be even slower than O(log2(N)) of BIT.
Hence we need an efficient searching method in BIT itself.
Efficient Solution
We will make use of binary lifting to achieve O(log(N)) (well I actually do not know if this technique has a name but I am calling it binary lifting because the algorithm is similar to binary lifting in trees using sparse table).
What is binary lifting?
In binary lifting, a value is increased (or lifted) by powers of 2, starting with the highest possible power of 2, 2⌊ log(N)⌋, down to the lowest power, 20.
How binary lifting is used?
We are trying to find pos, which is the position of lower bound of v in prefix sums array, where v is the value we are searching for. So, we initialize pos = 0 and set each bit of pos, from most significant bit to least significant bit. Whenever a bit is set to 1, the value of pos increases (or lifts). While increasing or lifting pos, we make sure that prefix sum till pos should be less than v, for which we maintain the prefix sum and update it whenever we increase or lift pos. See implementation.
It is not very difficult to come up with a rigorous proof of correctness and I am leaving it as an exercise for the readers.
HINT : Each position in bit stores sum of a power of 2 elements, sum of last i& - i (this isolates least significant bit of i) elements till i are stored at position i in bit. I hope this will atleast help you think of an intuitive proof.
Implementation :
// This is equivalent to calculating lower_bound on prefix sums array
// LOGN = log(N)
int bit[N]; // BIT array
int bit_search(int v)
{
int sum = 0;
int pos = 0;
for(int i=LOGN; i>=0; i--)
{
if(pos + (1 << i) < N and sum + bit[pos + (1 << i)] < v)
{
sum += bit[pos + (1 << i)];
pos += (1 << i);
}
}
return pos + 1; // +1 because 'pos' will have position of largest value less than 'v'
}
Example
I am using the example from TopCoder BIT Tutorial, which I recommend you to take a look at if you haven't already (**very important** for understanding this).
Let this be array A,
The BIT for this array will look as follows,
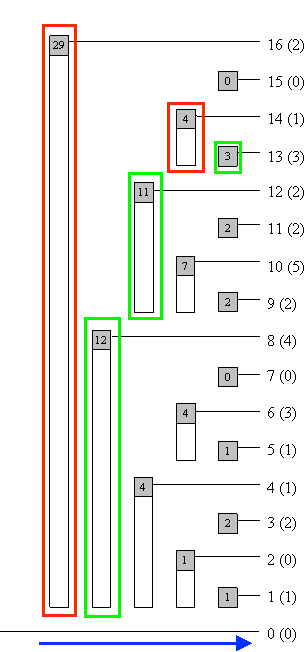
(Illustrations taken from https://www.topcoder.com/community/data-science/data-science-tutorials/binary-indexed-trees/)
Let us assume we want to search for v = 27. The blue arrow shows the direction in which we proceed in our search. Red shows that we can't lift pos. Green shows that we lift pos.
This is how the algorithm proceeds,
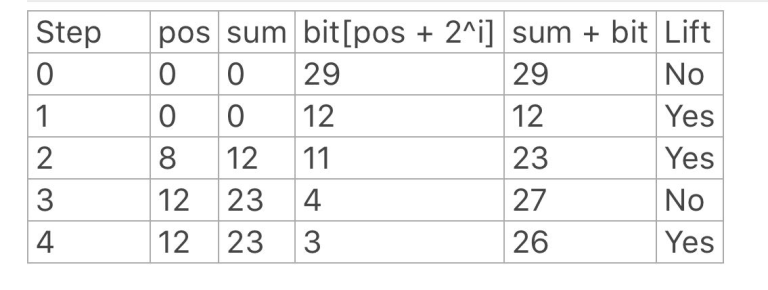
Finally, pos = 13, sum = 26 after last step.
Targetpos = pos + 1 = 14. You can verify that 14 is indeed the lower bound of 27 in prefix sums array!
I hope this helps in understanding the algorithm better. If it is still unclear go through TopCoder BIT Tutorial to understand the structure of BIT so that it can be related to this example.
Taking this forward
You must have noted that proof of correctness of this approach relies on the property of the prefix sums array that it monotonic. This means that this approach can be used for with any operation that maintains the monotonicity of the prefix array, like multiplication of positive numbers, etc.
You can also take a look at a similar blog by adamant.
Thats all folks!
PS : Please let me know if there are any mistakes.
UPDATE : As requested by some people, I have added an example for explain the algorithm.
Auto comment: topic has been updated by sdnr1 (previous revision, new revision, compare).
Link to problem on this technique
It would be nice if you could provide solution to this problem as an example in your blog
Link to actual problem on this technique
Auto comment: topic has been updated by sdnr1 (previous revision, new revision, compare).
This trick is really simple and awesome, thanks for the easy to understand code, I was able to learn the idea purely from the implementation.
This kinda reminds me of segment tree walks, and I find this type of thing (logn instead of binary search) really cool.
Basically here is how I understand it:
1) Greedily (biggest power of 2 first) take the biggest possible position such that prefix_sum[pos] < v. (<= for upper_bound)
2) Add 1 to this position, because prefix_sum[pos+1] >= v. Note that it is impossible for it to be < v, otherwise it wouldn't be greatest position.
3) We can just track the sum by adding bit[pos + (1 << i)] < v because when we are looping in decreasing order the newly added bit will always be the least significant 1 bit, and i & -i actually just gives you the least significant 1 bit.
Hope you all had as much as fun as I did reading this.
starting with the highest possible power of 2, 2⌈ log(N)⌉ , down to the lowest power, 20.
The highest power should be 2⌈ log(N)⌉ - 1. This is because ⌈ log(N)⌉ represents the total number of bits needed to represent a non-negative integer N. But we need to subtract 1 from this number as your power is indexed from 0.
Thanks for pointing out. Although I had noticed it earlier but since we are already checking everytime before we increment
pos, it does not matter even if we start from a higher power, thus did not change it. Anyway I have made a change from ceil to floor (ceil — 1 will miss the last position if N is power of 2).Whenever a bit is set to 1, the value of pos increases (or lifts)
This statement is pretty confusing. You initially defined pos to be the lower bound of v in the prefix sums of array A — this means that, assuming v exists in the prefix sums, prefix_sums[pos] = v. In other words, pos should be a fixed value.
We actually are trying to find the value of
pos. So initially it is 0, and we greedily lift it to the target value. Also it is not necessary that v exists in prefix sums array (similar to how lower_bound works forset).Thanks for pointing out. Fixed it now.
The similar tutorial by adamant
Don't worry bro, all these blogs are basically made for contribution whoring, no other reason.
Blogewoosh too is nothing but translated words of previously existing polish blogs to english and voila, you are now on top of contribution list.
I believe that the desire to share knowledge is also a reason. I don't worry, as I don't think that it's bad that there are several topics on the same theme. Also, the navigation on CF is really bad, I mean sometimes it's hard to find some topic that you have read before, and the reference to adamant's article here may help someone...
Exactly, sometimes it's too hard to find something you've read before, it might be good to have a whole new section on codeforces for tutorials and related stuff, separate from other blogs.
That is true. I did not come across this blog before. When I discovered this technique I wanted to share it. The contribution I am getting is just an added bonus :').
Also, thanks for sharing adamant's blog. I have added the link to the above mentioned tutorial in my blog itself.
I would like to suggest a formal proof for this technique.
I read somewhere that form of binary search is actually called meta binary search.
Given a non-decreasing function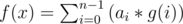
and a target value V where 
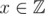and ai is the ith digit in the base 2 representation of x. Meta binary search returns a value, X, whose base 2 representation has exactly n digits and f(X) = V. It should be clear that g(i) must also be non-decreasing for all i. Otherwise, f(x) might not be non-decreasing.
The correctness of meta binary search can be proved the exact same way as that of the classical binary search. In fact, they operate in the same way just that meta binary search is more fancy.
Now, let BIT(i) represent the value stored at index i in a binary-indexed tree/fenwick tree.
Let's assume that BIT(i) is non-decreasing for all i and prove the following lemma:
We want to show that, for all indexes, x, of the actual array,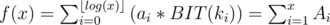
where A represents the actual array and ki is the value that we obtain after the ith iteration of the meta binary search.
Proof by induction:
We shall follow the fenwick tree construction strategy in this topcoder article.
Note that the value of f is initially 0 because all ai are 0.
Base case: If we have x as a power of 2 to be the input to f, our lemma is trivially true because we have f(x) = BIT(x) and BIT(x) contains the sum of elements from index 1 to x as mentioned in the article linked above. This proves our lemma for values for x with exactly 1 set bit.
Induction Hypothesis: Let's assume that our lemma is true for values of x with at most k bits set where 1 ≤ k. Formally, for values of x with at most k bits set,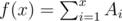
Now, suppose that iteration i of the meta binary search produces the value X, which has exactly k bits set. Now, what happens if we set an additional bit (suppose that it is the bth bit)? We have:
Hence, we now have the fact that given any index x in the actual array, we have the mapping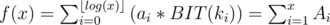
Q.E.D.
With the above lemma, we can use meta binary search to swiftly compute x for which f(x) = V for any given V which is exactly what we were after.
who are you ?
This algorithm is called exponential search.
Here is a Codeforces problem you can practice this technique on: 992E - Nastya and King-Shamans
39424824 is my solution performing this search in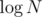
time, vs. 39424729 using plain binary search on the binary indexed tree for a 
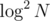search.
can u pls explain how this query function is working in your code?
The same in Petr's blog: https://petr-mitrichev.blogspot.com/2018/02/a-fenwick-bound-week.html
I tried to use this instead of binary search on the interactive problem 1011D - Rocket but my Submission 42010046 gives WA(Unexpected End of file) on Test case 9 even after all the debugging I could possibly do (42010611), I am probably making the most noobish mistake ever but could someone help me out on this?
Is it really useful to do this, when you can do binary search on queries on the fenwick tree?
Apart from the extra $$$log(N)$$$ factor in case of binary search, it doesn't really make any difference right?
So basically, is there some use case where binary lifting would work but binary search won't?
Video explanation of same blog. Link
is there any way that we can use this method in segment trees ??
in fenwick trees the required values can be directly get from bit array as the values are stored in the order that can be used for binary lifting,
but in segment trees we cannot get those values directly, as in segement trees values are stored continuesly not in the order that can be used for binary lifting.
I have implemented the binary lifting with segment trees.
here's the code link for reference : https://hastebin.skyra.pw/upidozejuf.cc
here the method last_ind_with_cur_max, will return the largest index( > start index), such that the maximum from start to that index will be <= cur_max, in o(logn).
doing naively with binary search and segment tree queries will have time complexity of o(logn^2).
Another problem D. Multiset