Introduction
I have no school right now, and there's no tutorials on Tree Isomorphism on Codeforces, so I decided to write one :).
What is a tree isomorphism?
Maybe you recognize the word isomorphic: in the context of abstract algebra when two objects are effectively the same, but are labelled differently. We can extend this to trees as well: two trees are isomorphic if they are the same, but may have different node labels. For example,
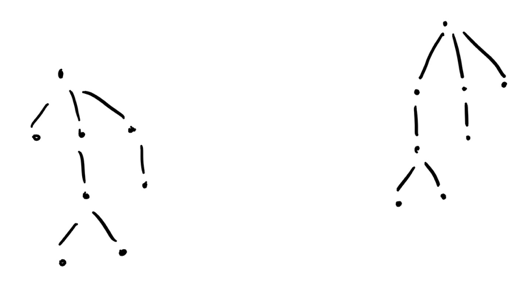 are isomorphic because we can relabel the nodes. If you want a more rigorous definition, then two trees $$$T_1 = (V_1, E_1)$$$ and $$$T_2 = (V_2, E_2)$$$ are isomorphic iff there exists a $$$\phi$$$ for which $$$\phi(E_1) = E_2$$$ and a $$$\phi^{-1}$$$ for which $$$\phi^{-1} (E_2) = E_1$$$.
are isomorphic because we can relabel the nodes. If you want a more rigorous definition, then two trees $$$T_1 = (V_1, E_1)$$$ and $$$T_2 = (V_2, E_2)$$$ are isomorphic iff there exists a $$$\phi$$$ for which $$$\phi(E_1) = E_2$$$ and a $$$\phi^{-1}$$$ for which $$$\phi^{-1} (E_2) = E_1$$$.
What is the problem?
We want to determine if two unrooted trees are isomorphic in $$$\mathcal{O}(N \log N)$$$ time.
If we can solve the problem for rooted trees, can we solve it for unrooted trees?
Yes. We can transform our original problem of checking if two trees are isomorphic into checking if two rooted trees are isomorphic easily. How? We can find the centroids of our first tree and our centroids of our second tree, and then root them at their centroids. So now, we have transformed our unrooted case into a rooted case.
Heuristics
You can skip this, if you'd like. I'm just going to list out some ideas for tree isomorphism checking. All of the following ideas won't solve the problem, but some of them work decently well.
Idea 1: Find the degrees of all nodes and check if $$$\text{oc}_{T1}[i] = \text{oc}_{T2}[i]$$$, where $$$\text{oc}_{T}[i]$$$ is the number of vertices of degree $$$i$$$. If $$$\text{oc}_{T1}[i] = \text{oc}_{T2}[i] \forall i$$$ does not hold, then we know that the trees are not isomorphic.
Idea 2: Root the trees at their centroids. $$$\text{oc}_{T1}[i] = \text{oc}_{T2}[i]$$$, where $$$\text{oc}_{T}[i]$$$ is the number of vertices with subtree size $$$i$$$. If $$$\text{oc}_{T1}[i] = \text{oc}_{T2}[i] \forall i$$$ does not hold, then we know that the trees are not isomorphic.
Idea 3: If the diameters of the tree are not the same, then they cannot be isomorphic.
Idea 4: We know that for fixed $$$k$$$, the number of paths of length $$$k$$$ must be the same in both trees.
If we merge all of the ideas together, we will get a pretty good heuristic and will be able to identify with pretty good accuracy if a tree is isomorphic to another tree. But that's not good enough.
The idea
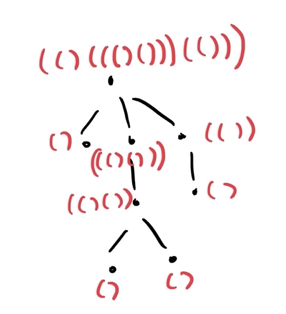
The idea is to parenthesize our tree. We can recursively, say that:
where $$$+$$$ denotes string concatenation. But obviously, the string parenthesization for rooted trees do not always yield the same result, even for isomorphic trees:
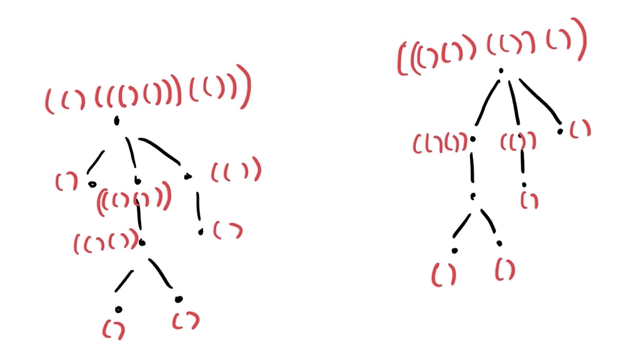
So what can we do? It turns out, we can just "order" the parenthesization. That is, concactenate in increasing or decreasing order of the string parenthesization.
How would it look like if we did that?
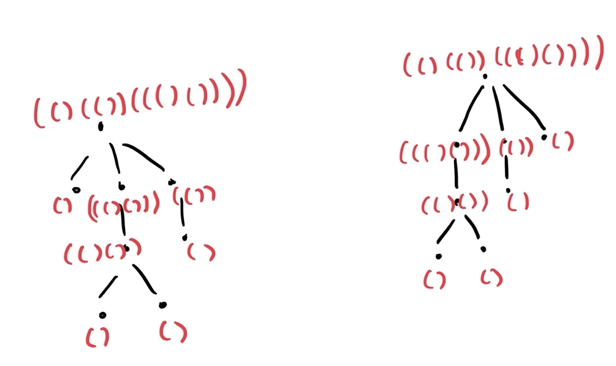
So, in short, the idea is to parenthesize the tree and then concactenate in some fixed order (one easy way is in increasing order of the strings).
But that's $$$\mathcal{O}(N^2)$$$, since we're dealing with a lot of potentially large strings. No problem! We can replace each opening parenthesis with a $$$1$$$ and each closing parenthesis with a 0. For example, $$$(()())$$$ would become $$$110100$$$. We can then convert the binary string to a number, by using it's binary representation. In the case that the number is too large, we can take it modulo some large prime $$$p$$$.
The end.





