| Matrix Exponentiation |
|---|
| Finished |
You are given a graph with $$$n$$$ vertices (numbered $$$1$$$ through $$$n$$$) and $$$m$$$ directed edges. Count paths consisting of $$$k$$$ steps (edges) and print the answer modulo $$$10^9+7$$$. A path can visit the same vertex or edge multiple times.
The first line contains three integers $$$n$$$, $$$m$$$ and $$$k$$$ ($$$1 \leq n \leq 100$$$, $$$0 \leq m \leq n \cdot (n - 1)$$$, $$$1 \leq k \leq 10^9$$$) — the number of vertices, the number of edges and the length of a path.
The following $$$m$$$ lines describe edges. The $$$i$$$-th of these lines contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n, a_i \neq b_i$$$), denoting a directed edge from $$$a_i$$$ to $$$b_i$$$. There are no self-loops or multiple edges.
Print the answer modulo $$$1000000007$$$.
3 4 2 1 2 2 3 3 1 2 1
5
5 10 11 2 3 4 2 2 1 2 4 1 5 5 2 3 2 3 1 3 4 1 2
21305
In the first sample test, we are given the following graph with $$$n = 3$$$ vertices and $$$m = 4$$$ edges.
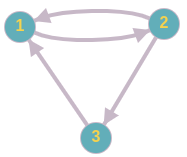
There are 5 paths of length $$$k = 2$$$:
- $$$1 \rightarrow 2 \rightarrow 1$$$
- $$$1 \rightarrow 2 \rightarrow 3$$$
- $$$2 \rightarrow 1 \rightarrow 2$$$
- $$$2 \rightarrow 3 \rightarrow 1$$$
- $$$3 \rightarrow 1 \rightarrow 2$$$
| Name |
|---|




