A forestation is an act of planting a bunch of trees to grow a forest, usually to replace a forest that had been cut down. Strangely enough, graph theorists have another idea on how to make a forest, i.e. by cutting down a tree!
A tree is a graph of N nodes connected by N−1 edges. Let u be a node in a tree U which degree is at least 2 (i.e. directly connected to at least 2 other nodes in U). If we remove u from U, then we will get two or more disconnected (smaller) trees, or also known as forest by graph theorists. In this problem, we are going to investigate a special forestation of a tree done by graph theorists.
Let V(S) be the set of nodes in a tree S and V(T) be the set of nodes in a tree T. Tree S and tree T are identical if there exists a bijection f:V(S)→V(T) such that for all pairs of nodes (si,sj) in V(S), si and sj is connected by an edge in S if and only if node f(si) and f(sj) is connected by an edge in T. Note that f(s)=t implies node s in S corresponds to node t in T.
We call a node u in a tree U as a good cutting point if and only if the removal of u from U causes two or more disconnected trees, and all those disconnected trees are pairwise identical.
Given a tree U, your task is to determine whether there exists a good cutting point in U. If there is such a node, then you should output the maximum number of disconnected trees that can be obtained by removing exactly one good cutting point.
For example, consider the following tree of 13 nodes.
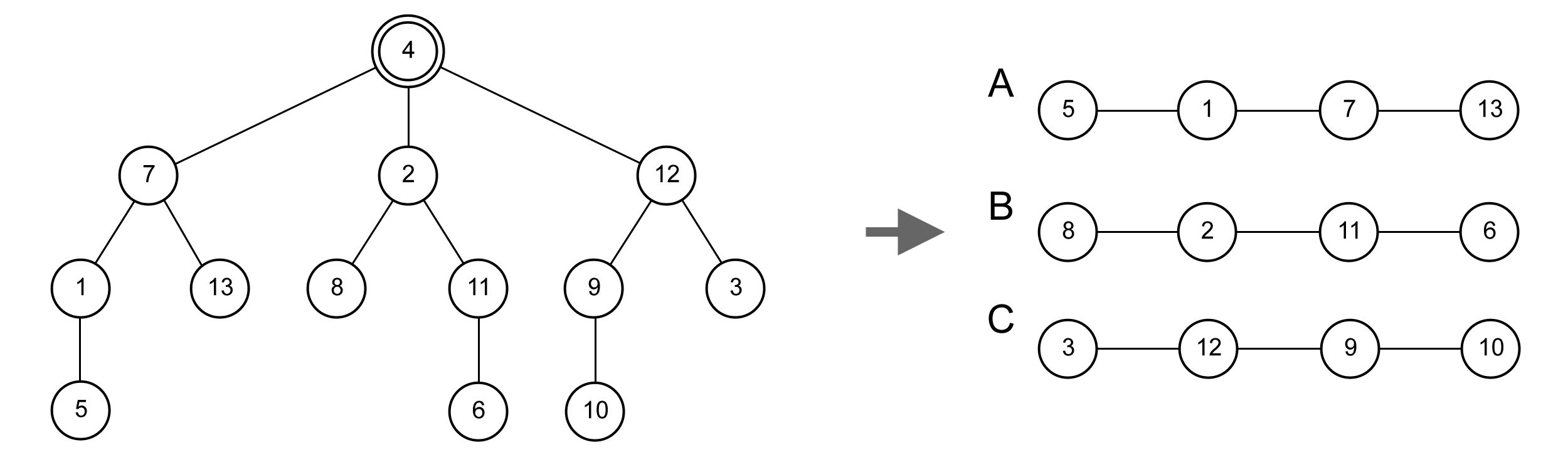
There is exactly one good cutting point in this tree, i.e. node 4. Observe that by removing node 4, we will get three identical trees (in this case, line graphs), i.e. {5,1,7,13}, {8,2,11,6}, and {3,12,9,10}, which are denoted by A, B, and C respectively in the figure.
- The bijection function between A and B: f(5)=8, f(1)=2, f(7)=11, and f(13)=6.
- The bijection function between A and C: f(5)=3, f(1)=12, f(7)=9, and f(13)=10.
- The bijection function between B and C: f(8)=3, f(2)=12, f(11)=9, and f(6)=10.
Input begins with a line containting an integer: N (3≤N≤4000) representing the number of nodes in the given tree. The next N−1 lines each contains two integers: ai bi (1≤ai<bi≤N) representing an edge (ai,bi) in the given tree. It is guaranteed that any two nodes in the given tree are connected to each other by a sequence of edges.
Output in a line an integer representing the maximum number of disconnected trees that can be obtained by removing exactly one good cutting point, or output -1 if there is no such good cutting point.
13 1 5 1 7 2 4 2 8 2 11 3 12 4 7 4 12 6 11 7 13 9 10 9 12
3
6 1 2 1 3 2 4 3 5 3 6
-1
Explanation for the sample input/output #1
This is the example from the problem description.
| Name |
|---|




