| Hello 2022 |
|---|
| Finished |
Circular land is an $$$2n \times 2n$$$ grid. Rows of this grid are numbered by integers from $$$1$$$ to $$$2n$$$ from top to bottom and columns of this grid are numbered by integers from $$$1$$$ to $$$2n$$$ from left to right. The cell $$$(x, y)$$$ is the cell on the intersection of row $$$x$$$ and column $$$y$$$ for $$$1 \leq x \leq 2n$$$ and $$$1 \leq y \leq 2n$$$.
There are $$$n^2$$$ of your friends in the top left corner of the grid. That is, in each cell $$$(x, y)$$$ with $$$1 \leq x, y \leq n$$$ there is exactly one friend. Some of the other cells are covered with snow.
Your friends want to get to the bottom right corner of the grid. For this in each cell $$$(x, y)$$$ with $$$n+1 \leq x, y \leq 2n$$$ there should be exactly one friend. It doesn't matter in what cell each of friends will be.
You have decided to help your friends to get to the bottom right corner of the grid.
For this, you can give instructions of the following types:
- You select a row $$$x$$$. All friends in this row should move to the next cell in this row. That is, friend from the cell $$$(x, y)$$$ with $$$1 \leq y < 2n$$$ will move to the cell $$$(x, y + 1)$$$ and friend from the cell $$$(x, 2n)$$$ will move to the cell $$$(x, 1)$$$.
- You select a row $$$x$$$. All friends in this row should move to the previous cell in this row. That is, friend from the cell $$$(x, y)$$$ with $$$1 < y \leq 2n$$$ will move to the cell $$$(x, y - 1)$$$ and friend from the cell $$$(x, 1)$$$ will move to the cell $$$(x, 2n)$$$.
- You select a column $$$y$$$. All friends in this column should move to the next cell in this column. That is, friend from the cell $$$(x, y)$$$ with $$$1 \leq x < 2n$$$ will move to the cell $$$(x + 1, y)$$$ and friend from the cell $$$(2n, y)$$$ will move to the cell $$$(1, y)$$$.
- You select a column $$$y$$$. All friends in this column should move to the previous cell in this column. That is, friend from the cell $$$(x, y)$$$ with $$$1 < x \leq 2n$$$ will move to the cell $$$(x - 1, y)$$$ and friend from the cell $$$(1, y)$$$ will move to the cell $$$(2n, y)$$$.
Note how friends on the grid border behave in these instructions.
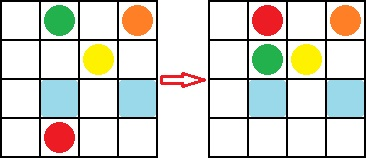 Example of applying the third operation to the second column. Here, colorful circles denote your friends and blue cells are covered with snow.
Example of applying the third operation to the second column. Here, colorful circles denote your friends and blue cells are covered with snow. You can give such instructions any number of times. You can give instructions of different types. If after any instruction one of your friends is in the cell covered with snow he becomes ill.
In order to save your friends you can remove snow from some cells before giving the first instruction:
- You can select the cell $$$(x, y)$$$ that is covered with snow now and remove snow from this cell for $$$c_{x, y}$$$ coins.
You can do this operation any number of times.
You want to spend the minimal number of coins and give some instructions to your friends. After this, all your friends should be in the bottom right corner of the grid and none of them should be ill.
Please, find how many coins you will spend.
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 100$$$) — the number of test cases.
The first line of each test case contains the single integer $$$n$$$ ($$$1 \leq n \leq 250$$$).
Each of the next $$$2n$$$ lines contains $$$2n$$$ integers $$$c_{i, 1}, c_{i, 2}, \ldots, c_{i, 2n}$$$ ($$$0 \leq c_{i, j} \leq 10^9$$$) — costs of removing snow from cells. If $$$c_{i, j} = 0$$$ for some $$$i, j$$$ than there is no snow in cell $$$(i, j)$$$. Otherwise, cell $$$(i, j)$$$ is covered with snow.
It is guaranteed that $$$c_{i, j} = 0$$$ for $$$1 \leq i, j \leq n$$$.
It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$250$$$.
For each test case output one integer — the minimal number of coins you should spend.
410 81 9920 0 0 00 0 0 09 9 2 29 9 9 920 0 4 20 0 2 44 2 4 22 4 2 440 0 0 0 0 0 0 20 0 0 0 0 0 2 00 0 0 0 0 2 0 00 0 0 0 2 0 0 00 0 0 2 2 0 2 20 0 2 0 1 6 2 10 2 0 0 2 4 7 42 0 0 0 2 0 1 6
100 22 14 42
In the first test case you can remove snow from the cells $$$(2, 1)$$$ and $$$(2, 2)$$$ for $$$100$$$ coins. Then you can give instructions
- All friends in the first collum should move to the previous cell. After this, your friend will be in the cell $$$(2, 1)$$$.
- All friends in the second row should move to the next cell. After this, your friend will be in the cell $$$(2, 2)$$$.
In the second test case you can remove all snow from the columns $$$3$$$ and $$$4$$$ for $$$22$$$ coins. Then you can give instructions
- All friends in the first row should move to the next cell.
- All friends in the first row should move to the next cell.
- All friends in the second row should move to the next cell.
- All friends in the second row should move to the next cell.
- All friends in the third column should move to the next cell.
- All friends in the third column should move to the next cell.
- All friends in the fourth column should move to the next cell.
- All friends in the fourth column should move to the next cell.
It can be shown that none of the friends will become ill and that it is impossible to spend less coins.
| Name |
|---|




