Isona is in a train station. This station has two platforms, and between them there are $$$m$$$ parallel railways that can be viewed as infinite straight lines. Each railway is identified with an integer from $$$1$$$ to $$$m$$$, railway $$$1$$$ being the closest to the first platform and railway $$$m$$$ being the farthest. There is a $$$1$$$ meter distance between consecutive railways, as well as between each platform and its closest railway.
Isona is standing on the inner border of the first platform, when she realizes that she forgot to validate her ticket! There is a validating machine on the second platform, exactly opposite her current position (thus, the distance between Isona and the validating machine is $$$m + 1$$$ meters). There are only $$$s$$$ seconds left to validate the ticket and the bridge designated to cross the railways is too far from the validating machine. Therefore, Isona (who is very brave and a little bit careless) will cross the railways running in a straight line perpendicular to the railways themselves. Isona can only run forward (not backward) and she can stay still. When she runs at maximum speed, she needs $$$v$$$ seconds to traverse $$$1$$$ meter. She can run at any speed less than or equal to her maximum speed.
There is only one problem: $$$n$$$ trains are programmed to transit through the railways. The $$$i$$$-th train will use the railway $$$r_i$$$. It will start crossing the straight line between Isona and the validating machine $$$a_i$$$ seconds from now and it will end $$$b_i$$$ seconds from now. Of course, Isona cannot cross a railway when a train is passing. Formally, for every $$$i = 1, \, 2, \, \dots, \, n$$$, Isona is not allowed to be on railway $$$r_i$$$ at any time $$$t$$$ with $$$a_i < t < b_i$$$ (but she is allowed to cross at times $$$a_i$$$ or $$$b_i$$$).
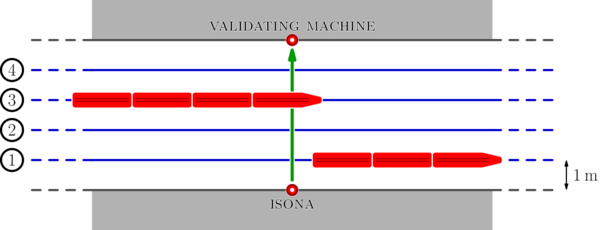
The following picture summarizes the situation. In the picture there are $$$m = 4$$$ railways and two trains are visible; the train going through railway $$$3$$$ is currently crossing the line between Isona and the validating machine.
Isona is a really good runner, but she gets tired every time she has to change her running speed. What is the minimum number of speed changes she has to perform to get to the validating machine on the other platform within $$$s$$$ seconds from now? Note that at the beginning Isona is not running. She can start to run anytime. The instant she starts to run (i.e. her speed becomes positive) is not counted as a speed change.
The first line of the input contains four integers $$$n$$$, $$$m$$$, $$$s$$$, $$$v$$$ ($$$1 \leq n \leq 500$$$, $$$1 \leq m \leq 10$$$, $$$1 \leq s, v \leq 10^9$$$) — the number of trains, the number of railways, the maximum time in seconds Isona can spend crossing the railways, and the number of seconds she needs to traverse $$$1$$$ meter at maximum speed.
Each of the next $$$n$$$ lines contains three integers $$$a_i$$$, $$$b_i$$$, $$$r_i$$$ ($$$1 \leq a_i < b_i \leq 10^9$$$, $$$1 \leq r_i \leq m$$$) — the start and end times of the $$$i$$$-th train crossing the straight line between Isona and the validating machine, and the railway it will be using.
It is guaranteed that, for any two trains $$$i$$$ and $$$j$$$ that go through the same railway (i.e. $$$r_i = r_j$$$), there is at least $$$1$$$ second between them (that is, either $$$a_j \ge b_i + 1$$$ or $$$a_i \ge b_j + 1$$$).
Print the minimum number of speed changes Isona has to perform to get to the validating machine in time. If this is impossible, print $$$-1$$$.
4 3 5 1 1 2 1 3 4 1 2 3 2 3 4 3
0
3 3 12 2 2 10 1 1 6 2 8 12 3
2
8 4 13 2 1 4 1 5 13 1 1 5 2 6 13 2 1 9 3 10 13 3 1 10 4 11 13 4
2
1 1 2 2 1 2 1
-1
In the first sample, if Isona starts running at time $$$t=0$$$ at maximum speed ($$$1$$$ m/s), she will cross each railway just when a train is about to traverse it, and she will arrive at the other platform at time $$$4 = s - 1$$$ without changing speed.
In the second sample, a possible solution with $$$2$$$ speed changes is the following: for the first $$$2$$$ seconds Isona goes at maximum speed ($$$0.5$$$ m/s), then she slows down to $$$0.25$$$ m/s for $$$4$$$ seconds until she reaches the second railway. At that point, she goes at maximum speed again until she reaches the other platform.
In the third sample, Isona can wait $$$2$$$ seconds before starting running. She then runs for $$$5$$$ seconds at maximum speed ($$$0.5$$$ m/s). After that, she waits for $$$1$$$ second not running (or running at $$$0$$$ m/s), and finally she runs again at maximum speed for the last $$$5$$$ seconds. Overall, she changes speed twice.
| Name |
|---|




