This is the easy version of the problem. The only difference between the two versions are the allowed characters in $$$s$$$. In the easy version, $$$s$$$ only contains the character ?. You can make hacks only if both versions of the problem are solved.
You are given a permutation $$$p$$$ of length $$$n$$$. You are also given a string $$$s$$$ of length $$$n$$$, consisting only of the character ?.
For each $$$i$$$ from $$$1$$$ to $$$n$$$:
- Define $$$l_i$$$ as the largest index $$$j < i$$$ such that $$$p_j > p_i$$$. If there is no such index, $$$l_i := i$$$.
- Define $$$r_i$$$ as the smallest index $$$j > i$$$ such that $$$p_j > p_i$$$. If there is no such index, $$$r_i := i$$$.
Initially, you have an undirected graph with $$$n$$$ vertices (numbered from $$$1$$$ to $$$n$$$) and no edges. Then, for each $$$i$$$ from $$$1$$$ to $$$n$$$, add one edge to the graph:
- If $$$s_i =$$$ L, add the edge $$$(i, l_i)$$$ to the graph.
- If $$$s_i =$$$ R, add the edge $$$(i, r_i)$$$ to the graph.
- If $$$s_i =$$$ ?, either add the edge $$$(i, l_i)$$$ or the edge $$$(i, r_i)$$$ to the graph at your choice.
Find the maximum possible diameter$$$^{\text{∗}}$$$ over all connected graphs that you can form. Output $$$-1$$$ if it is not possible to form any connected graphs.
$$$^{\text{∗}}$$$ Let $$$d(s, t)$$$ denote the smallest number of edges on any path between $$$s$$$ and $$$t$$$.
The diameter of the graph is defined as the maximum value of $$$d(s, t)$$$ over all pairs of vertices $$$s$$$ and $$$t$$$.
Each test contains multiple test cases. The first line of input contains a single integer $$$t$$$ ($$$1 \le t \le 2 \cdot 10^4$$$) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 4 \cdot 10^5$$$) — the length of the permutation $$$p$$$.
The second line of each test case contains $$$n$$$ integers $$$p_1,p_2,\ldots, p_n$$$ ($$$1 \le p_i \le n$$$) — the elements of $$$p$$$, which are guaranteed to form a permutation.
The third line of each test case contains a string $$$s$$$ of length $$$n$$$. It is guaranteed that it consists only of the character ?.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$4 \cdot 10^5$$$.
For each test case, output the maximum possible diameter over all connected graphs that you form, or $$$-1$$$ if it is not possible to form any connected graphs.
852 1 4 3 5?????21 2??33 1 2???75 3 1 6 4 2 7???????55 2 1 3 4?????66 2 3 4 5 1??????81 7 5 6 2 8 4 3????????126 10 7 1 8 5 12 2 11 3 4 9????????????
4 1 2 6 4 5 5 8
In the first test case, here are some possible connected graphs that you can form (the labels are indices):
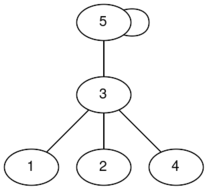 | 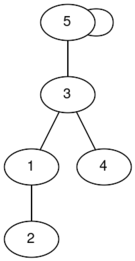 |  |
In the second test case, the only connected graph has a diameter of $$$1$$$.
| Name |
|---|




