| AIM Tech Mini Marathon 1 |
|---|
| Finished |
You have a robot in a two-dimensional labyrinth which consists of N × M cells. Some pairs of cells adjacent by side are separated by a wall or a door. The labyrinth itself is separated from the outside with walls around it. Some labyrinth cells are the exits. In order to leave the labyrinth the robot should reach any exit. There are keys in some cells. Any key can open any door but after the door is opened the key stays in the lock. Thus every key can be used only once. There are no labyrinth cells that contain both a key and an exit. Also there can not be both a wall and a door between the pair of adjacent cells.
Your need to write a program in abc language (see the language description below) that will lead the robot to one of the exits. Lets numerate the labyrinth rows from 0 to N - 1 top to bottom and the columns – from 0 to M - 1 left to right.
In abc language the following primary commands are available:
- move-DIR – move to the adjacent cell in the
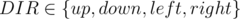 direction. down increases the number of the row by 1, right increases the number of the column by 1. In case there’s a wall or a closed door in this direction, nothing’s happening.
direction. down increases the number of the row by 1, right increases the number of the column by 1. In case there’s a wall or a closed door in this direction, nothing’s happening. - open-DIR – open the door between the current cell and the adjacent one in DIR direction. In case there isn’t any door in this direction or it’s already been opened or the robot doesn’t have a key, nothing’s happening.
- take – take the key in the current cell. In case there isn’t any key or the robot has already picked it up, nothing’s happening. The robot is able to carry any number of keys.
- terminate – terminate the program. This command is not obligatory to use. In case it’s absent the command is added at the end of the program automatically.
Also, there are the following control commands in abc language:
- for-N OPS end – repeat the sequence of the OPS commands N times, 0 < N ≤ 100000. Each loop counter check counts as a command fulfilled by the robot.
- if-ok OPS1 else OPS2 endif – carries out the sequence of the OPS1 commands, if the previous command of moving, taking the key or opening the door was successful, otherwise the sequence of the OPS2 commands is being carried out. Should there be no previous command run, the sequence OPS1 will be carried out. If-ok check counts as a command fulfilled by the robot.
- break – stops the current for loop.
- continue – finishes the current for loop iterations.
Note that the control and the primary commands can be fit into each other arbitrarily.
The robot will fulfill your commands sequentially until it exits the labyrinth, or it runs out of the commands, or the terminate command is run, or the quantity of the fulfilled commands exceeds the bound number 5·106.
In abc language each command is a separate word and should be separated from other commands with at least one space symbol.
You should write a program that prints the sequence of commands leading the robot out of the labyrinth. Of course, as you are a good programmer, you should optimize these sequence.
The number of the non-space symbols in the sequence should not exceed 107. If you succeed in finding the way out of the labyrinth i you’ll be granted the number of points equal to:
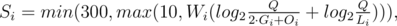
- Wi – labyrinth’s weight, some fixed constant.
- Gi – number of robots moves.
- Oi – number of fulfilled commands. Note that this number includes commands like take executed in the cells with no key, as well as opening commands applied to the already opened doors.
- Li – sequence length in symbols, excluding space symbols and line breaks.
- Q = 10·N·M.
In case your sequence doesn’t lead the robot to the exit you’ll be granted 0 points. Your programs result will be the sum of all Si. You should maximize this total sum.
All labyrinths will be known and available to you. You can download the archive with labyrinths by any of the given links, password to extract files is aimtechiscool:
- https://drive.google.com/file/d/1dkIBfW_Gy6c3FJtXjMXZPMsGKRyn3pzp
- https://www.dropbox.com/s/77jrplnjgmviiwt/aimmaze.zip?dl=0
- https://yadi.sk/d/JNXDLeH63RzaCi
In order to make local testing of your programs more convenient, the program calculating your results (checker) and the labyrinth visualizer will be available. This program is written in python3 programming language, that’s why you’re going to need python3 interpreter, as well as pillow library, which you can install with the following command pip3 install pillow. pip3 is a utility program for python3 package (library) installation. It will be installed automatically with the python3 interpreter.
Example command to run checker and visualizer: python3 aimmaze.py maze.in robot.abc --image maze.png. The checker can be run separately of visualization: python3 aimmaze.py maze.in robot.abc. Flag --output-log will let you see the information of robots each step: python3 aimmaze.py maze.in robot.abc --output-log. Note python3 can be installed as python on your computer.
To adjust image settings, you can edit constants at the beginning of the program aimmaze.py.
The first line contains integers i, W, N, M, x0, y0, C, D, K, E.
- 1 ≤ i ≤ 14 – labyrinth’s number, which is needed for a checking program.
- 1 ≤ W ≤ 1018 – labyrinth’s weight, which is needed for a checking program.
- 2 ≤ N, M ≤ 1000 – labyrinth’s height and width.
- 0 ≤ x0 ≤ N - 1, 0 ≤ y0 ≤ M - 1 – robot’s starting position (x0, y0).
- 0 ≤ C ≤ 2·NM – number of walls.
- 0 ≤ D ≤ 105 – number of doors.
- 0 ≤ K ≤ 105 – number of keys.
- 1 ≤ E ≤ 1000 – number of exits.
The x coordinate corresponds to the row number, y – to the column number. (0, 0) cell is located on the left-up corner, so that down direction increases the x coordinate, while right direction increases the y coordinate.
Each of the next C lines contains 4 integers each x1, y1, x2, y2 – the coordinates of cells with a wall between them in a zero based indexing. It is guaranteed that |x1 - x2| + |y1 - y2| = 1, 0 ≤ x1, x2 ≤ N - 1, 0 ≤ y1, y2 ≤ M - 1. Also there are always walls around the labyrinth’s borders, which are not given in the labyrinths description.
Each of the next D lines contains door description in the same format as walls description. It is guaranteed that doors and walls don’t overlap.
Each of the next K rows contains a pair of integer which are the key coordinates in a zero based indexing.
Each of the next E rows contains a pair of integer which are the exit coordinates in a zero based indexing.
It is guaranteed that the robots starting position as well as keys and exits are located in pairwise different cells.
Print a program in abc language which passes the given labyrinth. Commands have to be separated by at least one space symbol. You can use arbitrary formatting for the program.
1 1 30 30 1 1 1 1 1 1
1 1 1 2
2 2 2 3
1 4
9 0
for-1111
take
open-up
open-left
open-right
open-down
move-left
if-ok
for-11
move-left
take
open-up
open-left
open-right
open-down
end
else
move-right
if-ok
for-11
move-right
take
open-up
open-left
open-right
open-down
end
else endif
endif
move-up
if-ok
for-11
move-up
take
open-up
open-left
open-right
open-down
end
else
move-down
if-ok
for-11
move-down
take
open-up
open-left
open-right
open-down
end
else endif
endif
end
| Name |
|---|




