vfleaking's blog

Codeforces Round #250 Editorial
By vfleaking, 10 years ago, In English

437A - The Child and Homework

We enumerate each choice i, and then enumerate another choice j (j ≠ i), let cnt = 0 at first, if choice j is twice longer than i let cnt = cnt + 1, if choice j is twice shorter than i let cnt = cnt - 1. So i is great if and only if cnt = 3 or cnt =  - 3.

If there is exactly one great choice, output it, otherwise output C.

437B - The Child and Set

We could deal with this by digits.

Because lowbit(x) is taking out the lowest 1 of the number x, we can enumerate the number of the lowest zero.

Then, if we enumerate x as the number of zero, we enumerate a as well, which a × 2x is no more than limit and a is odd. We can find out that lowbit(a × 2x) = 2x.

In this order, we would find out that the lowbit() we are considering is monotonically decresing.

Because for every two number x, y, lowbit(x) is a divisor of lowbit(y) or lowbit(y) is a divisor of lowbit(x).

We can solve it by greedy. When we enumerate x by descending order, we check whether 2x is no more than sum, and check whether there is such a. We minus 2x from sum if x and a exist.

If at last sum is not equal to 0, then it must be an impossible test.

Why? Because if we don't choose a number whose lowbit = 2x, then we shouldn't choose two numbers whose lowbit = 2x - 1. (Otherwise we can replace these two numbers with one number)

If we choose one number whose lowbit = 2x - 1, then we can choose at most one number whose lowbit = 2x - 2, at most one number whose lowbit = 2x - 3 and so on. So the total sum of them is less than 2x and we can't merge them into sum.

If we don't choose one number whose lowbit = 2x - 1, then it's just the same as we don't choose one number whose lowbit = 2x.

So the total time complexity is O(limit).

437C - The Child and Toy

The best way to delete all n nodes is deleting them in decreasing order of their value.

Proof:

Consider each edge (x, y), it will contribute to the total cost vx or vy when it is deleted.

If we delete the vertices in decreasing order, then it will contribute only min(vx, vy), so the total costs is the lowest.

437D - The Child and Zoo

First, there is nothing in the graph. We sort all the areas of the original graph by their animal numbers in decreasing order, and then add them one by one.

When we add area i, we add all the roads (i, j), where j is some area that has been added.

After doing so, we have merged some connected components. If p and q are two areas in different connected components we have merged just then, f(p, q) must equals the vi, because they are not connected until we add node i.

So we use Union-Find Set to do such procedure, and maintain the size of each connected component, then we can calculate the answer easily.

437E - The Child and Polygon

In this problem, you are asked to count the triangulations of a simple polygon.

First we label the vertex of polygon from 0 to n - 1.

Then we let f[i][j] be the number of triangulations from vertex i to vertex j. (Suppose there is no other vertices and there is an edge between i and j)

If the line segment (i, j) cross with the original polygon or is outside the polygon, f[i][j] is just 0. We can check it in O(n) time.

Otherwise, we have 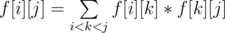, which means we split the polygon into the triangulation from vertex i to vertex k, a triangle (i, k, j) and the triangulation from vertex k to vertex j. We can sum these terms in O(n) time.

Finally,the answer is f[0][n - 1]. It's obvious that we didn't miss some triangulation. And we use a triangle to split the polygon each time, so if the triangle is different then the triangulation must be different, too. So we didn't count some triangulation more than once.

So the total time complexity is O(n3), which is sufficient for this problem.

438D - The Child and Sequence

The important idea of this problem is the property of .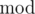

Let .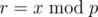

So, .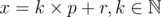

If k = 0, 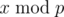remains to be x.

If k ≠ 0, .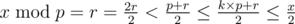

We realize every time a change happening on x, x will be reduced by at least a half.

So let the energy of x become 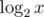. Every time when we modify x, it may take at least 1 energy.

The initial energy of the sequence is .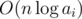

We use a segment tree to support the query to the maximum among an interval. When we need to deal with the operation 2, we modify the maximum of the segment until it is less than x.

Now let's face with the operation 3.

Every time we modify an element on the segment tree, we'll charge a element with 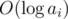power.

So the total time complexity is : .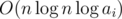

By the way, we can extend the operation 3 to assign all the elements in the interval to the same number in the same time complexity. This is an interesting idea also, but a bit harder. You can think of it.

438E - The Child and Binary Tree

Let f[s] be the number of good vertex-weighted rooted binary trees whose weight exactly equal to s, then we have:

f[0] = 1

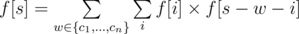
Let F(z) be the generating function of f. That is,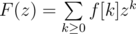

And then let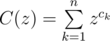

So we have:

F(z) = C(z)F(z)2 + 1

`` + 1'' is for f[0] = 1.

Solve this equation we have:

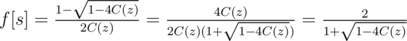
So the remaining question is: how to calculate the multiplication inverse of a power series and the square root of a power series?

There is an interesting algorithm which calculate the inverse of a power series F(z):

We use f(z) ≡ g(z) (mod zn) to denote that the first n terms of f(z) and g(z) are the same.

We can simply calculate a formal power series R1(z) which satisfies R1(z)F(z) ≡ 1 (mod z1)

Next, if we have Rn(z) which satisfies Rn(z)F(z) ≡ 1 (mod zn), we will get:

(Rn(z)F(z) - 1)2 ≡ 0 (mod z2n)

Rn(z)2F(z)2 - 2Rn(z)F(z) + 1 ≡ 0 (mod z2n)

1 ≡ 2Rn(z)F(z) - Rn(z)2F(z)2 (mod z2n)

R2n(z) ≡ 2Rn(z) - Rn(z)2F(z) (mod z2n)

We can simplely use Fast Fourier Transform to deal with multiplication. Note the unusual mod 998244353 (7 × 17 × 223 + 1), thus we can use Number Theoretic Transform.

By doubling n repeatedly, we can get the first n terms of the inverse of F(z) in 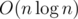time. It's because that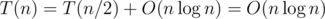

We can just use the idea of this algorithm to calculate the square root of a power series F(z):

We can simply calculate a power series S1(z) which satisfies S1(z)2 ≡ F(z) (mod z2n)

Next, if we have Sn(z) which satisfies Sn(z)2 ≡ F(z) (mod zn), we will get:

(Sn(z)2 - F(z))2 ≡ 0 (mod z2n)

Sn(z)4 - 2Sn(z)2F(z) + F(z)2 ≡ 0 (mod z2n)

Sn(z)2 - 2F(z) + F(z)2Sn(z) - 2 ≡ 0 (mod z2n)

4F(z) ≡ Sn(z)2 + 2F(z) + F(z)2Sn(z) - 2 (mod z2n)

4F(z) ≡ (Sn(z) + F(z)Sn(z) - 1)2 (mod z2n)

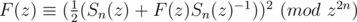
So,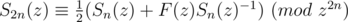

By doubling n repeatedly, we can get the first n terms of the square root of F(z) in 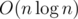time.

That's all. What I want to share with others is this beautiful doubling algorithm.

So the total time complexity of the solution to the original problem is .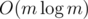

My code

There is an algorithm solving this problem using divide and conquer and Fast Fourier Transform, which runs in 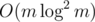. See the C++ code and the Java code for details.

  • Vote: I like it
  • +112
  • Vote: I do not like it

Comments Comments (61)
| Write comment?
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain the solution for 437C — The Child and Toy. In the question it's given that the child can remove one part at a time. Does that mean he can remove one vertex at a time? If yes, then how is it equal to removing the edges as given in the solution of the editorial?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    if you remove a vertex you will break all connections with this vertex, and the cost as given will be sum of costs of all vertices connected to the removed vertex.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      If you remove all the edges connected to a vertex at one time, then answer for the first test case will be 50 not 40. 40 will be the answer when the edges are removed one at a time. But in the question it is given that vertices are to be removed one at a time.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        why is it 50?

        Remove an edge implies removing the vertices connected to it.

        In the first test case

        • remove vertex 3 remove edge u23 with cost v2
        • remove vertex 2 remove edge u12 with cost v1
        • remove vertex 4 remove edge u14 with cost v1
        • remove vertex 1, no more edges

        total v2 + v1 + v1 = 20 + 10 + 10 = 40

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        then you didn't choose the right order of verticesز

        in the first case, you can remove the first vertex, and this will break its connection with the second and the fourth vertex, and the cost will be 60, instead you can remove vertex 4 and 2 and break there connection with vertex 1 and the cost will be 10 + 10 = 20 and since you removed vertex 2 this will also break the connection with vertex 3 and then the total cost will be 50, but this is also not the ideal solution.

        First, remove part 3, cost of the action is 20. Then, remove part 2, cost of the action is 10. Next, remove part 4, cost of the action is 10. At last, remove part 1, cost of the action is 0.

        → Reply
»
10 years ago, # |
  Vote: I like it +20 Vote: I do not like it

The doubling algorithm is truly beautiful! I know that these equations aren't very encouraging, but after understanding the trick I realised 438E is awesome! :P

Thanks for the task (and all the other ones, too)!

→ Reply
»
10 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

Can somebody please explain 437B The Child and Set : why that greedy solution (in a decreasing order) works? I could not understand the editorial due to poor english and presentation (didnt expect this from codeforces tutorials ).

What is 'a' here ? What is this -> Because for every two number x, y, that lowbit(x) | lowbit, 2014 - 06 - 01(y) or lowbit(y) | lowbit, 2014 - 06 - 01(x).

Also, if we don't choose a number whose lowbit = 2^x, then we shouldn't choose two numbers whose lowbit = 2^x - 1 but we can choose four such numbers....so what is he trying to say ?

Please somebody explain in detail...this bit thing always eludes me

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I can't understand the explanation either

    During the contest I thought of creating an array of size limit. Then array[i-1] will store the number 2^k where k is the index of the first 1 bit (from right to left) of number i.

    Then the problem basically asks to find a subset of the values stored in this array, whose total summation is equal to sum. However I couldn't figure out how to solve this part efficiently.

    A simpler explanation of the solution to this problem would be appreciated.

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +6 Vote: I do not like it

    It's similar to the Coin Change problem but with (possibly) many denominations.

    Since the low bit of an odd number is always 1 we have ceil(limit / 2) coins with value 1.

    We know that every number can be obtained as a sum of 1's. Let's denote the number of coins with value 1 as ones.

    1. If sum <= ones then problem solved, use as many 1's as needed.

    2. Else try to decrease sum as much as possible using coins with value greater than 1. If we can make sum <= ones then problem solved (1).

    Unlike the Coin Change problem we don't need to minimize the number of coins, so the best way to decrease sum is to start with the biggest denominations.

    Maybe not the best analogy but it can help :).

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Good idea, I didn't figure this out in the contest. I will try your idea soon. Thx

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That is a very good explanation indeed, rendon. thank you very much.... now understood it very nicely. If u cant make the sum to be zero even after subtracting all the possible lowbit values (which consists of lot of ones) in a decreasing order, that means it is impossible to get the requires sum ... perfect..... :)

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    My fault...I possibly had written some escape character by mistake T_T...

    If there are two numbers whose lowbit = 2x - 1 we chose and we have a number whose lowbit = 2x, then we can replace that two numbers with a single number whose lowbit = 2x, remaining the sum unchanged. So we should choose at most one number whose lowbit = 2x - 1.

    → Reply
»
10 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Can someone please tell me why in "Child and the Zoo" we sort them in increasing way? For me it is the decreasing way that works: when we add new area that has smaller number than areas that it connects then it creates the biggest minimum on the road that has just been created. And that is what we are looking for, isn't it?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    You're absolutely right. It's not easy to make a flawless editorial. :)

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes , I solved it sorting in decreasing way.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It's my fault...sad...Sorry...T_T...

    I have corrected it.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Couldn't understand 437E. What's the final solution? F[0][n-1]? If so, is there a proof that you won't count a triangulation twice when choosing K? I tried to come up with some sort of divide and conquer technique similar to this, but couldn't come up with anything that would prevent the overlapping solutions to be counted twice..

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes, it's just f[0][n - 1].

    Once we choose k, we also choose a triangle. So for different k, the triangulations are different.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Ahh, got it now! At least I was somewhat close to the correct approach, lol.

      Just a minor feedback: when you say "...which means we split the polygon into the triangulation from vertex i to vertex j, a triangle (i, j, k) and the triangulation from vertex j to vertex k."

      Shouldn't it be "...which means we split the polygon into the triangulation from vertex i to vertex k, a triangle (i, j, k) and the triangulation from vertex k to vertex j."?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sorry... It's my fault again. I have corrected it. T_T....

        I need more carefulness when writing the editorial. T_T...

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Still one of the best editorials around here!

          → Reply
»
10 years ago, # |
← Rev. 5   Vote: I like it 0 Vote: I do not like it

why is the date displayed randomly in some portion of the editorial of 437B - The Child and Set

the line that contains "Because for every two number x, $y$, that ..."

Something must be wrong with the MathJax rendering

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can somebody please elaborate 437C — The Child and Toy. Please.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    This was my reasoning to solve this problem:

    For each edge e connecting nodes u and v, the cost to remove e can be f(u) if removed with node u or f(v) if removed with node v. Since we want to minimize the total cost we should remove e with the minimum cost. How?

    Indeed my idea was not to disconnect the graph but to construct it, we start with an empty graph, then add the nodes one by one in ascending order of f(node), the new node should be connected only with the existing nodes.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem B is a nice problem, the algo is amazing~

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

My straightforward solution 6770869 for problem 437E - The Child and Polygon with an intended complexity O(N3) got TLE. After a bit optimization (just by a constant factor) it has passed 6774608. I am a bit disappointed, why there was such a tight time limit? In a competition like this (where we don't get a full feedback) authors usually let even unoptimized solution with the correct complexity pass. Why this wasn't the case? Have any of you experienced a similar problem?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +16 Vote: I do not like it

    Even with this tight TL my O(N^4) solution passed with triple gap:) 6769384

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Thank you for your response. The mistake probably wasn't in the time limit, but in my memoization ;-) I expected that the number of ways is always nonzero and used that value as "not calculated yet". But it can be zero for a collinear points subproblem. It makes me feel much better about the problem!

      → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I have: 5430175, when my deque<> experienced too many reallocations due to being declared in a loop. Solutions with worse complexity and better constant factor passed, my optimal solution didn't.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For the first problem 437A Can someone explain why the answer for testcase 30 A.h B.asdf C.asqw D.qwertasdfg

is C instead of D? I assumed that since D is twice longer than all other options?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Both A and D are the great choices. So the child choose C.

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    in this test case, you have two possible choices, A and D

    because D is twice longer than all, and A is twice smaller than all

    and the problem statement says:

    If there is exactly one great choice then the child chooses it. Otherwise the child chooses C (the child think it is the luckiest choice).

    so the answer is C

    i hacked 9 contestants with a case Like this one :D

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Does anyone know a fast way to calculate the square root of a number by prime (or not prime) modulo?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Cipolla's algorithm is waiting for you.

    → Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Hi may someone explain 438D - The Child and Sequence better?, thanks.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Need help with div 2 B The Child and Set

This is the approach I took to solve it:

Iterate over all numbers from 1 to limit and decrease lowbit of each number from the sum (if it is not possible, then just continue to next number)

But, for some reason, the order in which I consider the numbers matters. If I try all numbers from 1 to limit, I get wrong answer (6785689). But, if I try numbers in the reverse order i.e. from limit down to 1, I get Accepted (6785709).

Can anyone explain why this happened?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think it is because that when you try numbers from limit down to 1, you'll have many numbers whose lowbit = 1 to make the sum equal to the sum this problem required.

    Just like there is a bottle, if you put big stones first and then put small stones will possibly fill the bottle. But if you put small stones first and then put big stones will possibly remain much empty room in the bottle.

    I don't know your later algorithm is right or wrong. Maybe my data is too weak......? >_<...

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I am not completely convinced about my algorithm, too. I don't know if it can be proved.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Your algorithm is surprisingly correct, with a rather convoluted proof. I'm not sure about the details, but basically you prove that your algorithm is correct for small values of limit, then you can also prove that for large values of limit, the sum will diminish quickly enough to reduce to a proven result or otherwise is too large that even with the algorithm in the editorial it's impossible. Probably the thing that saves you is that the small cases are indeed true: lowbit(1) = 1, lowbit(2) = 2, so you can prove for limit ≤ 2 and sum ≤ 3 either your algorithm solves it or your algorithm correctly states it's impossible.

        I'm still looking for a better proof. Let's see...

        → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Should I call the process of analyzing the complexity in 438D potential analysis?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone elaborate on how to solve 437D - The Child and Zoo? I don't understand the editorial.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    Begin by sorting all the vertices (areas) according to the number of animals in it, in decreasing order. Also begin with an empty graph.

    Now add the vertices one by one into the graph in our new order, along with the edges (roads) connected to it.

    Whenever we add a vertex v, we introduce a new component in the graph, namely that single vertex. Whenever we add an edge vi for some existing vertex i to the graph, we might join two components, the component containing v (denote A) and the component containing i (denote B). If this is the case, then any path from A to B must necessarily passes edge vi, and therefore passes the vertex v. Due to our sorting of the vertices, v must have the least cost among all vertices present, and so the value of f of this path is av, the number of animals in v.

    For example, take the first test case:

    4 3
10 20 30 40
1 3
2 3
4 3

    Sorting the vertices, we have the order 40, 30, 20, 10. So first we introduce the fourth vertex. Clearly there's no edge added here, as the graph only contains one vertex.

    Next, we introduce the third vertex. Now we have vertices 4 and 3, and we also have the edge 4 - 3. We add the edge 4 - 3 to the graph, which apparently joins two components together. Denote the component with 3 as A, and the component with 4 as B. (Note that A only contains the vertex 3, and B only contains the vertex 4.) Thus any path connecting A and B must visit vertex 3, and hence has a minimum animal of a3 = 30. There is |A||B| = 1·1 = 1 such path, namely 3 - 4. This gives f(3, 4) = 30.

    Introduce the second vertex and the edge 2 - 3. Now, again, the component with 2 is now connected to the component with 3 (namely 3 and 4). Denote again A, B accordingly. Any path joining A and B must visit vertex 2 and has minimum animal of a2 = 20. There are |A||B| = 1·2 = 2 such paths, namely 2 - 3 and 2 - 4. So f(2, 3) = f(2, 4) = 20.

    The same can be said for vertex 1, giving f(1, 2) = f(1, 3) = f(1, 4) = 10, hence the result.

    In the second test case, there will be a road that connects two vertices in the same component (if you process the edges from top to bottom, this is edge 3 - 1). We ignore such edges.

    In the third test case, when you introduce vertex 5, you will connect it with two components, component 1, 2, 4 and component 6, 7. This is why I keep saying A to be the component containing the current vertex as opposed to only the current vertex alone; after you process edge 4 - 5, you will now have the component 1, 2, 4, 5, thus when you process edge 5 - 6, you will connect |A||B| = 4·2 = 8 such paths connecting 1, 2, 4, 5 to 6, 7.

    I hope this is clearer, but just ask if you still don't understand.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you, I understand the solution now. It seems a bit harder than the typical Div2D/Div1B problem though.

      → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      very well explained!

      → Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Could someone please tell me why the equation F(z) = C(z)F(z)2 + 1 in 438E has only one solution?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    starts with either 1 or  - 1. If you use the latter root, for some power series P; and inverse doesn't exist.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I am sorry that I still don't understand. Could you please give a more detailed explanation? Thank you!

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        Let's consider power series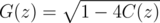

        Let's assume G(z) = b0 + b1 * z + b2 * z2 + b3 * z3 + ...

        It's easy to find that b0 is either 1 or -1.

        If b0 is -1.then 1 + G(z) = b1 * z + b2 * z2 + b3 * z3 + ... = z(b1 + b2 * z + b3 * z2 + ...)

        So we can find a power series P(z),for which zP(z) = G(z)

        It's easy to find that we can never find a Q(z), for whick zP(z)Q(z) = 1

        i.e.when b0 =  - 1 the inverse of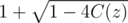 doesn't exist

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        For example, if C(z) = 2z - 4z2 then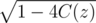 is either 1 - 4z or  - 1 + 4z. If we choose  - 1 + 4z then 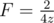, which doesn't exist. If we choose 1 - 4z then .

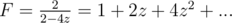        Also, quadratic equations usually have two solutions.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Thanks to the explanations, I have understood this algorithm. Actually there can be two different square roots but only one of them could keep the inverse exist. By the way, I do not know clearly the defination of the notation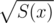 for a formal power series S(x), but I guess it should be unique. Can someone please answer this question? How is it defined?

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          It's defined as follow:

          Let .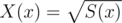

          Then X(x)2 = S(x).

          Modulo xn, it becomes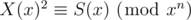

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            But there can be two different X(x)s which satisfy X(x)2 = S(x). So which one does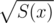 refer to? In the editorial above 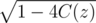refers to the one starting with 1, so does it mean that 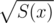should always contain a non-negative constant?

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              10 years ago, # ^ |
              ← Rev. 6   Vote: I like it +5 Vote: I do not like it

              In this problem, it's .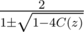

              So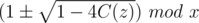 must be non-negative.

              Due to this, we must take  - .

              Let all the coefficient be negative, then you can get another root which satisfy the equation X(x)2 = S(x)

              → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For Div2B (The Child and the Set), I came up with a different solution which runs pretty efficiently. The idea is to continuously "split" numbers that have either already been used or are larger than the limit. We take all the 1 bits in sum and make them numbers (so a sum of 100101 would become 100000, 100, and 1), and split the numbers that don't satisfy the limit.

When splitting a number whose lowbit is x, we create two new numbers with lowbit (x — 1). So by splitting 100, we create numbers 10 and 110 or 1010 or 1110, etc, such that by using any two of these numbers with lowbit (x — 1) we can sum to a number of lowbit (x). Take two of these two numbers and split them again if necessary (above limit or already used). If the number isn't used and is below the limit, we mark it as used, and move on to split the next number.

The case where we can't split anymore (lowbit = 1, numbers like 111, 11, or 1) ends up becoming the case where we can't reach the sum. If we run out of numbers to split, then that means we have finished the problem, because all numbers satisfy the limit and are unique.

Code: 6792767

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    would you like to tell me the complexity of your solution..?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I believe it's O(limit) because we split each number under the limit at most once, though it varies a lot depending on the bits in the sum.

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone please explain the solution to 438D : Child and Sequence. I cannot understand it fully. I do understand that there cannot be more than log2x changes on x. But I don't get the things after that.

Thanks ! :D

→ Reply