466A - Выгодный проезд
Решение этой задачи основано на двух утверждениях:
— Если m·a ≤ b, то вообще не имеет смысла покупать абонементы.
— Иногда имеет смысл купить абонементов на суммарное количество проездов больше чем нужно.
Если нам выгодно купить абонемент на проезд, то максимальное количество абонементов которое мы используем полностью будет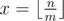 
. Для оставшихся n - m·x проездов мы можем либо накупить билетов, либо купить еще один абонемент и использовать его не полностью.
Асимптотика: O(1)
Решение: 7784793
466B - Чудо-комната
Без ограничения общности можем считать, что a ≤ b.
Во первых, надо рассмотреть случай, в котором уже можно поселить всех людей. Если 6·n ≤ a·b, то ответ a·b a b.
В ином случае нам нужно увеличить какую-то сторону(возможно обе). Делать это будем так: переберем меньшую сторону комнаты newa (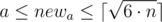
), после того, как мы зафиксировали newa, другую сторону можно посчитать как 
.
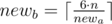По всем таким newa и newb, если b ≤ newb, выбираем такие, произведение которых наименьшее.
Понятно, что рассматривать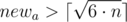 
не имеет смысла, так как мы можем просто ее уменьшить и получить комнату меньшей площади. При этом она будет удовлетворять условию, так как 
.
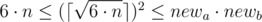Также нужно внимательно следить за тем, чтобы значения не вылезли за используемый тип данных.
Бонус: можете ли вы уменьшить верхнюю оценку перебора меньшей стороны?
Асимптотика: 
Решение: 7784788
466C - Количество способов
Нужно заметить тот факт, что если сумма всех элементов массива равна S, то сумма чисел в каждой части, на которые мы разобьем массив, будет равна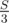 
.
Таким образом, если S не делиться на 3 — то ответ 0.
Иначе, давайте переберем конец первого блока i (1 ≤ i ≤ n - 2) и если сумма чисел от первого до i-го равна 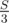, то значит нам к ответу надо прибавить количество таких j (i + 1 < j), что сумма чисел от j-го до n-го тоже равна .
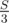Создадим массив cnt[], где в i-й позиции будем хранить 1, если сумма элементов массива от i-го до n-го равна 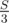, и 0 в других случаях. Теперь, чтобы посчитать ответ, нам нужно уметь быстро считать сумму cnt[j] + cnt[j+1] + ... + cnt[n]. Делать это можно разными структурами данных, но наиболее легким вариантом есть такой: построим массив частичных сумм sums[] на массиве cnt[], где в j-м элементе будет храниться сумма cnt[j] + cnt[j+1] + ... + cnt[n]. Считать его очень просто: sums[n] = cnt[n], sums[i] = sums[i+1] + cnt[i] (i < n).
Таким образом получаем очень простое решение: для каждого i если сумма чисел от первого до i-го равна 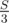, прибавить к ответу sums[i+2].
Асимптотика: O(n)
Решение: 7784781
466D - Увеличьте последовательность
Задачу предполагалось решать динамическим программированием. Пусть dp[i][opened] — количество способов покрыть отрезками префикс массива 1..i так что после i-того элемента массива еще открыто opened отрезков.
Рассмотрим возможные варианты открытия/закрытия отрезков в какой-то позиции массива:
- ] закрываем открытый ранее
- [ открываем новый
- [] добавляем отрезок длины 1)
- ][ закрываем уже открытый и открываем новый
- - ничего не открываем и не закрываем
Теперь поймем как строить переходы такой динамики. Сперва поймем что в текущий момент a[i] + opened может быть равен либо h, либо h - 1. Иначе искомое количество способов — 0.
Рассмотрим отдельно эти два случая:
1) a[i] + opened = h
Это означает что количество открытых отрезков после i-го максимально возможное. Таким образом, возможные варианты состояния некоторых отрезков в i-ой позиции следующие:
- [ Открываем новый отрезок. Возможно только если opened > 0. dp[i][opened] += dp[i-1][opened + 1]
- - dp[i][opened] += dp[i-1][opened]
Остальные варианты невозможны поскольку иначе итоговое значения a[i] будет больше h(когда отрезок заканчивается в текущей позиции он увеличивает значение в ней, но не считается в opened, по определению динамики.
2) a[i] + opened + 1 = h
Тут рассматриваются способы когда i-ый элемент был увеличен на opened + 1, но после i-го остаются открытыми лишь opened. Таким образом получаем следующие возможные варианты:
- ] — закрываем один из уже открытых отрезков(это можно сделать opened + 1 cпособами, поскольку после i-го осталось открытыми лишь opened). dp[i][opened] += dp[i-1][opened + 1] * (opened + 1)
- [] — создаем отрезок длины 1. dp[i][opened] += dp[i-1][opened]
- ][ — Возможно только если opened > 0. Количество способов выбрать отрезок который мы закроем будет равна opened. dp[i][opened] += dp[i-1][opened] * opened
Начальные значения — dp[1][0] = (a[1] == h || a[1] + 1 == h?1:0); dp[1][1] = (a[1] + 1 == h?1:0)
Ответ — dp[n][0].
Асимптотика: O(n)
Решение: 7784697
466E - Граф информаций
Представим всю структуру компании в виде ориентированного графа(если у — начальник х, то в графе будет ребро y -> x). Не сложно заметить, что после каждой выполненной операции наш граф будет лесом. По сути третий запрос — проверить лежит ли сотрудник, которому дали пакет номер i в поддереве вершины x в графе построенном после обработки всех запросов до текущего. Граф, полученный после обработки всех запросов на назначения начальника — назовем финальным. Так же, будем говорить что 2 вершины находятся в одной компоненте связности, если они лежат в одной компоненте в графе полученном из нашего заменой ориентированных ребер на неориентированные.
Рассмотрим следующее утверждение: вершина у является предком вершины х в текущем графе (после обработки первых i запросов) тогда и только тогда, когда у и х находятся в одной компоненте связности, и в финальном графе у является предком х.
Доказательство: Если в какой-то момент вершина у является предком х, то очевидно они лежат в одной компоненте связности а также, вследствии того, что граф всегда будет лесом и ребра не удаляются, и в финальном графе у останется предком.
Наоборот же, доказательство почти аналогично. Из того что у является предком х в финальном графе, следует что между этими вершинами существует ровно один путь. Из предположения, что в какой-то промежуточный момент эти 2 вершины принадлежат одной и той же компоненте связности, следует что ни одно из ребер на пути из у в х не было удалено. Окончательно получаем, что в этот момент времени, удовлетворяющий условию, x лежит в поддереве вершины у. Что и требовалось доказать.
Будем решать задачу оффлайн. После каждого запроса на добавления пакета информации будем сразу отвечать на все запросы касательно этого пакета. Помимо этого воспользуемся системой непересекающихся множеств для определению в одной/разных ли компонентах связности лежат вершины. Отвечать на запрос при этом становится очень просто: проверка на принадлежность вершин одной компоненте, а так же проверка того, что у — предок х в финальном дереве(которое построим сразу, выполнив все запросы первого типа). Определять последнее можно за O(1) с помощью массивов времен входа/выхода построенным обходом в глубину(v — предок u <=> (in[v] ≤ in[u] and out[u] ≤ out[v]). Запрос же первого типа — просто необходимость объединить два дерева в СНМ.
Бонус: Придумайте, как решать задачу онлайн?
Асимптотика: O(n * u(n)), где u — обратная функция Аккермана.
Решение: 7784662
