Problem A – Academia

ENGLISH

This is a Dynamic programming (and/or simulation) question. It's a derivative from the classic Knapsack Problem.

First we do vector, with size from 0 to T_max (T_max + 1), where we can simulate "how heavy is our bag", that is, how much time we spend.

Initially the vector is filled with zeros, because we have no Power of Muscle.

For every exercise we will do the following:

1) We are going to see the vector between [0, T_max - T_exercise], this is our storage vector for every exercise.

2) For t_i in [0, T_max - T_exercise] we will propagate the sum of Power of Muscle from vector[t_i] and P_exercise to the next time.

3) Doing:

vector[t_i + T_exercise] = max(vector[t_i] + P_exercise, vector[t_i + T_exercise])

OBS: Do ti in [0, T_max - T_exercise] goes from right to left to not have a overlapping of Power of Muscle.

At the end, search for the higher value of P in the vector and print.

Time: O(T_max * n).

PORTUGUESE

Esta é uma questão de programação dinâmica e/ou simulação. Ela é uma derivada do clássico Problema da Mochila.

Primeiro faremos um vetor, de tamanho de 0 até T_max (T_max + 1), onde simularemos o "quão pesada está nossa mochila", ou seja, o quanto tempo gastamos.

Inicialmente o vetor estará preenchido com zeros, pois não teremos nenhum Poder de Musculação.

Para cada exercício faremos as seguintes ações:

1) Iremos ver o vetor entre [0, T_max - T_exercício], esse vetor é nosso armazenamento para cada teste.

2) Para t_i entre [0, T_max - T_exercício] iremos propagar a soma do Poder de Musculação do vetor[t_i] e o P_exercício para o próximo tempo.

3) Faremos então:

vetor[t_i + T_exercício] = maior(vetor[t_i] + P_exercício, vetor[t_i + T_exercício])

OBS: Fazer ti entre [0, T_max - T_exercício] ir da direita para esquerda para não haver sobreposição de Poder de Musculação

No final procurar o maior valor de P no vetor e imprimir.

Tempo: O(T_max * n).

Problem B – Bento

ENGLISH

It is a brute force question. It is not given the size of the rectangular room, so it can be any value. The principle question is you analyze if is possible to make something rectangular with a number N of tiles, independently of the room size.

Than the number of tiles will be the number of tiles in colummn multiplied by the number of tiles in row.

For example, 8 tiles -> you can use 2 for column and 4 for row, and vice-versa, being: 2 * 4 = 8.

So we want to know if L * C = N, but L and C cant be 1, so N have to be multiple of L and C.

For that, if N is prime than it cant done, otherwise it can be done.

Since the maximum size of N is 10¹² it is needed to make a faster method to analyze divisors of N, verifying from 1 to 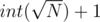, if some of it in this interval divide N, than it is not prime, otherwise it is prime.

The worst case of N is 10¹², than we do up to 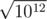maximum, that is equals to 10⁶.

Another observation, 10¹² overflows the size of integer in C/C++/JAVA, for that we use 'unsigned long long int' for C/C++ or 'BigInteger' for Java. Outra observação, 10¹² estoura o tamanho de inteiro em C/C++/JAVA, por isso em C/C++ use 'unsigned long long int' ou 'BigInteger' no Java.

Time:

PORTUGUESE

É uma questão de força bruta. Não é dado o tamanho da sala retangular, então pode ser de qualquer valor. O princípio da questão é você analisar se, independentemente do tamanho da sala, é possível fazer algo retangular com o número N de azulejos.

Então o número de azulejos vai ser o número de azulejos "em coluna" vezes o número de azulejos "em linha".

Por exemplo, 8 azulejos -> você pode usar 2 pra coluna e 4 pra linha, e vice-versa, ficando: 2 * 4 = 8.

Então queremos saber se L * C = N, porém L e C não podem ser 1, logo N tem que ser Múltiplo de L e C.

Para isso, se N é primo então não dá pra fazer, se N não é primo então dá pra fazer.

Como o tamanho máximo de N é 10¹² é preciso fazer o método rápido para analisar os divisores de N, verificando de 1 até 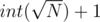, se algum desses neste intervalo divide N, então não é primo, caso contrário é primo.

Então para o pior caso de N ser 10¹², faremos até 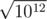que é igual a 10⁶.

Outra observação, 10¹² estoura o tamanho de inteiro em C/C++/JAVA, por isso em C/C++ use unsigned long long int ou BigInteger no Java.

Tempo:

Problem C – Codex

ENGLISH

This is a question os implementation with two viable solutions, one with Binary Search and another with Mp/Hash. We will explain the most easy way.

We will create two Maps (One for given a index return the element and the other for given a element return the index).

Map M, M[index] = element
Map V, V[element] = index

We will manipulate both.

For the operation 1:

index = V[element]
next = M[(index+1) MOD n]
indexnext = V[next]
V[element] = indexnext
V[next] = index
M[index] = next
M[indexnext] = element

From that we have switchs in time O(logn).

For the operation  - 1 it will be similar, but using the previous, remember the case the element is the smaller and swaps with the higher.

For print the result we will do a loop i from 0 to n - 1 print M[i].

PORTUGUESE

É uma questão com duas soluções viáveis uma com implementação com técnica de programação (Busca Binária) ou implementação com Map/Hash. Explicaremos a forma mais fácil.

Criaremos dois Maps (Um para dado o índice ter o elemento e outro para dado o elemento ter o índice):

Map M, M[índice] = elemento
Map V, V[elemento] = índice

Iremos manipular os dois.

Para operação 1:

índice = V[elemento]
próximo = M[(índice+1) MOD n]
índicepróximo = V[próximo]
V[elemento] = índicepróximo
V[próximo] = índice
M[índice] = próximo
M[índicepróximo] = elemento

A partir daí teremos trocas em tempo O(logn).

Para a operação teremos  - 1 será análogo, porém para o anterior, lembrando do caso do elemento ser o menor e trocar com o maior.

Para imprimir o resultamos, faremos um laço de i indo de 0 até n - 1 imprimindo M[i].

Problem D – Dijkstra

ENGLISH

This is a Graph question using the knowledge of LCA (Lowest Common Ancestor). Whatever naive solution is accepted, it just have to look like a LCA algorithm. First we will root the graph from any vertex.

For the example of case 2, lets root the node 1. To root the Tree, we can use BFS or DFS algorithm, where we storage the father and the level of the vertex i. The father of 1 is  - 1 and the level of 1 is 0, by default.

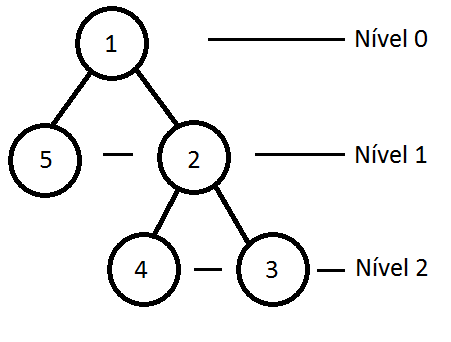
Now to know who is the lowest common ancestor we have to following algorithm.

We have u and v vertex. Lets define u as the vertex with higher level, and v the vertex with lower level.

Lets up u on the tree to make him the same level as v.

while level[v] != level[u] do
    u = father[u]

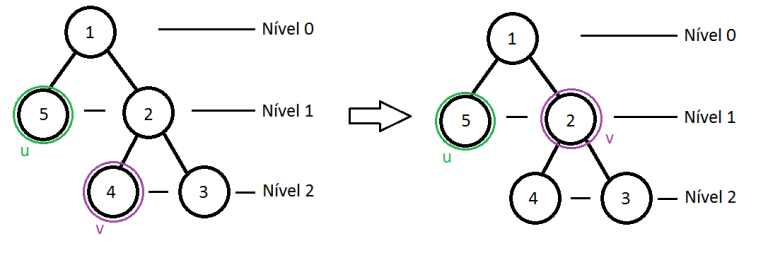
After that, we will up simultaneously both v and u to find the commom vertex and return him.

while u != v do
    u = father[u]
    v = father[v]
return u

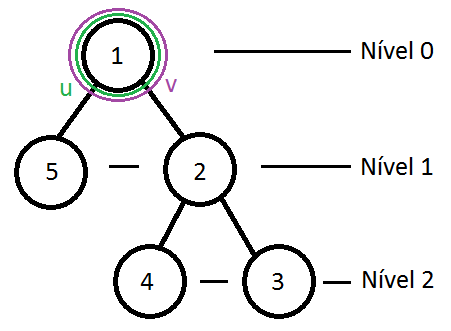
Time: O(n), worst case, it is a linked list.

PORTUGUESE

É uma questão de Grafo utilizando o conhecimento de LCA (Lowest Common Ancestor — Menor Ancestral Comum). Qualquer solução ingênua é aceita desde que tenha a lógica de um LCA. Primeiro iremos enraizar o grafo a partir de um vértice qualquer.

Exemplo do caso 2, vamos enraizar em 1. Para enraizar podemos usar o algoritmo de Busca em Profundidade ou Largura, onde armazenaremos o pai e o nível do vértice i. Para o pai de 1 é  - 1 e o nível de 1 é 0, por padrão.

Agora para saber quem é o menor ancestral comum temos seguinte algoritmo.

Temos u e v que é o número do vértice. Vamos fazer com que o u seja o vértice de maior nível, e v é o vértice de menor nível.

Vamos subir o u para ficar no mesmo nível de v.

Enquanto nível[v] != nível[u] faça
    u = pai[u]

Após isso, você vai subir simultaneamente v e u até achar um vértice que seja comum e retornará ele.

Enquanto u != v faça
    u = pai[u]
    v = pai[v]
retorne u

Tempo: O(n), pior caso, seja uma lista encadeada.

Problem E – Finding Paths

ENGLISH

This is a Graph question with a simple Breadth-First Search Algorithm$(BFS)$ aplication.

The first ideia is to propagate the lower value using the BFS at (0, 0).

Create 3 vectors.

Vector G, where we storage the graph in matrix form. Vector Visited, binary vector where 1 is visited and 0 is not visited. Vector Answer, vector where we will propagate the lower value to (N - 1, N - 1) position.

Starting at (0, 0), propagate for all possible ways (Up, Down, Left, Right), that is, (0, 1) and (1, 0) in this case.

For every Vertex that we will analyse in the BFS:

If j < n-1 and Visited[i][j+1] == 0 and G[i][j+1] != '#' then
    Answer[i][j+1] = min(Answer[i][j] + int(G[i][j+1]), Answer[i][j+1])
    Add to Queue((i,j+1))
If i < n-1 and Visited[i+1][j] == 0 and G[i+1][j] != '#' then
    Answer[i+1][j] = min(Answer[i][j] + int(G[i+1][j]), Answer[i+1][j]) 
    Add to Queue((i+1,j))
If i > 0 and Visited[i-1][j] == 0 and G[i-1][j] != '#' then
    Answer[i-1][j] = min(Answer[i][j] + int(G[i-1][j]), Answer[i-1][j]) 
    Add to Queue((i-1,j))
If j > 0 and Visited[i][j-1] == 0 and G[i][j-1] != '#' then
    Answer[i][j-1] = min(Answer[i][j] + int(G[i][j-1]), Answer[i][j-1])
    Add to Queue((i,j-1))

At the end, compare the result: Answer[N - 1][N - 1] with the life.

Time: O(n²), where the worst case is to visit all the positions at the matrix NxN.

PORTUGUESE

É uma questão de Grafo com uma simples aplicação do algoritmo de Busca em Largura (BFS).

Primeira ideia é propagar o menor valor usando o BFS no (0, 0).

Criaremos 3 vetores.

Vetor G, que é onde carregaremos o Grafo em forma de matriz. Vetor Visitados, vetor binário onde 1 é visitado e 0 é não visitado. Vetor Resposta, vetor onde iremos levar o menor valor até a posição (N - 1, N - 1).

Iniciando em (0, 0), propagamos para todos os possíveis (Cima, Baixo, Esquerda, Direita), ou seja, (0, 1) e (1, 0).

Para cada Vértice que vamos Analisar no BFS:

Se j < n-1 e Visitados[i][j+1] == 0 e G[i][j+1] != '#' então
    Resposta[i][j+1] = menor(Resposta[i][j] + inteiro(G[i][j+1]), Resposta[i][j+1])
    Adicionar a Fila((i,j+1))
Se i < n-1 e Visitados[i+1][j] == 0 e G[i+1][j] != '#' então
    Resposta[i+1][j] = menor(Resposta[i][j] + inteiro(G[i+1][j]), Resposta[i+1][j]) 
    Adicionar a Fila((i+1,j))
Se i > 0 e Visitados[i-1][j] == 0 e G[i-1][j] != '#' então
    Resposta[i-1][j] = menor(Resposta[i][j] + inteiro(G[i-1][j]), Resposta[i-1][j]) 
    Adicionar a Fila((i-1,j))
Se j > 0 e Visitados[i][j-1] == 0 e G[i][j-1] != '#' então
    Resposta[i][j-1] = menor(Resposta[i][j] + inteiro(G[i][j-1]), Resposta[i][j-1])
    Adicionar a Fila((i,j-1))

No final comparar o resultado: Resposta[N - 1][N - 1] com a vida.

Tempo: O(n²), que é o pior caso de ter que visitar todos os pontos da matriz NxN.

Problem F – Making life easier for Miguel

ENGLISH

It is a brute force question, with binary search if you like.

The binary number formed by 1's is a decimal number in the form 2^k - 1.

For that we need to find a k that satisfy that condition, where 10¹⁸ ≤ 2⁶⁰, then we need just to make 60 iteracions to analyze.

The easyest and fastest method is to use a bit-to-bit operation. Doing the following: N&(N + 1), for example:

Than, if N&(N + 1) is equals to 0, than N is in 2^k–1 form, otherwise no.

Time: Bit-to-Bit "O(1)", Analyze O(logk).

PORTUGUESE

É uma questão de força bruta, com otimização em busca binária se quiser.

O número em binário onde é formado só por 1's é um número decimal da forma 2^k - 1.

Para isso só precisamos achar um k que satisfaça essa condição, onde 10¹⁸ ≤ 2⁶⁰, então precisaremos fazer 60 iterações de análise.

O método mais fácil e rápido é utilizar operação bit-a-bit. Fazemos o seguinte: N&(N + 1), por exemplo:

Então, se N&(N + 1) é igual a 0, então N é da forma 2^k–1, caso contrário não.

Tempo: Bit-a-Bit "O(1)", Analise O(logk).

Problem G – Gaining Points

ENGLISH

This is a Dynamic Programming question.

The idea is a Min-Max play. While you are trying to maximize your points, your opponent is trying to minimize your points.

For that, we can find a recursive function, where we have the vector V[1..n] with the points:

MaxValue[i,j] = Max(Value[i] + MinValue[i+1,j], Value[j] + MinValue[i,j-1]), if i < j 
MinValue[i,j] = Min(MaxValue[i+1,j], MaxValue[i,j-1]), if i < j
MaxValue[i,j] = V[i], if i == j
MinValue[i,j] = 0, if i == j

Example case 1 from pdf: V = [1, 2, 3, 4]

MaxValue[1,4] = Max(1 + MinValue[2,4], 4 + MinValue[1,3])

MinValue[2,4] = Min(MaxValue[3,4],MaxValue[2,3])
MinValue[1,3] = Min(MaxValue[2,3],MaxValue[1,2])

MaxValue[3,4] = Max(3 + MinValue[4,4], 4 + MinValue[3,3])
MaxValue[2,3] = Max(2 + MinValue[3,3], 3 + MinValue[2,2])
MaxValue[2,3] = Max(2 + MinValue[3,3], 3 + MinValue[2,2])
MaxValue[1,2] = Max(1 + MinValue[2,2], 2 + MinValue[1,1])

MinValue[4,4] = 0
MinValue[3,3] = 0
MinValue[3,3] = 0
MinValue[2,2] = 0
MinValue[3,3] = 0
MinValue[2,2] = 0
MinValue[2,2] = 0
MinValue[1,1] = 0

MaxValue[3,4] = Max(3 + 0, 4 + 0) = Max(3,4) = 4
MaxValue[2,3] = Max(2 + 0, 3 + 0) = Max(2,3) = 3
MaxValue[2,3] = Max(2 + 0, 3 + 0) = Max(2,3) = 3
MaxValue[1,2] = Max(1 + 0, 2 + 0) = Max(1,2) = 2

MinValue[2,4] = Min(4,3) = 4
MinValue[1,3] = Min(3,2) = 2

MaxValue[1,4] = Max(1 + 4, 4 + 2) = 6

But we can see that the time is Exponential.

For that, we do a Memory Matrix to storage the plays while they are calculated, with that we dont have recalculation.

If the play was calculated, then we return it, else we make the processing based on the recurtion.

Time: O(n²).

PORTUGUESE

Esta é uma questão de Programação Dinâmica.

É uma ideia de Mín-Max. Enquanto você está tentando maximizar o seu ganho, o jogador adversário está tentando minimizar o seu ganho.

Para isso podemos achar uma função recursiva, onde temos o vetor V[1..n] com os Pontos:

MaxValor[i,j] = Maior(valor[i] + MinValor[i+1,j], valor[j] + MinValor[i,j-1]), se i < j 
MinValor[i,j] = Menor(MaxValor[i+1,j], MaxValor[i,j-1]), se i < j
MaxValor[i,j] = V[i], se i == j
MinValor[i,j] = 0, se i == j

Exemplo caso 1 do pdf: V = [1, 2, 3, 4]

MaxValor[1,4] = Maior(1 + MinValor[2,4], 4 + MinValor[1,3])

MinValor[2,4] = Menor(MaxValor[3,4],MaxValor[2,3])
MinValor[1,3] = Menor(MaxValor[2,3],MaxValor[1,2])

MaxValor[3,4] = Maior(3 + MinValor[4,4], 4 + MinValor[3,3])
MaxValor[2,3] = Maior(2 + MinValor[3,3], 3 + MinValor[2,2])
MaxValor[2,3] = Maior(2 + MinValor[3,3], 3 + MinValor[2,2])
MaxValor[1,2] = Maior(1 + MinValor[2,2], 2 + MinValor[1,1])

MinValor[4,4] = 0
MinValor[3,3] = 0
MinValor[3,3] = 0
MinValor[2,2] = 0
MinValor[3,3] = 0
MinValor[2,2] = 0
MinValor[2,2] = 0
MinValor[1,1] = 0

MaxValor[3,4] = Maior(3 + 0, 4 + 0) = Maior(3,4) = 4
MaxValor[2,3] = Maior(2 + 0, 3 + 0) = Maior(2,3) = 3
MaxValor[2,3] = Maior(2 + 0, 3 + 0) = Maior(2,3) = 3
MaxValor[1,2] = Maior(1 + 0, 2 + 0) = Maior(1,2) = 2

MinValor[2,4] = Menor(4,3) = 4
MinValor[1,3] = Menor(3,2) = 2

MaxValor[1,4] = Maior(1 + 4, 4 + 2) = 6

Porém vemos que o tempo seria Exponencial.

Para isso fazemos uma Matriz Memória que armazenará nossas jogadas que foram calculadas, e assim não haverá recalculo.

Se a jogada foi calculada, então retornaremos ela, senão faremos o cálculo baseado na recursão.

Tempo: O(n²).

Problem H – Hiperspace

ENGLISH

It is a brute force/implementation question. We just have to make 3 verifications, if n ≤ 299 you show 'Hiperespaco nao esta disponivel', else if n ≤ 499 you show 'Hiperespaco esta disponivel', else you show 'Hiperespaco ativado'.

Time: O(1).

PORTUGUESE

É uma questão de força bruta/implementação. São apenas 3 verificações, se n ≤ 299 você imprime 'Hiperespaco nao esta disponivel', se não, se n ≤ 499, você imprime 'Hiperespaco esta disponivel', senão você imprime 'Hiperespaco ativado'.

Tempo: O(1).

Problem I – Isolated

ENGLISH

This is a search/implementation/brute force question.

Frist we create a binary vector to know if the person is isolated or not.

The size of the vector is n, and we defined: if the person i is isolated the vector[i] is equals to one, otherwise, is equals to zero.

For each person we add him at the vector and compare with the others added previously.

if P₁ interact with P₂, i.e. (P₁.x - P₂.x)² + (P₁.y - P₂.y)² ≤ R², then we mark in teh vector P₁ e P₂ as 0.

At the and we sum all the isolated in the vector and print.

Time: O(n² + n).

PORTUGUESE

É uma questão de busca/implementação/força bruta.

Primeiramente criar um vetor binário para saber quem é isolado ou não.

O tamanho do vetor é n, e definiremos, se o elemento i é isolado, o vetor[i] é igual a um, se não, é igual a zero.

Cada pessoa é adicionada em um vetor, e comparada com as pessoas adicionadas anteriormente.

Se P₁ interage com P₂, ou seja, (P₁.x - P₂.x)² + (P₁.y - P₂.y)² ≤ R², então marcaremos no vetor P₁ e P₂ como 0.

No final somaremos todos os isolados no vetor de isolados e imprimiremos.

Tempo: O(n² + n).

OBS: Esta questão é interessante se pudermos fazer algo utilizando uma busca em profundidade no vetor ou se variarmos o R de interação para cada pessoa, mas para simplificar fizemos o algoritmo quadrático.

Problem J – Zumbie Game

ENGLISH

This is a implementation/grid question. (or just applying math if you want)

The Grid is a matrix where the columns are the number of rounds and the lines the lost health points of the character.

The matrix is filled with zeros.

Initially the Probability of he wins in 0 rounds is 100% (1.0000), because he is not going to lose health.

Grid[0][0] = 1, 0 rounds e 0 health points lost.

We have 2 situations:

1) Win the round.

Win the round have P of probability, soo we get the actual probability multiplied by P and sum to the next round.

Grid[i][r+1] <- Grid[i][r+1] + Grid[i][r]*P

2) Lose the round.

Lose a round have (1 - P) of probability, soo we get the actual probability multiplied by (1–P) and sum for the next round with 1 more of health points lost.

Grid[i+1][r+1] <- Grid[i+1][r+1] + Grid[i][r]*(1-P)

This have to happen if i is less than the max health, because the life cant be zero.

Then we run from the column 0 to R, and propagate from the row 0 to the MaxHealth, analysing. If the next line is zero, then jump to the next column.

At the end, sum the probabilities of the last column, column R, and print. Time: O(MaxHealth*R).

OBS: VidaMáxima means MaxHealth.

At the example case 1 of the pdf. First fill the grid as this:

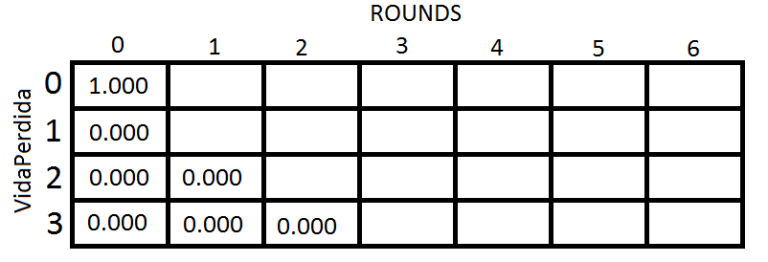
Initialy the Health Point is maximized, then for the [0,0] we have 1.000 of winning. Propagate the Victory and the Defeat.

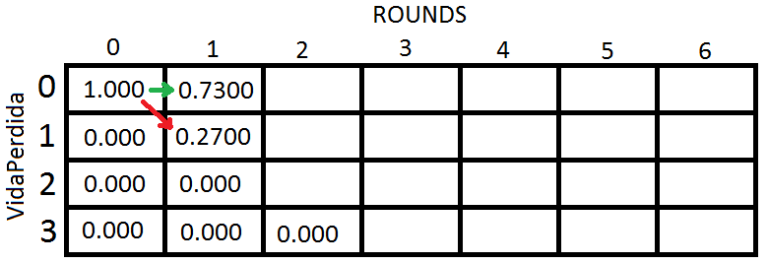
If we look, to win the round 1, we have 100% chance, because we have to lose 4 rounds to lose 4 of health. Completing the Grid:

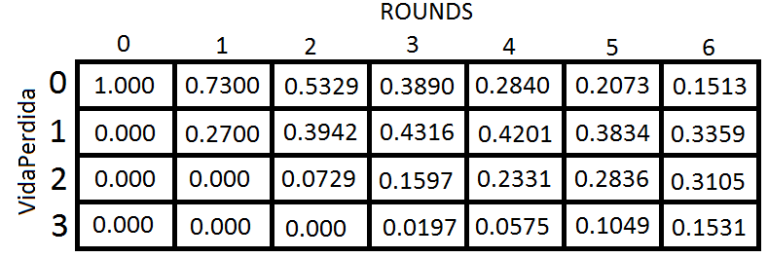
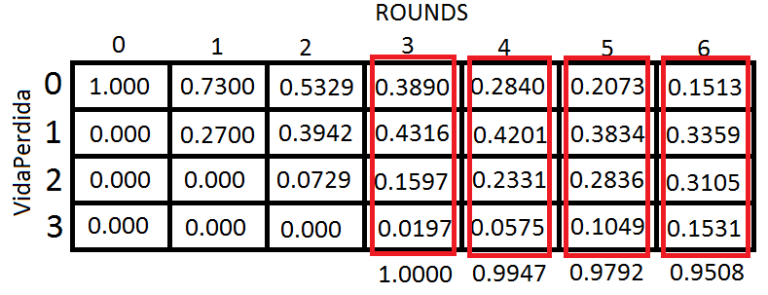
For 6 Rounds, the sum is: 0.9508.

For 5 Rounds, the sum is: 0.9792.

For 4 Rounds, the sum is: 0.9947.

For 3 Rounds, the sum is: 1.0000.

PORTUGUESE

É uma questão que usa uma técnica de programação chamada Grid.

O Grid será uma matriz onde as colunas são o número de rounds e as linhas são os Pontos de Vida que o personagem perdeu.

A matriz será preenchida de zeros.

Inicialmente a Probabilidade dele em 0 rounds é 100% (1.000), pois ele não terá que vencer nada.

Grid[0][0] = 1, 0 rounds e 0 vidas perdidas.

Teremos 2 situações:

1) Vencer o Round.

Vencer um round tem a probabilidade P, então pegaremos a probabilidade atual multiplicada por P e somaremos para o próximo round.

Grid[i][r+1] <- Grid[i][r+1] + Grid[i][r]*P

2) Perder o Round.

Perder um round tem a probabilidade (1 - P), então pegaremos a probabilidade atual multiplicada por (1–P) e somaremos para o próximo round com 1 pontos de vida perdido.

Grid[i+1][r+1] <- Grid[i+1][r+1] + Grid[i][r]*(1-P)

Isto deve acontecer se i é menor que a vida máxima, pois a vida não pode zerar.

Então percorreremos da coluna 0 até R, e propagaremos da linha 0 até Vida máxima, analisando. Se a próxima linha for zero, então pula para a próxima coluna.

No fim, somaremos as probabilidades da última coluna, coluna R, e imprimiremos.

Tempo: O(VidaMaxima * R).

Para o exemplo do caso 1 do pdf. Primeiro preencheremos nosso grid assim:

Inicialmente a vida é máxima, então para vida perdida 0 e round 0 temos 100% chance de ganhar. Então propagamos a Vitória e a Derrota.

Se olharmos, para ganhar no round 1, teremos 100% de chance, pq precisa ter até o 4 round para perder os 4 de vida. Completando o Grid ficará:

Para 6 Rounds, somamos ficaremos com: 0.9508.

Para 5 Rounds, somamos ficaremos com: 0.9792.

Para 4 Rounds, somamos ficaremos com: 0.9947.

Para 3 Rounds, somamos ficaremos com: 1.0000.