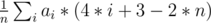- There are n! kinds of paths, ie. n * n! pairs.
- For each ai there are (n - 1)! times being the last one(appear once), And n! - (n - 1)! times appear twice,
- Thus a number ai appear 2 * (n! - (n - 1)!) + (n - 1)! = 2 * n! - (n - 1)! times.
- Realize that among all paths, except for the first row, ie. |0 - ai|, each pair
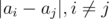 appears (n * n! - (n - 1)!) / C(n, 2) = 2 * (n - 1)! times.
appears (n * n! - (n - 1)!) / C(n, 2) = 2 * (n - 1)! times. - Assume that the squence is sorted in ascending order.
 has i elements less than it. Hence, include the first row it has i * 2 * (n - 1)! + (n - 1)! = (2 * i + 1) * (n - 1)! times to be positive, and has 2 * n! - (n - 1)! - (2 * i + 1)(n - 1)! = 2 * n! - (2 * i + 2) * (n - 1)! to be negative.
has i elements less than it. Hence, include the first row it has i * 2 * (n - 1)! + (n - 1)! = (2 * i + 1) * (n - 1)! times to be positive, and has 2 * n! - (n - 1)! - (2 * i + 1)(n - 1)! = 2 * n! - (2 * i + 2) * (n - 1)! to be negative. - Thus, for each ai, include 1st row, the sum of it in all paths is
7, Average for ai's sum is
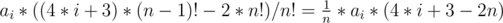
- Finnally, we got the result: