Today I found a problem in XXI Polish OI.

Tourism

But I think it's a NP problem, base on this

I've tried greedy solution, but got 45 points. I'm looking for a solution on Polish OI page but it doesn't have. Someone please help me, thank you.

Given an array A has N integer (1 <= a[i] <= 100, N <= 100) and a number X (X <= 10^9)

Counting number of ways that can get X from a subsequences of A (an element can be used as many as you want)

anyone has a idea for it ?

So the question is above ? I think IDE and Editor are important part too (beside algorithm), it may help you code faster or more "accuracy".

For me, I'm coding pascal and C++, I use Codeblock for C++ and Sublime Text for Pascal, anybody has a greater idea ? :D

In codeforces gym 2014 KTU ACM ICPC Qualification Round, my team MEP was at rank 1.

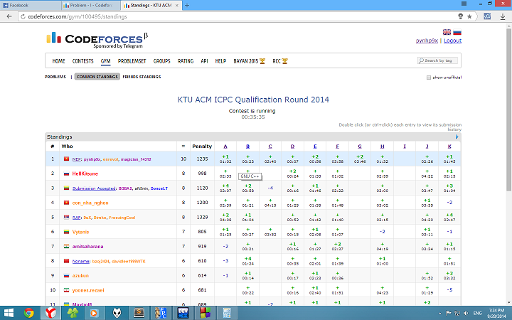
But when gym ended, my team was removed from standing board

http://mirror.codeforces.com/gym/100495/standings

and I've no idea, someone please give me a reason.

Thank you so much.

It's about 2 hours left to 25/9, tourist birthday! Maybe too soon, but happy birthday to you, my idol :D

http://www.spoj.com/problems/TPCPPLAR/

Given a directed graph G = (V,E), N vertices and M arcs. (N <= 150000, M <= 300000)

A node X called "acessable" to Y if there is a path from X to Y

A node X called "popular" if every node Y in V fulfill one of two conditions :

1. X is acessable to Y

2. Y is acessable to X

The Problem : Given graph G, count the number of popular node.

Someone has a solution for this problem.

I used Topo sorting, but I'm stucking at how to check all node previous i can go to i.

Sorry for my bad English.