I wrote in May about the launch of Data Structures and Algorithms Specialization at Coursera. In September, the Advanced Algorithms and Complexity Course of this Specialization was launched, and I'd like to tell you more about it.
Course topics:
- Network Flows (Ford-Fulkerson and Edmonds-Karp algorithms).
- Linear Programming (the Simplex Method).
- NP-completeness (theory, reductions, solving NP-complete problems using SAT-solvers).
- Coping with NP-completeness (bruteforce optimizations, solvable cases, approximation algorithms).
- Streaming Algorithms.
The problems for this course were prepared by ifsmirnov, ilyakor, Michael, Perlik, romanandreev, Zlobober and Paul Melnichuk.
Network flows and the algorithms covered in the Specialization can sound as not very advanced topic for many Codeforcers. On the other hand, it is definitely a popular topic: there is a problem on network flows application virtually in every contest nowadays, and knowing the basic algorithms for finding flows is a must. One of the problems in the Programming Assignment of the Network Flows module supports that: Google Code Jam officially allowed us to use the statement of the problem Stock Charts from GCJ 2009 R2 (ilyakor has prepared the tests and the solutions for our version). Also, it often turns out that you should solve competitive programming problems on flows using Ford-Fulkerson algorithm, because it can be implemented extremely fasta, and it works fast in practice, but for the rare cases when the authors prepared specialized test cases breaking Ford-Fulkerson which is non-trivial.
Linear Programming has never been a competitive programming topic...right until the ACM ICPC World Finals 2016 where problem I just screamed "implement Dijkstra and Simplex Method". In the end, only one team from Stanford University solved this problem, and only two more teams tried. Stanford got lucky: they had the simplex method in their team notebook. However, according to what I observed during the finals as an ICPC analyst, they got unlucky too: it seems their implementation had a bug) As a result, they've spent a lot of time on fixing it and got the problem accepted only during the last hour, although they've started trying much earlier. I might have confused Stanford team's troubles with Wroclaw university's, though — sorry if that's the case. Anyway, so many teams have missed their chance for a much better result! One didn't have to solve anything, just needed to implement two algorithms, one of which many ACM ICPC finalists can implement without opening their eyes at night. romanandreev who prepared the problems on linear programming made sure that his solution passes on the problem I from World Finals 2016. Forums on the Coursera are flooded with discussions of accuracy problems and other subtleties of Simplex Method. Some of the students even complained that they have passed a full separate course just about Linear Programming, and have passed this problem there, but can't pass it in our course :) So you can test your implementation for the team notebook pretty well)
As opposed to competitive programming, in the real life Linear Programming finds lots of applications from optimizing advertising budgets, investment portfolios, diets, transportation, manufacturing, telecommunications to approximation algorithms for NP-hard problems, including the Travelling Salesman Problem.
It might sound surprising, but NP-completeness and coping with it could be seen as the most practical part of the course. You'd argue that this is all about Complexity, but in practice most of the problems are NP-complete and it is much more efficient to see the problem is NP-complete at once and think of ways to cope with that (that's what we talk about in the two modules) instead of trying to come up with some clever data structure, essentially trying to prove P!=NP wrong, without knowing it. Some of the problems use SAT-solver as a checker, because the problem is to reduce the initial problem to a SAT instance, and then it turns out modern SAT-solvers based on the latest research advances can solve huge instances in practice.
Streaming Algorithms are on the rise now, because often in Big Data processing you need to compute some statistic (number of different keys, the most frequent key, estimate the size of intersection of two sets of keys) based on terabytes of data using very limited amount of memory and reading the data just once or maybe twice. We've invited Michael Kapralov to cover this topic. We are going to add a problem on application of streaming algorithms later. It is challenging to separate the Streaming Algorithms from the regular ones under the typical time limits, but we already have a prototype, now it's only left to package what we got into a problem.










 . Otherwise, consider the expected increase in the mood braught by
. Otherwise, consider the expected increase in the mood braught by 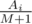 . For candies that are not tasty the expected change in the mood is
. For candies that are not tasty the expected change in the mood is 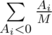 , as each of the not tasty candies can become the first not tasty candy. Overall, the expectation of the mood change is equal to
, as each of the not tasty candies can become the first not tasty candy. Overall, the expectation of the mood change is equal to 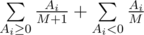 .
.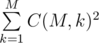 different possible photos.
different possible photos.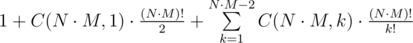 .
.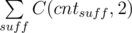 , where the sum is over all suffixes.
, where the sum is over all suffixes.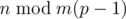 is good. For each
is good. For each 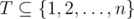 to assistants and he executes the remaining tasks (but not necessarily in consecutive days), then there exists an optimal schedule in which the professor delegates the tasks from
to assistants and he executes the remaining tasks (but not necessarily in consecutive days), then there exists an optimal schedule in which the professor delegates the tasks from 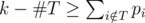 .
.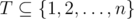 during days after
during days after 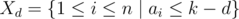 be the set of tasks which can be assigned in day
be the set of tasks which can be assigned in day 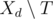 is not empty, then we can in day
is not empty, then we can in day 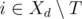 which maximizes the value of
which maximizes the value of 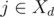 (since assistant will finish before the deadline) and
(since assistant will finish before the deadline) and 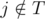 (we assume that
(we assume that 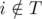 , and
, and 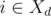 ). Otherwise, if
). Otherwise, if 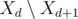 to the heap (i.e. tasks with
to the heap (i.e. tasks with  .
. 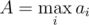 . Adding binary search, we get the solution which works in time
. Adding binary search, we get the solution which works in time 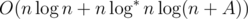 .
. to denote the resulting parts. A solution to this problem can be obtained in three natural steps.
to denote the resulting parts. A solution to this problem can be obtained in three natural steps.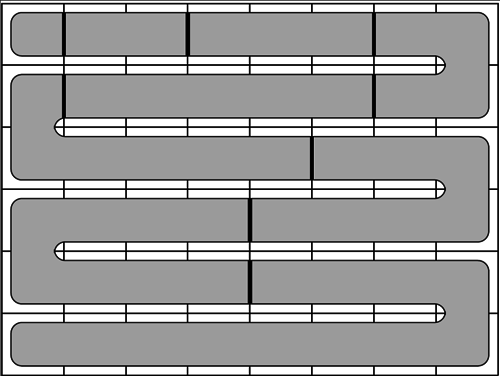
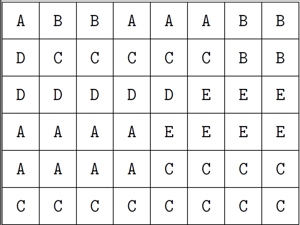
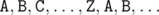 in the order they appear in the snake. However, such a labeling does not work in some cases.
in the order they appear in the snake. However, such a labeling does not work in some cases. time. Let
time. Let 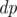 , where
, where 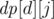 is true if and only if the divisor
is true if and only if the divisor 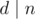 :
: 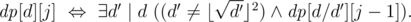
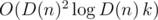 due to a map-like data structure required to keep track of the divisors of
due to a map-like data structure required to keep track of the divisors of 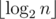 , which in our case is 29. Indeed, for
, which in our case is 29. Indeed, for 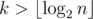 the answer is always “NO” (an argument for this can be inferred from the next solution).
the answer is always “NO” (an argument for this can be inferred from the next solution).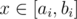 if and only if one can take
if and only if one can take 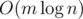 time.
time.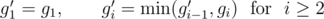
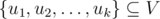 and a moment of time, check whether these nodes form one or more whole connected components of the graph in this moment of time.
and a moment of time, check whether these nodes form one or more whole connected components of the graph in this moment of time.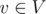 we store in
we store in 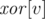 the
the 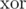 -product of weights of all edges that are adjacent to this node. Note that such values can be updated in
-product of weights of all edges that are adjacent to this node. Note that such values can be updated in 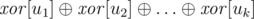
 denotes the
denotes the 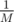 where
where  the same number, but when we allow stickers to overflow and cover positions from
the same number, but when we allow stickers to overflow and cover positions from  stickers.
stickers.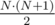 .
. . There is a fast method to compute
. There is a fast method to compute 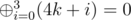 . Thus
. Thus 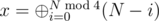 .
. . So, if we are able to make the first move from group
. So, if we are able to make the first move from group 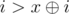 . It is only possible if at position
. It is only possible if at position 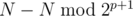 exactly half are such
exactly half are such 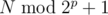 should be added to the answer.
should be added to the answer.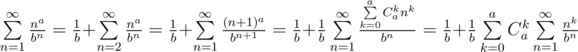
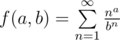 , we get
, we get 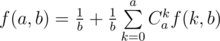
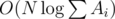 . We should also note that one has to initially sort topics by value of
. We should also note that one has to initially sort topics by value of 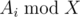 to search for topics with the maximum number of problems to solve when Gennady can't solve
to search for topics with the maximum number of problems to solve when Gennady can't solve 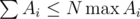 and properties of
and properties of 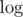 we get complexity
we get complexity 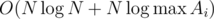 .
.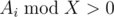 .
. .
.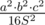 .
. 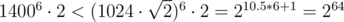 , so it fits into unsigned int64. To compare such fractions one has to either use long arithmetics or use modular arithmetics or compute GCD or store high-order number part separately...
, so it fits into unsigned int64. To compare such fractions one has to either use long arithmetics or use modular arithmetics or compute GCD or store high-order number part separately...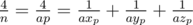 . So it is sufficient to precalculate answers for all prime
. So it is sufficient to precalculate answers for all prime 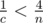 , then
, then 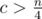 . As
. As 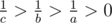 , so
, so 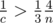 and
and 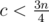 . Using the same logic
. Using the same logic 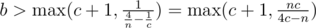 and
and 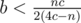 . So, let us bruteforce through all prime
. So, let us bruteforce through all prime 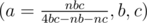 .
. as a sum of two "egyptian" fractions using Fibonacci's algorithm. This solution passes the Time Limit without precalc.
as a sum of two "egyptian" fractions using Fibonacci's algorithm. This solution passes the Time Limit without precalc.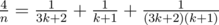 ,
,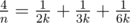 ,
,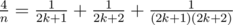 ,
,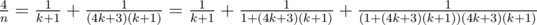 ,
,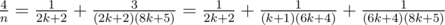 .
. in increasing order manages to pass in under a second. The following function in C/C++ must be run as
in increasing order manages to pass in under a second. The following function in C/C++ must be run as 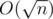 time. Also we can first decompose
time. Also we can first decompose 








