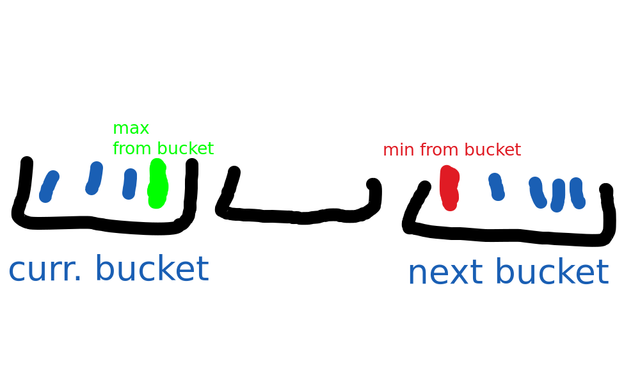
A few days ago, someone much smarter than me shared with me the following problem. He said it involves "nothing else but simple arrays and for-loops, but has some weird observations to make". I couldn't solve it, even though the solution is simple enough that it can probably be understood by higher-rated pupils on CF. I thought it might be interesting to you, so here it is:
You are given an array $$$a$$$ with $$$n$$$ positive integers (you don't know anything about their maximum value). Find out the maximum difference between two elements if the array $$$a$$$ would be sorted.
Example:
Input: $$$n = 4, a = [11, 2, 7, 5]$$$
Output: $$$4$$$, because if we were to sort the array $$$a$$$, then we would have $$$[2, 5, 7, 11]$$$, so the maximum difference between two adjacent elements is $$$4$$$.
Of course, you can just sort the array in $$$O(n \log n)$$$ and find the difference that way. Value-based sorting (like radix sort) is not an option because you don't know what the maximum value is. But there is actually a way to find it in $$$O(n)$$$, without sorting the array.
Hope you enjoyed the problem!