I'd like to offer you two chess problems.
In both problems there is checkmate in 1, white to play.
If you think that any fool can solve checkmate in 1, these positions are for you!

Please post your answers under spoilers!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 2 | maomao90 | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
I'd like to offer you two chess problems.
In both problems there is checkmate in 1, white to play.
If you think that any fool can solve checkmate in 1, these positions are for you!

Please post your answers under spoilers!
At first I tell about the contest at all.
And now let's start analysis.
Problem A (div.2) - Restoring Password
Password was very easy to restore. You should just iterate over groups of 10 characters in the first string and over all codes. Then, if some number's code is equal to the group - print that number.
Here's the example: http://pastebin.com/hMV0NcjN
Problem B (div.2) - Friends
Let's construct the graph where vertices correspond to the people and edges correspond to the relationships. Then paint each edge in this way: edge will be red if the men connected by it are friends and black otherwise. Now let's think what is "three pairwise acquainted people" and "three pairwise unacquainted people". We see that they are cycles of only red and only black vertices correspondingly, and the length of these cycles is 3.
Now we know the solution: write 3 "for" cycles, one cycle for one vertex, and check if the edges between these vertices are only red or only black.
Here's the solution: http://pastebin.com/gswaxGmM
Another way to solve it is to notice the answer is FAIL if and only if graph has exactly 5 edges and they all together form a cycle with a length 5. It's very funny solution, I think. Here's the code: http://pastebin.com/09T0ixrJ
Problem A (div.1) / C (div.2) - Frames
The best way is to find all cases with answer 1 and 2. Try to do it.
If the answer is 1, we can select all folders from a to b with one selection. There must be nothing hard to detect these cases:
And these are the cases with answer 2:
If no one of these conditions is true, answer is 3.
Here's the solution: http://pastebin.com/8QRytzzF
Problem B (div.1) / D (div.2) - End of Exams
Greedy algorithm solves this problem. We should consecutively try to pour milk from each bottle into each available cup and in maximal possible amount.
Also we always need to know, how much milk is in each bottle and each cup, for each cup - bottles from which we have poured milk, and for each bottle - cups into which we have poured milk.
Writing it is not hard. But where is one special moment - if we compare real numbers, we must use EPS, or we can get WA on test 12 (50 1000 49). Some programs write NO on this test while answer is YES, because of wrong comparing of real numbers.
It must be said that answer can be calculated in integers: just set the volume of milk in each bottle mn. And only when we will print the answer, we divide each volume by mn and multiply by w. All three jury solutions didn't think up this :)
Problem C (div.1) / E (div.2) - Azembler
I don't know why so few coders have solved it. Small limitations for n and big time limit - 5 seconds - hint that it's backtracking. Also, no need to be a soothsayer to understand that maximal answer is about 5.
Solving it is clear. You should keep all current registers at the vector and call some function that goes over all current registers and calculate new values, then calls itself recursively. In that process we can also save the program itself.
Problem D (div.1) - Flags
I think my solution is not optimal, it's too long. Many solutions submitted during the contest are shorter. But I tell you about my solution.
At first I solve the problem for the number of stripes equals N (or L = R).
Let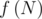 is the number of flags with exactly N stripes where symmetrical flags are not identical. Try to get the answer using this designation.
is the number of flags with exactly N stripes where symmetrical flags are not identical. Try to get the answer using this designation.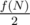 . But it's not true for the palindromes. For example, for non-palindromes WBWB and BWBW we should count only one of them, but for the palindromes, such as WBW, it leads to mistake, because each palindrome is symmetrical to itself.
. But it's not true for the palindromes. For example, for non-palindromes WBWB and BWBW we should count only one of them, but for the palindromes, such as WBW, it leads to mistake, because each palindrome is symmetrical to itself.So for the flags with even number of stripes formula 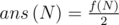 is correct, because there are not palindromes among them. And if N is odd, the correct formula is
is correct, because there are not palindromes among them. And if N is odd, the correct formula is 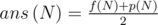 , where
, where 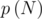 is the number of palindromes with N stripes. Each palindrome is definited by its first
is the number of palindromes with N stripes. Each palindrome is definited by its first 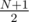 stripes, and we can write that
stripes, and we can write that 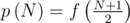 .
.
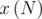 with a length 8 where each its component keeps a number of flags with N stripes and definite two last colors (exactly 8 options). And
with a length 8 where each its component keeps a number of flags with N stripes and definite two last colors (exactly 8 options). And 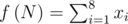 is total number of flags with N stripes.
is total number of flags with N stripes.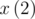 which consists of ones (because there are 8 flags with a length 2, one flag for one possible combination of two colors). And how to calculate
which consists of ones (because there are 8 flags with a length 2, one flag for one possible combination of two colors). And how to calculate 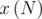 ?
?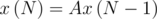 . Its elements can be found even using pen and paper: for example, let's we have a combination of two last stripes WB. Then it's possible to add white or yellow stripe to the end, and the last stripes will be BW and BY correspondingly. It means that we can write 1 to the matrix where the row are BW or BY and the column is WB.
. Its elements can be found even using pen and paper: for example, let's we have a combination of two last stripes WB. Then it's possible to add white or yellow stripe to the end, and the last stripes will be BW and BY correspondingly. It means that we can write 1 to the matrix where the row are BW or BY and the column is WB.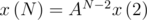 . Power of matrix can be calculated with a logarithmic time - that's because our problem is solved. And don't forget if N = 1 then answer is 4 and there's no need to do these calculations.
. Power of matrix can be calculated with a logarithmic time - that's because our problem is solved. And don't forget if N = 1 then answer is 4 and there's no need to do these calculations.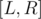 .
. (if L = 1, we can write "if" somewhere at the beginning of the program). And the matrix A should be changed a bit: try to do it by yourself.
(if L = 1, we can write "if" somewhere at the beginning of the program). And the matrix A should be changed a bit: try to do it by yourself. . It is equal to
. It is equal to 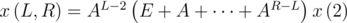 . Let's learn how to calculate the sum E + A + ... + AN quickly.
. Let's learn how to calculate the sum E + A + ... + AN quickly.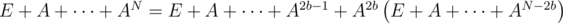 .
.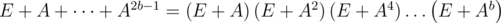 . And the expression in the brackets at the second part of that formula is... I think you've already understood it :)
. And the expression in the brackets at the second part of that formula is... I think you've already understood it :)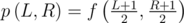 .
.This problem can be solved using inclusion-exclusion principle. If 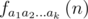 is the answer, then the following formula works:
is the answer, then the following formula works: 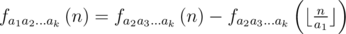 . But if you write only this recursive function, you get TLE. Many contestants got TLE and were hacked because they didn't run maximal test on their computers.
. But if you write only this recursive function, you get TLE. Many contestants got TLE and were hacked because they didn't run maximal test on their computers.
And the others who sensed that something was wrong memorized the answers for small n and all ai. For example, you can see solution by rng_58 who won the contest, or this solution: http://pastebin.com/4kcfJdAi.
Hi all!
My name is Alexey Dergunov, and I'm glad to present you the first "violet" Codeforces round. I hope the problems will not seem so "violet" to you :)
Many thanks to following people who helped me a lot with contest preparation:
| Name |
|---|


