Ever since I read this blog, I have been curious to see how space-filling curves other than Hilbert can be used to reduce the run time. In this blog, we will see how Peano curves can help bring down the run time of Mo's algorithm-based solutions. Peano curve generalizes very easily to higher dimensions, so it's worth using for problems based on Mo's algorithm with updates.
Prerequisites: Mo's algorithm, Mo's algorithm using Hilbert Curve order, Mo's algorithm with updates
Relation with TSP
In Mo's algorithm, we try to come up with a comparator that can help us sort the queries in such a way that minimizes the total movement of L and R pointers. In other words, if we have $$$Q$$$ queries, each of the form $$$l_i$$$, $$$r_i$$$, then we wish to find such an arrangement of the queries that minimizes the following summation:
$$$S = \displaystyle\sum_{i=1}^{Q-1} |l_i - l_{i+1}| + |r_i - r_{i+1}|$$$.
Each query $$$(l,r)$$$ can be viewed as a coordinate on a 2D plane. We want to visit each of these points such that the travelled distance (with Manhattan distance as the distance metric) is minimized. This problem is the same as Traveling Salesman Problem (TSP), but a variant in which the salesman does not need to return to the starting city / point.
This problem is NP-Hard, taking exponential time to find the best minimum cost. However, we can trade-off time with accuracy. We can find a good enough solution which takes polynomial time and is fast enough. This is what space-filling curve based heuristic solutions help us achieve. Since the summation minimization problem is the same as TSP, we can apply the same heuristic approaches to Mo's algorithm. Let's try to find a new comparator based on all this information.
New Comparator
A comparator that uses Hilbert curve order has already been explained in this blog quite nicely. Here I will discuss a comparator that uses Peano curve order.
Let's build a Peano curve on a $$$3^k × 3^k$$$ matrix and visit all the cells on the matrix according to this curve. Denote ord(i, j, k) as the number of cells visited before the cell (i, j) in order of Peano curve on the $$$3^k × 3^k$$$ matrix. We sort the queries in non-descending order w.r.t. their value of ord(i,j,k).
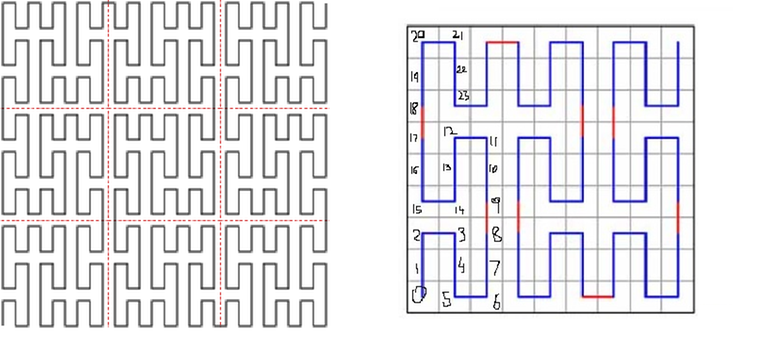
Butz gives an algorithm for computing the Peano space-filling curve in terms of the base-3 representation of coordinates. It generalizes pretty well with higher dimensions. I will describe the algorithm briefly, assuming a point in an n-dimensional plane.
List down the coordinates in base 3 representation. Each coordinate takes up k places in the base 3 / ternary representation. Here, we choose k such that k satisfies $$$3^k \geq N$$$ (N is the maximum value a coordinate can take).
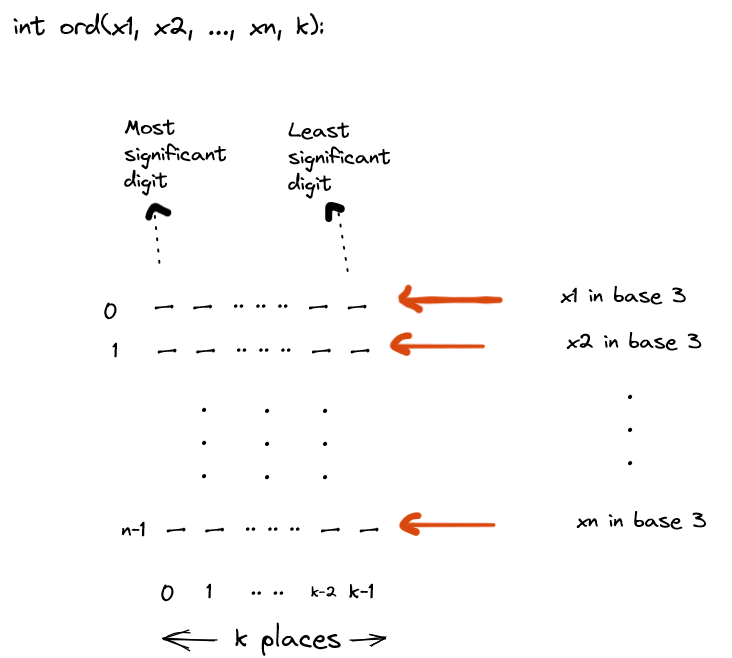
Each row is a coordinate, taking up k places to write in ternary form (leading zeroes allowed). Let this matrix formed be denoted by $$$a$$$
Perform $$$\text{peano-flip}$$$ on each $$$a_{i,j}$$$. It is a function that modifies $$$a_{i,j}$$$ values.
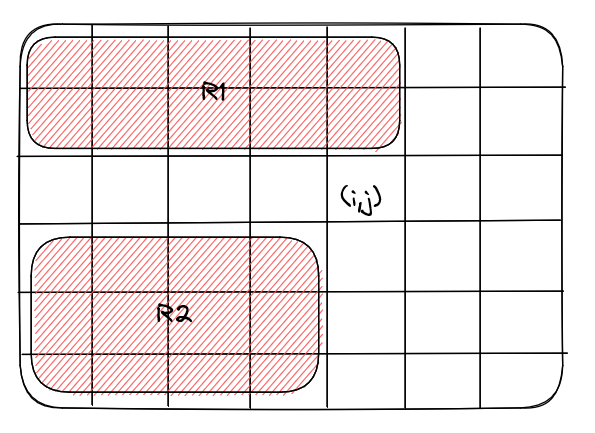
$$$R1$$$ corresponds to the rectangle with (0, 0) and (i-1, j) as the upper left and lower right corners respectively.
$$$R2$$$ corresponds to the rectangle with (i+1, 0) and (n-1, j-1) as the upper left and lower right corners respectively.
If $$$R1 + R2$$$ is odd, do: $$$a_{i,j} = 2 - a_{i,j}$$$
Else we do nothing.Let ord(i,j,k) = num. Then, num is obtained by constructing a number off $$$a_{i,j}$$$ in base 10 in the following way:
For example, let's find Peano order for the query (1, 3). We can choose k = 2 as $$$3^2 \geq 8$$$.
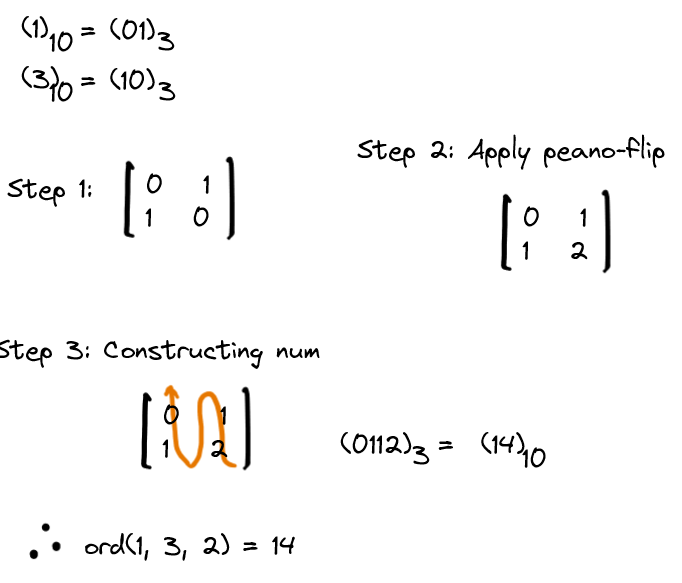
You can verify from the peano order diagram that (1, 3) corresponds to 14 (assuming 0 based indexing).
Here is an implementation of Peano order for our 2 dimensional queries:
We can take k = 13 for all practical reasons, as $$$3^{13} \geq 10^{6}$$$
Time complexity using Peano order is $$$O(N \sqrt{Q})$$$. The proof is almost identical to this blog.
Suppose we have $$$n = 3^k$$$ and $$$q = 9^l$$$, where k and l are some integers. (If n and q are not powers of 3 and 9 respectively, we increase them, it doesn't have any effect on asymptotic). Now divide the matrix onto squares with size $$$3^{k-l} × 3^{k-l}$$$. To travel between a pair of adjacent squares, we need $$$O(3^{k-l})$$$ time, so we can travel between all the squares in $$$O(3^{k-l}\cdot 9^l) = O(3^{k+l}) = O(n \sqrt{q})$$$ time. Now consider the groups of queries inside a $$$3^{k-l} × 3^{k-l}$$$ square. Here we can travel from one query to another in $$$O(3^{k-l})$$$, so we process all such groups of queries in $$$O(q \cdot 3^{k-l}) = O(q \cdot \frac{n}{\sqrt{q}}) = O(n \sqrt{q})$$$ time. So the total time to process all the queries is $$$O(n \sqrt{q}).$$$
Use in problems
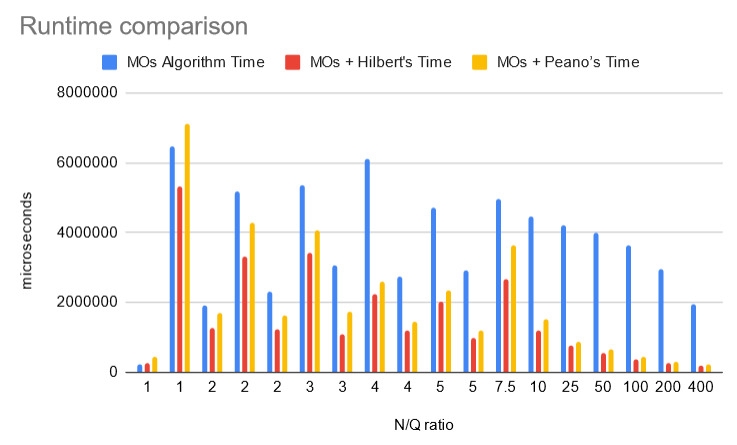
But how does Peano order compare with Hilbert order and the canonical version? In general, Hilbert > Peano > Canonical Here are some benchmarks:
| Test Number | N/Q | MOs Algorithm Time | MOs + Hilbert's Time | Time Ratio (Canonical / Hilbert) | MOs + Peano’s Time | Time Ratio (Canonical / Peano) |
|---|---|---|---|---|---|---|
| 1 | 1 | 248000 | 268035 | 0.925 | 436000 | 0.569 |
| 2 | 1 | 6460207 | 5328098 | 1.212 | 7123959 | 0.907 |
| 3 | 2 | 1923670 | 1254450 | 1.533 | 1694418 | 1.135 |
| 4 | 2 | 5187390 | 3321519 | 1.562 | 4279745 | 1.212 |
| 5 | 2 | 2293648 | 1235349 | 1.857 | 1614162 | 1.421 |
| 6 | 3 | 5359898 | 3429162 | 1.563 | 4068005 | 1.318 |
| 7 | 3 | 3076011 | 1100197 | 2.796 | 1728999 | 1.779 |
| 8 | 4 | 6096000 | 2233634 | 2.729 | 2588819 | 2.355 |
| 9 | 4 | 2734815 | 1201251 | 2.277 | 1451503 | 1.884 |
| 10 | 5 | 4728829 | 2034390 | 2.324 | 2343998 | 2.017 |
| 11 | 5 | 2928129 | 994038 | 2.946 | 1206444 | 2.427 |
| 12 | 7.5 | 4975073 | 2651273 | 1.876 | 3635598 | 1.368 |
| 13 | 10 | 4456694 | 1212675 | 3.675 | 1517397 | 2.937 |
| 14 | 25 | 4208660 | 778808 | 5.404 | 879259 | 4.787 |
| 15 | 50 | 3988436 | 545145 | 7.316 | 655212 | 6.087 |
| 16 | 100 | 3639918 | 382166 | 9.524 | 433495 | 8.397 |
| 17 | 200 | 2955605 | 263269 | 11.227 | 302042 | 9.785 |
| 18 | 400 | 1956763 | 182696 | 10.71 | 220000 | 8.894 |
An example submission that uses Peano order: https://cses.fi/paste/716421c81ec746975af8b3/
Peano isn't that far off Hilbert. Still, Hilbert order gives the best result.
However, since Peano curves are very easy to generalize to higher dimensions, we can use them in Mo's algorithm with updates. We can represent a query in the form $$$(L, R, T)$$$, where
L = left boundary of the query
R = right boundary of the query
T = Time or Number of updates that happen before this query
Each query can now be thought of as a coordinate in 3D plane. It's the same TSP variant problem but now in 3 dimensions. Using Butz algorithm, we can find the order for (L,R,T) queries.
I tried Peano order for Mo's with update and it halved the runtime.
Example submissions:
1. Problem, Canonical (1466 ms), Mo's with Peano (780 ms)
2. Problem, Canonical (1.94 s), Mo's with Peano (1.01 s)
I hope with Peano order, you can cheese Mo's with updates solution in the Time Limit :D
Thanks to nor for proof-reading the blog. I hope to improve the benchmarks soon!