我們發現中文有一些顯示問題,之後會再處理。 The Chinese version has some display issue with latex for now.
A. Numbers
If D > 0, then there are at most D - 1 integers between the X-th largest integer and the X-smallest integer. So the answer would be 2X + D - 1. If D = 0, then the X-th largest integer is the exactly same integer as the X-smallest integer. So the answer is 2X - 1. If D < 0, then the case with the largest number of integers would be: the X-smallest integer is the very next integer larger than the X-largest integer if sorted ascendingly. So the answer would be 2X - 2.
Overall, the answer can be expressed as 2X + max(D - 1, - 2). Time complexity is O(1).
如果 D > 0,則第 X 大的數跟第 X 小的數之間最多有 D - 1 個數字。所以答案為 $2X + D — 1$。 如果 D = 0,則第 X 大的數跟第 X 小的數其實是同一個數字。所以答案為 $2X — 1$。 如果 D < 0,則最多數字的情況為:如果由小到大排序後,第 X 小的數恰好排在第 X 大的數之後。所以答案為 $2X — 2$。
整體而言,答案可以寫成 $2X + \max(D — 1, -2)$。時間複雜度為 $O(1)$。
B. Power
There are at most 106 discrete time in the logs so if we can find out how many computers are in use at each time, we can calculate the final answer by summing the cost at each time in O(106) time. In order to find out that number, we could scan through the log and accumulate the number of on events and off events at each time which takes O(n) time. After that, just simulate those events time by time to get the number of computers in use at each time.
Time complexity is O(n + max(t)).
時間的最大值為 106,也就是說如果我們可以對每個時間點找出有幾台電腦正在運作中,就可以把每個時間點的花費加總起來而得到最終答案。找出每個時間點有幾台電腦正在運作中的方法為,用 O(n) 的時間掃描一次紀錄檔,並且統計每個時間點開機了幾次跟關機了幾次。之後就可以按照時間模擬這些開關機的事件以求出對於毎個時間有多少台電腦正在運作。
時間複雜度為 $O(n + max(t))$。
C. Robot and Maze
In a word, depth first search. But watch out for stepping into visited blocks to avoid looping. Moreover, you need to issue a command to go back to the previous block in the calling stack. You can use no more than answer × 4 moving commands to solve this task.
Time complexity is O(answer).
簡而言之,深度優先搜尋(DFS)。必須注意的點是,避免重複踏入相同的格子內造成迴圈。另外,在返回上一層函式的同時必須命令機器人移動一次回到上一層的位置。你可以只使用 answer × 4 次移動命令來解這一題。
時間複雜度為 $(answer)$。
D. Combination
Firstly, you have to use inverse modular to deal with the division in the calculations. The combination function is straight forward but there are cases that the C(a + k, b + k) would become 0 for some intermediate values of k because of the modular operation. One way to handle this is to maintain the current C(a + k, b + k) using the form px × r where x is the largest possible integer. If x = 0 we know C(a + k, b + k) = r mod p, otherwise we know C(a + k, b + k) = 0 mod p.
Let's consider a scenario to illustrate the meaning of x. The task is to maintain the value n mod 3 with multiple and division operations. Initially n = 2 and the operations are 1.) multiply by 3 then 2.) divide by 3. If we just simulate each step, we would have n = 0 when the first operation is applied and never recover the true value after the second operation. So, with x, we would have x = 0, n = 2 initially. After the first operation we would have x = 1, n = 2. Since x ≠ 0 so we would know the answer is 0 now. After the second operation, we would have x = 0, n = 2 which preserves the truth that the answer is 2.
When maintaining C(a + k, b + k). There are two operations: multiple and division. To multiple by v, first we find x', r' such that v = px' × r', then do x = x + x', r = r × r'. To divide by v, first we find x', r' such that v = px' × r', then do x = x - x', r = r × modularinverse(r').
Time complexity is 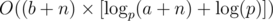 .
.
首先,你必須使用 inverse modular 去處理除法的問題。計算組合的方法很直覺,但是這題中會有一些情況下,$C(a + k, b + k)
Unable to parse markup [type=CF_TEX]
值因為取餘數的關係會變成 0。一個處理的方法為,用 px × r (x 是最大可能的整數) 的形式紀錄 C(a + k, b + k) 的值。如果 x = 0 我們有 $C(a + k, b + k) = r\ mod\ p$,否則有 $C(a + k, b + k) = 0\ mod\ p$。時間複雜度為 $O((b + n) \times [\log_p(a+n) + \log(p)])$。
E. Disk Raid
The key is to use matrix operations inside a segment tree (or similar data structures). In a segment tree, each node will be associated with a range [L, R]. In each node, we store a vector V of size 1 × (n + 1) where the element at position i for 0 ≤ i < n is the sum of the disk values in the range (i.e. 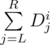 ) and the last element is the size of the range (i.e. R - L + 1). Each operation can be applied to such vector by a matrix multiplication V' = V × Mop. We'll describe how to construct such matrix for each operation below. Here we take n = 2 as example.
) and the last element is the size of the range (i.e. R - L + 1). Each operation can be applied to such vector by a matrix multiplication V' = V × Mop. We'll describe how to construct such matrix for each operation below. Here we take n = 2 as example.
這題的關鍵為在 segment tree (或類似的結構裡) 使用矩陣運算。在 segment tree 中,毎一個 node 代表一個範圍 [L, R]。在每一個 node 裡面,我們存一個 1 × (n + 1) 的 vector V,V 中位置 i (0 ≤ i < n) 的元素為範圍內硬碟 i 的值的總和 (也就是 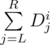 )),而最後一個元素的值為範圍的大小 (也就是 R - L + 1)。毎一個操作都可以看作為一次矩陣乘法 V' = V × Mop。下面我們會描述要如何構造這些矩陣,以 n = 2 為例。
)),而最後一個元素的值為範圍的大小 (也就是 R - L + 1)。毎一個操作都可以看作為一次矩陣乘法 V' = V × Mop。下面我們會描述要如何構造這些矩陣,以 n = 2 為例。
Copy operation from disk 0 to disk 1: Copy 操作,從硬碟 0 到硬碟 $1$:
1 1 0
0 0 0
0 0 1
Modify operation for disk 0: Modify 操作,對於硬碟 $0$:
p1 0 0
0 1 0
p2 0 1
AdvancedModify operation reading from disk 0 and writing to disk 1: AdvancedModify 操作,從硬碟 0 中讀取,寫入硬碟 $1$:
1 p 0
0 1 0
0 0 1
Swap operation for disk 0 and disk 1: Swap 操作,交換硬碟 0 跟硬碟 $1$:
0 1 0
1 0 0
0 0 1
Using the 32-bit unsigned integer data type would solve the modular issue natively. Time complexity is 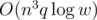 .
.
使用 32 位元的無號整數資料結構可以解決取餘數的問題。時間複雜度為 $O(n^3q\log w)$。








 time. But what if I ask you to output the exact answer (in the form of division of two integers
time. But what if I ask you to output the exact answer (in the form of division of two integers 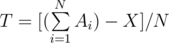 , then verify if
, then verify if 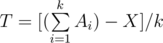 where
where 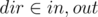 and
and 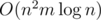 .
. stands for real division.
stands for real division.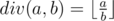 .
.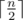 , so the problem equals to determine the minimal integer that is a multiple of m in the range
, so the problem equals to determine the minimal integer that is a multiple of m in the range 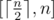 .
.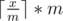 , we can compare this number to the upper bound n to determine if there is a valid solution.
, we can compare this number to the upper bound n to determine if there is a valid solution.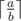 can be calculated in the following c++ code if
can be calculated in the following c++ code if 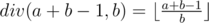
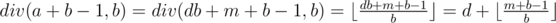 .
.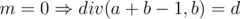 , otherwise
, otherwise 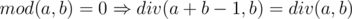 , otherwise
, otherwise 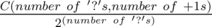 .
.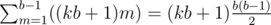 .
.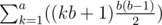 which can be calculated in
which can be calculated in 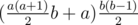 . Dreamoon says he's too lazy to do this part, so if you use
. Dreamoon says he's too lazy to do this part, so if you use 
