Problem Statement

In this challenge, you are given a tree with nodes coloured as red or black and your goal is to change the colour of all the nodes as described.

Given a tree of tree_nodes vertices numbered from 1 to tree_nodes and rooted at vertex 1. Initially, all the vertices except 1 are coloured red. Vertex 1 is coloured black.

• Select any red vertex adjacent to at least one of the black-coloured vertices and change the colour of that selected vertex to black. If there are multiple such vertices, choose any one of them.

Find the number of ways to change and colour all the tree vertices into black. Since this number can be large, return it modulo 10^9 + 7.

Note: Two ways are considered different if the nodes coloured in the ith step is different in the two ways.

For Example: Given tree_nodes = 4, tree_from[1, 1, 2], tree_to = [2, 3, 4]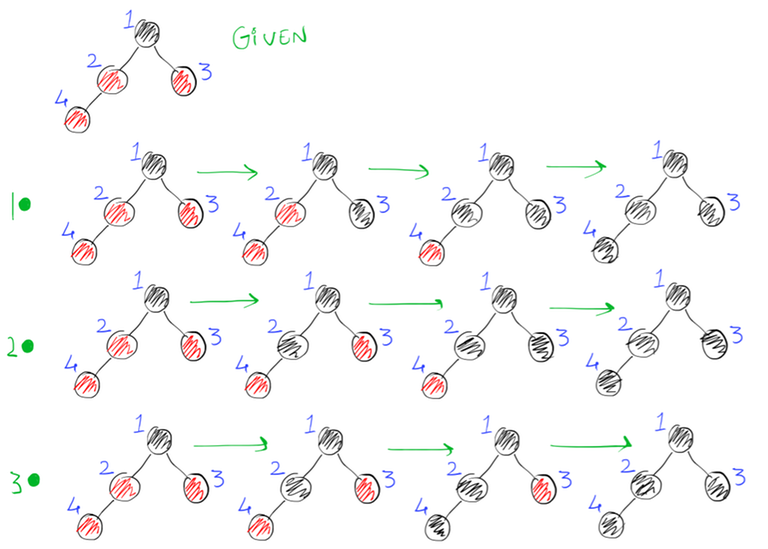
1. Change the colour of vertex 3 to black(since vertex 1 is already black). Now, change the colour of vertex 2 to black (since vertex 1 is already coloured black). And finally, change the colour of vertex 4 to black(since vertex 2 is already coloured black).

2. Change the colour of vertex 2 to black(since vertex 1 is already black). Now, change the colour of vertex 3 to black (since vertex 1 is already coloured black). And finally, change the colour of vertex 4 to black(since vertex 2 is already coloured black).

3. Change the colour of vertex 2 to black(since vertex 1 is already black). Now, change the colour of vertex 4 to black (since vertex 2 is already coloured black). And finally, change the colour of vertex 3 to black(since vertex 1 is already coloured black).

Hence answer is 3.

Constraints:

2 <= tree_nodes <= 10^5
1 <= tree_from <= tree_nodes
1 <= tree_to <= tree_nodes

I was thinking a lot about this problem but didn't get the correct idea.
Please share your ideas via comments. Thank You <3