Блог пользователя c0d3junki3

Precalculating phi function 1..N
Автор c0d3junki3, 11 лет назад, По-английски

http://www.spoj.com/problems/ETF/

Is there an O(N) method to calculate phi functions of all the numbers from 1 to N? I swear, i saw a post here on codeforces about it, but i just can't seem to find it.

Anyway i used the fact that 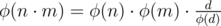where d = gcd(n, m) + a sieve to solve the above problem in 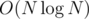, is it possible to do it in O(N)?

  • Проголосовать: нравится
  • +13
  • Проголосовать: не нравится

»
11 лет назад, # |
  Проголосовать: нравится +1 Проголосовать: не нравится 
//Linear sieve algo from http://e-maxx.ru/algo/prime_sieve_linear with this feature

const int N = 10000000;
int lp[N + 1];
int phi[N + 1];
vector<int> pr;

void calc_sieve()
{
    phi[1] = 1;
    for (int i = 2; i <= N; ++i)
    {
        if (lp[i] == 0)
        {
            lp[i] = i;
            phi[i] = i - 1;
            pr.push_back(i);
        }
        else
        {
            //Calculating phi
            if (lp[i] == lp[i / lp[i]])
                phi[i] = phi[i / lp[i]] * lp[i];
            else
                phi[i] = phi[i / lp[i]] * (lp[i] - 1);
        }
        for (int j = 0; j < (int)pr.size() && pr[j] <= lp[i] && i * pr[j] <= N; ++j)
            lp[i * pr[j]] = pr[j];
    }
}
→ Ответить
  • »
    »
    9 лет назад, # ^ |
      Проголосовать: нравится +3 Проголосовать: не нравится

    Thanks a lot dude I used your technique for various problems involving totient functions

    → Ответить
»
11 лет назад, # |
← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

Do you know how to find the smallest prime divisor of each number in O(N)? If don't, please read this (in Russian, but Google Translate works well).

But if you know the smallest prime divisor, the solution is easy. You just need to precalculate the power of this factor and use it for phi calculation. If something is still unclear, please look at this pseudocode:

if (smallest_prime[i] == smallest_prime[i / smallest_prime[i]]) {
    prime_pow[i] = prime_pow[i / smallest_prime[i]] * smallest_prime[i];
} else {
    prime_pow[i] = smallest_prime[i];
}
phi[i] = phi[i / prime_pow[i]] * (prime_pow[i] - prime_pow[i] / smallest_prime[i]);

UPD. Oh, I didn't notice the comment above.

→ Ответить
»
11 лет назад, # |
← Rev. 5   Проголосовать: нравится 0 Проголосовать: не нравится

if(Smallest_Prime[i]==0) Phi[i]=i-1

I get this part. If i is a prime number then Phi[i] must be i-1 (As all the number from 1..to i-1 are relative prime to i ).

But I am confused with this part


else
        {
            //Calculating phi
            if (lp[i] == lp[i / lp[i]])
                phi[i] = phi[i / lp[i]] * lp[i];
            else
                phi[i] = phi[i / lp[i]] * (lp[i] &mdash; 1);
        }

Let i = 8, then according to the code blocked above, if(lp[i] == lp[ i/lp[i] ]) this part is true (As lp[8] == 2 and lp[4] == 2 also ) then we are putting phi[i] = phi[i / lp[i]] * lp[i]; What is the prof of that?

Please Someone help .. Thank You :)

→ Ответить
  • »
    »
    11 лет назад, # ^ |
    ← Rev. 5   Проголосовать: нравится +2 Проголосовать: не нравится

    You can get it from the formula for PHI:

    PHI [n] = n * (1 - 1/p1) * (1 - 1/p2) * ... * (1 - 1/pn) where p1,p2.. pn are the prime factors of n.

    Say we know the smallest prime factor of n, that is lp [n]. What is the formula for n/lp[n] ? Well there are two cases:

    1) n/lp[n] is still divisible by lp[n], that is lp[n] is a factor of n with a power greater than or equal to 2, so n/lp[n] has exactly the same prime factors as n.

    Then PHI[n/lp[n]] = (n/lp[n]) * (1 - 1/p1) * (1 - 1/p2) * ... * (1 - 1/pn) It differs from the above formula by the first term. So just multiply phi[n/lp[n]] by lp[n] to get phi[n]. PHI[n] = PHI[n/lp[n]] * lp[n]

    2) n/lp[n] is not divisible by lp[n], then the above formula for n/lp[n] is almost the same, it just doesn't have (1 — 1/lp[n]) as one of its terms. So we have to multiply phi[n/lp[n]] not only by lp[n] but also by (1 — 1/lp[n]).

    Then PHI[n] = PHI[n/lp[n]] * lp[n] * (1 - 1/lp[n]] => PHI[n] = PHI[n/lp[n]] * (lp[n] - 1)

    These are exactly the two cases in savinov's if-else statement in the code above.

    Sorry for the bad editing. This is my first comment.

    → Ответить
  • »
    »
    11 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Using the fact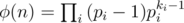 you can obtain it by simple calculations. Try to understand when we take into account some prime at first time.

    → Ответить
»
11 лет назад, # |
← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится 
#include<cstring>
#include<iostream>
#include<ctime>
using namespace std;
#define N 100000005

bool vis[N];
int p[N], cnt, phi[N];

int Euler(int n){
	int i, j, k;
	phi[1] = 1;
	for (i = 2; i < n; ++i){
		if (!vis[i]){
			p[cnt++] = i;
			phi[i] = i &mdash; 1;
		}
		for (j = 0; j < cnt && i * p[j] < n; ++j){
			vis[i * p[j]] = true;
			if (i % p[j]) phi[i * p[j]] = phi[i] * phi[p[j]];
			else {
				phi[i * p[j]] = phi[i] * p[j];
				break;
			}
		}
	}
	return cnt;
}//O(n)
→ Ответить