Блог пользователя saba_tavdgiridze

Not programming problem at all.
Автор saba_tavdgiridze, 11 лет назад, По-английски

N numbers : a_1 ,a_2 ,a_3 ... a_N are written like this a_1 / a_2 /a_3/ .../a_N (there /-means division).You Can add some brackets .For example if sequence is : 5/6/7 you can make it like : 5/(6/7) .Your task is to maximize this product.Like example below it is 5/(6/7).Any algorithms?Thanks in advance!

  • Проголосовать: нравится
  • +11
  • Проголосовать: не нравится

»
11 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

I think you can try to search information about Catalan Number

→ Ответить
  • »
    »
    11 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    If i try all balanced bracket sequences it will be brute force,and Catalan formula is :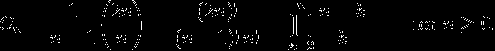 and it is very big number,for example for N=1000 and I think it never stops.

    → Ответить
»
11 лет назад, # |
  Проголосовать: нравится +3 Проголосовать: не нравится

The first thing that comes to my mind is this naive O(n^3) dynamic programming solution:

For every i,j (1<=i<=j<=N) find the largest and the smallest possible result you can get when sequence Ai/Ai+1/Ai+2/.../Ai+n is written and brackets are added. You can do this with dynamic programming: If i=j, the smallest and the largest possible result is Ai. For i<j, and for every k, i<=k<j, consider the following placement of brackets: (Ai/Ai+1/Ai+2/.../Ak)/(Ak+1/Ak+2/.../Aj). This expression will have the smallest possible value when Ai/Ai+1/Ai+2/.../Ak has the smallest possible value and when Ak+1/Ak+2/.../Aj has the largest. When you want to find the largest value it's the other way around. So, for every i<j you just try all possible k. You should have a basic concept of what dynamic programming is. There's probably a faster solution though.

→ Ответить
»
11 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Are the numbers in your array all positive and greater or equal to 1?

→ Ответить
  • »
    »
    11 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    All numbers are integers.

    → Ответить
    • »
      »
      »
      11 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      So, negative numbers are allowed?

      → Ответить
      • »
        »
        »
        »
        11 лет назад, # ^ |
          Проголосовать: нравится +5 Проголосовать: не нравится

        It doesn't mattar.

        If there's odd number of negative signs then the answer is always negative regardless of how you put the brackets , in this case you should minimize the absolute value of the answer.

        If there's even number of negatives then the answer is always positive in this case you should maximize the absolut value of the answer

        → Ответить
»
11 лет назад, # |
  Проголосовать: нравится -8 Проголосовать: не нравится

h(n)(Catalan Number) is the number of different ways n + 1 factors can be completely parenthesized (or the number of ways of associating n applications of a binary operator). For n = 3, for example, we have the following five different parenthesizations of four factors: ((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd)) When the number is too big ,you can use the formula:h(n)=C(2n,n)/(n+1),and you may use Bignumber

→ Ответить
  • »
    »
    11 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Yes, but the original question does not ask how many ways there are to parenthesize. It asks the maximal result possible with some particular parenthesization, an entirely different problem. If you are suggesting a bruteforce, as mentioned earlier, it will take forever even for small numbers.

    → Ответить
»
11 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

The best thing I came up with is this (assuming I understood your problem well):

If the first number in the array is zero, the result is zero. If there is a zero elsewhere, the result is undefined (as division by zero cannot be avoided).

Now we assume that the array is zero-free. If there is an odd number of negative numbers, the result will surely be negative. To maximize it, we simply don't place any brackets. If there is an even number (incl. 0) of negative numbers, the best way to put brackets is: a_1/(a_2/a_3/a_4/.../a_n)

(all this assuming the numbers are integers)

→ Ответить
  • »
    »
    11 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    yes,i think you understand this problem.I think like you,but it needs proof.

    → Ответить
    • »
      »
      »
      11 лет назад, # ^ |
        Проголосовать: нравится +3 Проголосовать: не нравится

      Proof:

      Assume that all numbers are positive and we wish to maximize the expression. Every number in the sequence A[1],A[2],A[3],... will, in the end, be raised to an exponent of either 1 or -1. Since A[i] is a positive integer, A[i]^1>=A[i]^-1. So, we want to have the largest possible number of 1-exponents and to somehow minimize the number of -1 exponents. Observe A[1] will always have the 1-exponent and that A[2] will always have the -1 exponent. In the configuration A[1]/(A[2]/A[3]/A[4]/.../A[n]) all the other numbers have 1-exponents, and thus that configuration is optimal.

      Assume now that all the numbers are positive and we wish to minimize the expression. Now we want to minimize the number of 1-exponents. The obvious way to do this is simply not using any brackets.

      If there are negative numbers just observe the parity of their total count, as I explained earlier.

      → Ответить