Or_ion's blog

Solution to this problem
By Or_ion, 2 years ago, In English

Given an array of size N, you have to answer several query on the given array

query have the following format

query will consist of two positive integers L and R such that 1<=L<=R<=N denoting a subsegment of array from L to R

For a given query you have to calculate

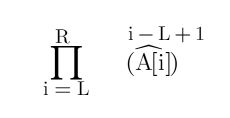
if answer is too large print modulo 1e9+7

1<=N<=400000 and 1<=Q<=400000

Where N is the length of array and Q denotes the number of queries.

Sample

4 1

1 2 3 4

2 4

2*(3)^2*(4)^3 == 2*9*64 = 1152

i cannot think of solution for this problem can anyone help me?

  • Vote: I like it
  • -4
  • Vote: I do not like it

Comments Comments (5)
| Write comment?
»
2 years ago, # |
← Rev. 7   Vote: I like it +16 Vote: I do not like it

use two prefix arrays:

pre1[] and pre2[].
where 
pre1[1] = a1;
pre1[i] = pre1[i-1] *  pow(ai,i); (i>1)

pre2[1] = a1;
pre2[i] = pre2[i-1]*ai; (i>1)

The answer now is : ( pre1[R] / pre1[L-1] ) / ( pow(pre2[R] / pre2[L-1], L-1 ) ) when L!=1  else no need to divide.
If modular arithmetic is involved use modulo inverse instead of division.
→ Reply
»
2 years ago, # |
← Rev. 7   Vote: I like it 0 Vote: I do not like it
Idea

Let me know if I have missed something. (*^▽^*)

UPD: I didn't mention modulo multiplication and division anywhere but I think you can make necessary changes yourself.

→ Reply
  • »
    »
    2 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I mentioned the same thing but I don't think its wrong.

    → Reply
    • »
      »
      »
      2 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      The answer now is : ( pre1[R] - pre1[L-1] ) / ( pow(pre2[R] - pre2[L-1], L-1 )

      This doesn't look correct. Why are you subtracting?

      → Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

nice problem

→ Reply