Given, two disjoint sets with roots 1 and 6 respectively which already have their childrens' paths compressed.
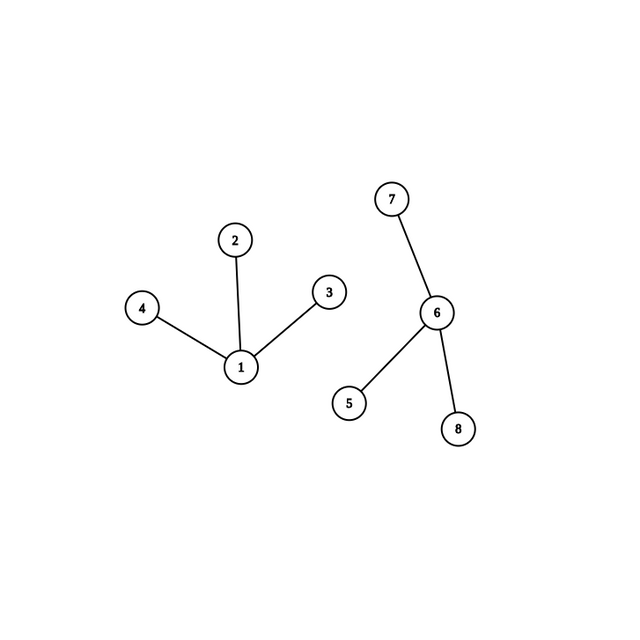
I wish to do a union but instead of
this
I want
this
Unable to figure out a way to do this optimally.
DSU I am using is on cp-algorithms
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Given, two disjoint sets with roots 1 and 6 respectively which already have their childrens' paths compressed.

I wish to do a union but instead of
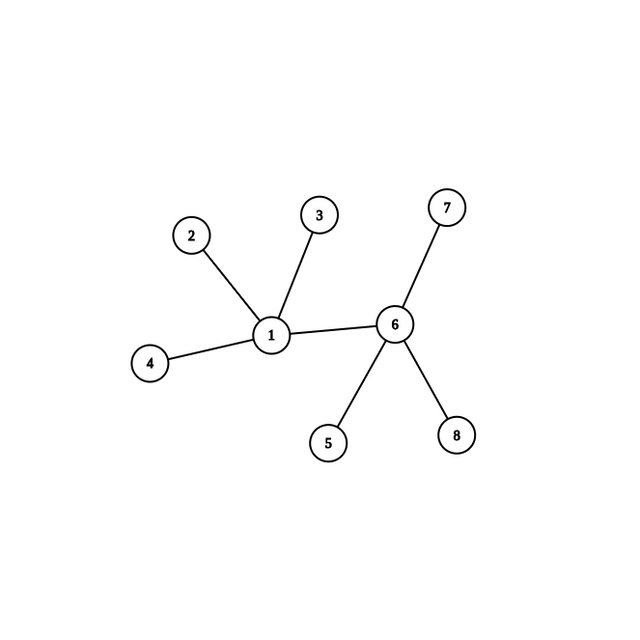
I want
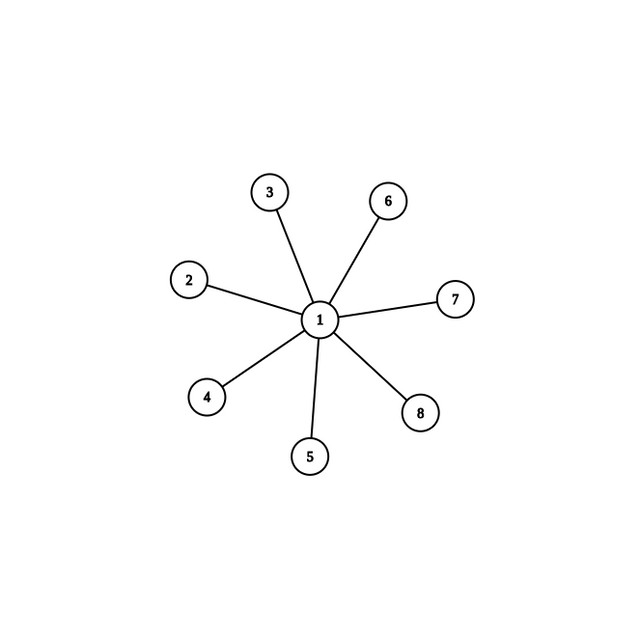
Unable to figure out a way to do this optimally.
DSU I am using is on cp-algorithms
| Name |
|---|



On the cp-algorithms page there is an example of this under the title "Storing the DSU explicitly in a set list".
It will also return the first form and it still requires me to run a recursive
find_setonce to achieve the second form from the first, which will give meO(n^2)in the worst case. I guess there is no way, I should probably give it up for now. Thanks for your comment.Why should it? Let's do the following.
We maintain the invariant that after any merge operation, every single component is a star graph (I hope that is what you meant).
Let's maintain the sizes of every component in a array called sz, and for each "representative", a vector of all the vertexes that belong to him (let it be g). Now, we use the small-to-large technique — when we merge components with representative P_a and representative P_b, (|P_a| > |P_b|), we simply iterate over all vertexes in g[P_b], add them to g[P_a], increase the size of P_a by |P_b|, and directly link them, thus maintaining the invariant. As every time a vertex gets redirected, the size increases at least two times, each vertex will be merged no more than O(NlogN) times, and we get a runtime ofO(NlogN + Q)
I'm not sure what you mean, you can directly create the graph you wanted from the lst array?
The first picture would have two non-empty entries in lst:
You then merge any node in lst[1] with any node in lst[6] and you'll end up with one item in the list:
Every node will also have parent[x] = 1.
It looks like the worst case complexity is bad but small to large merging ensures that it isn't O(n^2) as each item would only be moved at most log n times.
Thank you induk_v_tsiane and robostac for the explanation. I didn't notice the fact that each item doesn't get moved more than
log(n)times.I think you mean this:
You can check how this code works in EDU : DSU, pretty useful. Hope i helped