Note that this weekend (Friday 7.3. to Monday 10.3. inclusive, ± time zone), this year's last round of USACO (before US Open) takes place.
You'll be able to access the contest from the USACO page. Registration is required.
Feel free to discuss the problems here after the contest ends (which is, btw, not very clear, because there are no official start/end times posted — around Tuesday afternoon in UTC). I'll probably also post my solutions here.
Also notice how similar this is to my blog post about COCI :D. This is one of the usual Crazy Weekends — there's COCI, USACO and start of the Codechef Long Challenge. It's like the contest organizers do this on purpose...
UPD: The results are up now!
UPD: Negative votes... trolls growing strong here!
UPD^2: Trolls are gone now. Lol.
**UPD **
Solutions (gold)
The Lazy Cow (code)
We're given N points (xi, yi) in a plane, each with a weight gi and are supposed to find a point (x, y) which maximizes the sum of gi of points located at a distance of at most K from (x, y). The distances are Manhattan ones — the distance of point (xi, yi) from our (x, y) is |xi - x| + |yi - y|. Constraints: N ≤ 105, coordinates 0 ≤ xi, yi ≤ 106, 1 ≤ K ≤ 2·106.
Let's say that we picked a point (x, y). We can transform coordinates (x, y) to (x', y') = (x + y, x - y) and similarly for all points i. In these new coordinates, the distance of our point from any given one is (evaluating all possibilities for what the abs. values can look like) 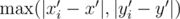 , and the region for which it's ≤ K is a rectangle around (x', y').
, and the region for which it's ≤ K is a rectangle around (x', y').
Let's sort the given points by x'-coordinate. Now, we can use a sweepline + interval tree, which supports operations "add value v to all elements of interval I" and "get maximum of all elements". We'll try adding the points one by one, in the order of increasing x'-coordinate, and in the interval tree, we'll remember the sum of gi of points that we could get by picking y' as the other coordinate in the element y'. That's done by adding gi to all elements from yi' - K to yi' + K inclusive; removing a point is the same, just with subtracting gi from all those elements.
We need to remove the points whose xi'-coordinates are < x' - 2K (we're basically forcing the right side of our rectangle to touch some point and store in the interval tree only answers when accounting for points that have the xi'-coordinate ≥ x' - 2K; if it didn't, we can move the rectangle to the left without changing the result). Since the points are already sorted, we can use two pointers... well, just one additional "pointer", which points to the leftmost point still in the interval tree.
The time complexity of constructing an interval tree is O(maxX); each query can be processed in 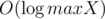 time and the sorting takes
time and the sorting takes  time, so the resulting complexity is
time, so the resulting complexity is 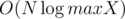 . With y'-coordinate compression, we can get
. With y'-coordinate compression, we can get  runtime.
runtime.
Sabotage (code)
We're given an array A of size N ≤ 105, and are asked to compute the minimum arithmetic average of all elements of this array after removing a substring (contiguous subsequence) from it. Plus some additional constraint that the elements of this array are non-negative, at most 104 and we can't remove the first or last element from A.
This type of problems (serarching for some arithmetic average) can usually be solved with bin-search. It's clear that if we can achieve an average of at most x, then we can achieve also at most y > x. So let's fix x and check if we can achieve ≤ x.
Prefix sums are useful. Let S[i] denote the sum of the first i elements (S[0] = 0). Let's say that we erased the subarray A[i..j] (2 ≤ i ≤ j ≤ N - 1) and got an average ≤ x. It means that
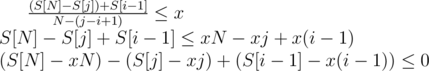
Let's say that we fixed j. Now, the best choice (minimizing the left side of this inequality) is obviously picking the smallest S[i - 1] - x(i - 1). This gives us a simple way of checking if this inequality ever holds: iterate over j from 2 to N - 1, remember and update the minimum of all S[i - 1] - x(i - 1) (always just picking the minimum of smallest the one found so far and S[j - 1] - x(j - 1)) and check if the smallest value for given j is ≤ 0. If it never is for given x, there's no way to get an average ≤ x.
This check works in O(N) time; plus binsearch, it's  time.
time.
Counting friends (code)
We're given an array of N + 1 elements (N ≤ 500) and are supposed to find, and list in sorted order, all possible elements of this array such that after removing said element, the remaining ones can be degrees of a simple undirected graph.
Why not try to remove each element and check if the remaining ones are degrees of a graph? We have a simple way of checking whether they are: the Erdős–Gallai theorem, which provides a necessary and sufficient condition.
Let's sort the numbers beforehand. Now, we can get a sorted array after removing an element in O(N) time without much difficulty. For each removed element, we can just compute the sums on both sides of the inequality from Erdős–Gallai theorem for all k (possibly with some optimizations), which gives us an O(N3) time complexity.











When will the registration link be put up? Currently there seems to be none.
Registration to the usaco.org is required, but not for contest.
I didn't realize it could be misunderstood like that. This is not like CF contests, with separate registration running for each contest :D
You just need an account on the USACO site to compete, and register for that account.
This weekend seems to be more crazy because of the 8th of March :)
Does anyone know the exact time when the contest will begin? I'm at GMT -3 and in the USACO page there's no info.
It'd be nice if someone could post a link to www.timeanddate.com so that we all can see the time converted to our time zones.
the contest began, link
Nice problems. I am waiting for your solutions. :D
My first Gold Contest! I'm very excited!
USACO should add a division above Gold. Like, Platinum or something. With all seriously hard problems.
Are you getting perfect score for a tenth time in a row?
I haven't had a decent challenge for the... fifth time in a row, maybe? By decent challenge, I mean at most one quickly solvable problem — so far, it's around 2.6 quickly solvable ones on average.
I don't get perfect scores because of Null feedback and my laziness to write a bruteforce and test a problem that might have a silly bug, if there's hardly anything to gain.
And the level of Gold division in USACO is often the level of Div1 in CF.
I miss the good old times where problems were really challenging in the sense that it revealed a new technique, a new data structure, a new algorithm, a new way of thinking, I remember the convex hull optimization, segment trees, bitmasks DPs, the ultra-hard flow problems and the WTF greedys. Now there are a just a few original problems. Anyway, for me, it continues to be quite challenging.
The US Open next month should have harder problems, since it's their flagship contest (and major consideration in who to invite to camp). But keep in mind that a big purpose of USACO is to help determine the US IOI team, so really hard and novel problems that don't help in IOI preparation will be rarely found in USACO.
Of course, USACO is still hard for me! I hope someday to be able to complain about how easy Gold division is :-D
The link in the post of the time when contest ends is wrong.It should end on March 11,16.00UTC,not March 10.The USACO website says the deadline to start contest is "Mar 10 at 23:59 UTC-12 time",which is Mar 11,11.59UTC.
Right. My mistake.
I've finished my first Gold contest. Problems are exciting, and I can't wait the result :-)
Finished Bronze. Hope I can be promoted to Silver.
Thanks Xellos for sharing ending time of the contest. :)
This is my first USACO Contest this season, and I really enjoyed it. The problems were very interesting.
And, I don't know about other contestants, but I found them challenging. One of them had me thinking for over two hours...
I'll post my solution in a couple of hours when the contest ends.
Contest has ended!
Can someone tell the problems from his/her division. And how to solve(in spoiler).
According to Xellos's Time announcer, it hasn't ended yet.
Besides, you can find all problems with solutions from all divisions after it finishes. They'll be published with the results.
The problem is just how fast they'd be published. It's been fine this year, but it used to last weeks before.
It hasn't ended yet. Registration closes at 12:00 UTC, but people who start the contest just before that will be coding until 16:00 UTC (40 minutes from the time of this post).
Now It has been ended! Hope result will be come until the next month!!!!
Contest has ended. I'll share my solutions.
1) The Lazy Cow
The area from which the cow can reach a certain point (x, y) is determined by the rectangle with vertices (x - K, y), (x + K, y), (x, Y - K) and (x, y + K). That rectangle's sides form 45º angles with the grid lines. So we can rotate the plane 45º counter-clockwise and scale its size by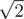 , so that if (x', y') are the coordinates in the rotated plane of the old point (x, y), then x' = x + y and y' = y - x. Now the rectangles will be parallel with both axis and we can do a sweep line algorithm in one axis while maintaining a segment tree with the grass available on the other one.
, so that if (x', y') are the coordinates in the rotated plane of the old point (x, y), then x' = x + y and y' = y - x. Now the rectangles will be parallel with both axis and we can do a sweep line algorithm in one axis while maintaining a segment tree with the grass available on the other one.
To do the plane sweep, for a certain patch of grass located at (x', y') that has g units of grass, add an event (y' - K, y' + K, g) at x coordinate x' - K, and an event (y' - K, y' + K, - g) at x coordinate x' + K + 1. The events should be sorted by increasing x coordinate and delete events before add events in case of a tie. Watch out for large coordinates too, you'll never need anything lower than 0 or bigger than 2000000.
Running time: O(N log M) (where M = 2000000 (the range that y coordinates can take in the plane sweep)
C++ Code
2) Sabotage
This one had me scratching my head for over two hours...
What if we could determine if a certain average k can be obtained by correctly choosing which block to remove? If there was an efficient way to do that, we could simply binary search on the value of k (30 iterations would be more than enough to ensure 10 - 3 precision).
To determine if we can obtain an average ≤ k, we'd have to find two blocks of machines, one starting from the left and one starting from the right, such that the average of all of them is ≤ k. The problem here is that the amount of machines we choose alter the average. The trick to overcome that obstacle is to notice that if we modify all elements of array M, so that Mi = Mi - k, we'll have to find two blocks of machines such that their average is ≤ 0. But that's the same as saying that their sum is ≤ 0, and that doesn't depend on the number of elements!
So what we do is modify the array as said in the previous paragraph, and then do a precalculation lefti, which keeps the prefix sum of all machines from 1 to i inclusive, and righti, which keeps the suffix sums of all machines from i to N. After that iterate on the left block of machines, starting from N - 2 and going down to 1, and at each step, check if the the current prefix sum (lefti) + the minimum suffix sum so far on the right (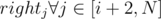 ) is ≤ 0. If it is, then you know you can do it.
) is ≤ 0. If it is, then you know you can do it.
Running time: O(N log M)
C++ Code
3) Counting Friends
This problem asks us to build a graph from a list of degrees of its nodes. The fastest way I know to determine if it's possible is Erdos-Gallai's theorem (consult here for more info on the theorem). Then simply remove one element at a time and check if the residual list of elements is a graphic sequence using Erdos-Gallai. If it is, add the element you removed to a list. Finally, just output that list.
Running time: O(N3)
C++ Code
Is O(N3) fast enough for Counting Friends? I thought that would be too slow, so tried out a linear-time variant of Erdos-Gallai over each removal, for O(N2) time overall.
No point going into the exact optimisation, since it seems to have been "discovered" plenty of times already: https://www.google.co.uk/search?nfpr=1&q=erdos+gallai+linear+time
C++ (probably broken, as always)
It is fast enough. 5003 = 108 and if we compute the left side sum from the one found in the last step, it's halved. The constant factor is incredibly low.
Sounds believable -- although a bit disappointing, because to me the O(N3) solution is trivial with the most interesting part being getting it to run faster.
As others have said: maybe it's wrong to expect really hard problems from a school-level competition (at least, outside Eastern Europe :).
I'm unlikely to get 100% points for this anyway, due to the evil N+1=501 case...
Hey, in Counting Friends I have used the following heuristic approach for checking if d1,d2...dn are degrees of a graph's vertices :
Sort the numbers d_i
Draw edges from vertex of degree d_n-1 to vertices n-2, n-3...
Remove vertex n-1 from the graph and do the following again.
It's probably wrong, though i was not able to come up with an counterexample — could any of you suggest one or prove that it is correct?
Yes, it's correct. See the "Degree sequence" Wiki page for a proof and some references:
http://en.wikipedia.org/w/index.php?title=Degree_(graph_theory)&oldid=589217949#Degree_sequence
It should be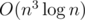 though with a "naive" implementation, which could be too slow. How did you implement the decrementing and reordering?
though with a "naive" implementation, which could be too slow. How did you implement the decrementing and reordering?
After decrementing the sorted list of degrees, there are now two sorted runs. It is possible to merge these in O(n) time using the same merge as mergesort, so we have an O(n3) algorithm.
My implementation is here: https://www.dropbox.com/s/kch5oalet0ogql7/fcount.cpp
@below: Sorry, fixed. :)
Right, good observation :)
I guess you meant merge sort there instead of quick sort ;)
They say that contest is still running :"Contest is Running!". How can you explain this:D? Thanks
I wouldn't be surprised if it says "Contest is running" until they publish the results. Instant updates aren't really USACO's strength.
Aa ok, i understand. When will our result be published?
We can just hope that it comes soon. That is, in a week.
There is no my name in results, but i have solved problems. What does it mean? And what i must to do to see my results?
In what results? AFAIK there should be no results for this contest yet, you have nowhere to see your name in.
I'm stupid. I saw at the last year results. I'm forget that now is 2014, not 2013)
I wrote on second problem ternary search for searching length of cutting segment. When it is not correct?
When the cost function is not unimodal.
I would like to add my contribution even though the solutions that were written here are undoubtly better. I won't explain my solution for the first problem as it turned out to be completely wrong.
2) Sabotage: binary search of the answer. I use a cumulative array sum and a
std::dequeto keep the minimum on a sliding window. Code.3) Counting friends: Erdös-Gallai theorem. However I didn't think an O(n3) solution would be sufficient so I used a bit of precomputation to implement it as O(n2). Code.
You may have noticed silly bugs in my algorithms or implementations. As you can see I am far from being an expert.
I tested your code for sabotage exhaustively and it gives the correct answer 99% of the times. The only case I found where it fails is, for example, in the following input...
3 5 1 6
Your program fails to consider that Farmer Paul will always disconnect at least one machine, so it outputs 4.000, when actually the correct answer is 5.500.
That's also a pretty stupid restriction. Instead of putting clarifications like this only on the main site, they should have updated the problem statements.
Thanks, indeed my solution doesn't handle this corner case.
In fact when I did the contest (Saturday), there was no such clarification! It has been added afterwards.
Yes, it's really stupid.
And in case that it was added afterwards, there should be no test case where the answer involves that. It's unfair for those contestants who took part earlier.
Heck, even if it had been added right at the start of the contest, it's still very unfair, because most contestants don't read the silly things that are written in the main page, like the rules or the objectives. They should have updated the problem statements, just like niklasb said.
Finally there were two tests where the best solution was to disconnect no machine. 619 in overall as for me (congrats to diego_v1 and Xellos who scored 1000).
I made a generator for Counting Friends, and I tested your code too. It gives the same answer as mine and Xellos's everytime, which I think should be correct.
Could someone please suggest a good tutorial for Interval tree + sweep line algorithms? Xellos, Could you please explain how the (x1,y1)=(x+y,x-y) thing works. I'm not very good with geometry problems. This looks like a very helpful trick. :)
Plus, if you can, please mention the sort of problems that can be made easy with this trick. Thanks again.
I wrote about it in this comment.
I used a segment tree instead of an interval tree, but I did use a sweep line approach. Here's an understandable tutorial -> LINK
And about the thing that (x', y') = (x + y, y - x) is because I rotated the plane 45 degrees so that the rectangle that determines the area from which the cow can reach the spot (x,y) becomes parallel to the x and y axis, hence making a sweep line algorithm possible.
As a side note, you can also use a diagonal sweep line for this problem, but I feel more comfortable with rotation + standard sweep line.
In English literature, it's called a segment tree, but I call it an interval tree because (as a transliteration from Slovak), because it supports operations on intervals. Not on line segments.
Ahhh, so you did use a segment tree after all!
I thought you had used this -> Interval Tree
This come from 8 queens approach.
Here if you need geometrical explanation:
Clockwise rotating alpha° around origin (0, 0):
newx = cos(alpha) * x + sin(alpha) * y
newy = sin(alpha) * x — cos(alpha) * y
If we rotate all points to 45° CW, we have cos(alpha) = sin (alpha) = 1 / sqrt(2) Scale all point coordinates by factor *sqrt(2), we have:
newx = x + y
newy = x — y
Is the problem solvable similarly if the distances are euclidean?
If the distances were euclidean, the areas reachable from a certain point would be defined by a circle of radius K instead of a rectangle. I don't think you can use a plane sweep to solve that, but I'm a novice at geometry, so maybe I'm wrong.
The problem becomes a lot trickier when the distances become euclidean, as you have to deal with squaring and such. This post gives quite a bit of information regarding the problem: http://www.quora.com/Algorithms/What-is-an-algorithm-for-enclosing-the-maximum-number-of-points-in-a-2-D-plane-with-a-fixed-radius-circle
Interesting. So that version of the problem can't be solved nearly as fast...
Yeah, it could give some insight, but it's actually the inverse problem: Given a collection of points, enclose as many of them as possible with a fixed radius circle. In this case, the problem would be: Given a collection of circles of a fixed radius on the plane, find the point that is inside the maximum number of circles.
It's actually the same problem
I was thinking of circles of radius K around the patches of grass. Then you would need to find a point that is inside the maximum number of circles...
But actually, you're right, if you think of it the other way around, it's the same problem. If the circle is around the position of the cow and the points are the patches of grass, then you have to cover the maximum number of points with the circle of radius K.
Counting Friends: Firstly, talking about O(n^3) solution To check a list of vertex degrees is correct or not. We sort the list of vertices in order of increasing of degrees: d[1] <= d[2] <= ... <= d[n], and for each d[i] from d[n] to d[1], we select d[i] vertices before vertices i in the list, and then decrease their degree by 1, if any vertex having negative degree, the checking process fail, otherwise, the degrees are correct. Checking take O(n^2) time, therefore the algorithm take O(n^3) time complexity. Secondly, to improve the performance, we can apply a trick to maintain the list d[1], d[2], ..., d[n] always in increasing order. Decreasing a range of d[...] by 1 can be implement efficiently using Fenwick trees, finding the range of d[i] vertices at each step using binary search (indirectly using a Fenwick tree) take O(log^2(n)), so totally we have O(n^2 log^2(n)) solution
If you use a Fenwick Tree, how do you maintain the list sorted at all times? Suppose the following example...
2 2 2 2 2 4
After one iteration, it will look like this...
2 1 1 1 1 0
EDIT: Yeah, I get it now. Assuming array D is sorted in non-increasing order. Suppose you process element Dk = x and decrease by 1 all elements in the range [k + 1, k + x], then you do a binary search in range [x + 1, N] to find the last elements i such that Di = D(k + x) + 1. Let s = min(i - (k + x), Dk), then you add 1 to every element in the range [k + 1, k + s] and subract 1 to every element in the range [i - s + 1, i]. I may have miscalculated somewhere, but I get the idea.
Complexity Analysis: Anyway, this would take N * log(N) operations for the initial sort + log(N) everytime you process an element + log2(N) for the binary search + 2 * log(N) to re-sort the array, which makes a total of 4 * N * log(N) + N * log2(N). For the case that N = 500, this gives approximately 58500 operations for every run of the algorithm, and there are N runs in total, which means there would be around 30 million operations, which, in theory, would be 400% faster than the normal O(N3) algorithm. But the constant factor in this approach is much higher, so I doubt there's THAT much speed gain. I'd need to test it.
If, on the other hand, we were to use a Fenwick Tree for the Erdos-Gallai approach, then that would REALLY be fast.
@diego_v1: You're right, although I got full score for this problem, there is another better implementation using this approach, it take O(n^2*log(n) time as in author's note.
And I notice that you have full score also.
results
official code for "lazy" problem in silver gives 12 for the following test while I believe it should be 9
You should email bcdean@clemson.edu so that he can re-evaluate the submitted solutions.
Is there a way to get the code I sent during the contest?
I have awful results for Irrigation and Mooomoo and I have no idea what's wrong, because my theoretical solutions are the same as the official ones.
UPD: Oh, I found it.
"The Gold division had 0 total participants, of whom 50 were pre-college students." :D
yeah I also noticed that they mention that 13 participiants submitted at least one solution in my country SYR while I can see only 10 in total in results pages of the three divisions. and this is not the only month that they mention this number wrong