Задача: Найти сумму всех комбинаций перемножения натурального ряда от 1 до N

На данную задачу есть решение на GeeksForGeeks работающее за O(n^2).

В данном посте я представлю решение в виде формулы выведенной методом индукции.

Решение

ВАЖНО: Заметим что ответ на задачу не меняется, если начинаем мы с 0. Поскольку все комбинации включающие 0, просто на сумме не отразятся.

База индукции

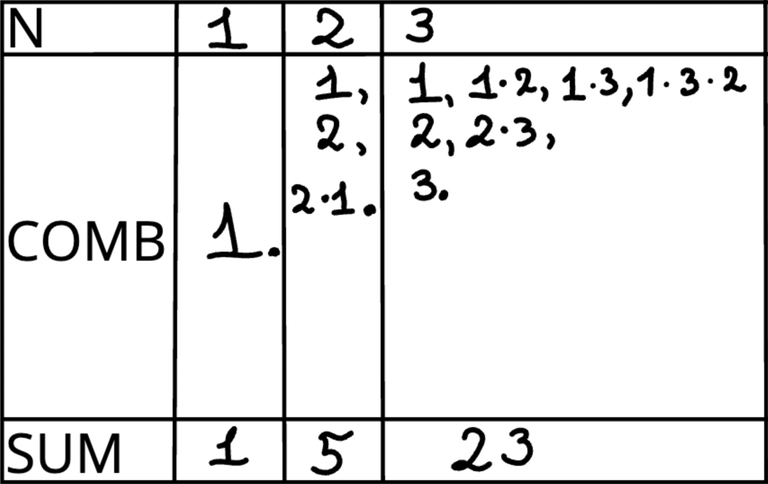
Здесь я просто рассматриваю случаи на маленьких n и пытаюсь найти закономерность.

Доказательство для N

• n! - 1 Это сумма произведений входящих до n — 1. (зеленная рамка)
• n * (n!-1) Формула, которая образуется если во все предыдущие комбинации добавить наше n. В таком случае мы получим новые комбинации, которые не встречались ранее. (красная рамка)
• n Это оставшееся единичное подмножество из самого n. (синяя рамка)

В итоге просуммировав эти комбинации мы получим: (n!-1) + n * (n!-1) + n

Сократим вышеприведенную запись. Конечная формула: (n + 1)! - 1

Очевидно что итоговый ответ в виде кода будет работать за O(n). Понятно, что при больших N наш факториал будет замедляться. Но это точно лучше, чем обходить комбинации за квадрат.