jerseyguy's blog

Help (graph problem).
By jerseyguy, history, 2 years ago, In English

question :

Given n cities and m roads b/w them. Each road is represented as [L,R,X] L is the starting city, R — the ending city, and X the cost.
Also for all roads L<R . If there is a road from city L to R with cost X then one can travel b/w any two cities that lie b/w L and R(inclusive) with cost X.

Find the minimum cost to travel from 1 to N.

T<=10
N,M <= 1e5
L,R<=N
X<=1e6

My approach : sorting and priority queue , but it gave WA

sample:
2
4 1
1 3 10
4 3
1 4 10
1 2 5
2 4 3

op:
-1
8

  • Vote: I like it
  • +1
  • Vote: I do not like it

Comments Comments (2)
| Write comment?
»
2 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Well, you only need forward edges.

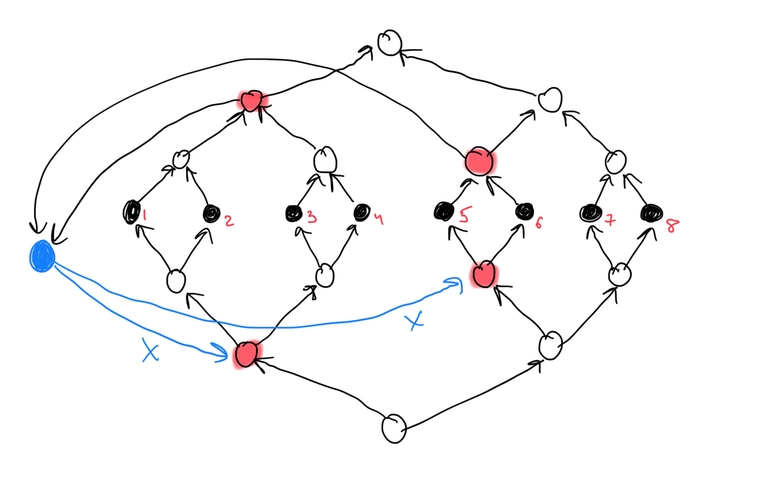
You can try to use a segment tree to store minCost of getting to point x, then when you want to move along just get the minimum cost on the current segment and update the range of the segment. The segments should be sorted increasing by L. Correct me if I am wrong, but time complexity should be O(MlogM+(N+M)logN) from sorting and segment tree.

→ Reply
»
2 years ago, # |
  Vote: I like it +6 Vote: I do not like it

You can view the cities as an array of nodes, on top of which we can construct a segment tree. The segment tree in this case will be a part of the directed graph. We will construct two versions of the segment tree: one in which the edges point towards the node's parent (tree 1), and one in which they point towards the children (tree 2). All of these edges will have weight 0.

Now, when we add a road, we want to decompose the segment [L, R] into multiple nodes in the segment tree. Number of these segments is $$$O(log n)$$$.

We have to connect each node from tree 1 to the nodes' copies in tree 2 by edges of weight X. This way, when we're standing at position $$$pos$$$, we can go to one of the segments covering $$$pos$$$ in tree 1, move to tree 2 with cost X, and descend to any other position in [L, R] that we need.

However, connecting each pair of nodes would cause $$$O(log^2 n)$$$ edges to be added per query. To improve that, we can instead introduce a fictive node, connect all nodes from tree 1 to it by free edges, and connect the fictive node to the needed nodes in tree 2 by edges of weight X. This way, the number of edges per query reduces to $$$O(log n)$$$.

Now, we simply run Dijkstra on this graph. Number of nodes is linear, but number of edges is $$$O(M*log n)$$$. Hence, total complexity is $$$O(M*log^2 n)$$$.

For clarification, see the image. It shows the structure of the trees for n=8 and the way you would process the query [1, 6, X]. All black edges have weight 0, and blue ones have weight X.

→ Reply