FunnyScientist's blog

Sum of GCD of all contiguous subsequence
By FunnyScientist, 11 years ago, In English

I'm learning number theory and I cannot figure out the solution of following problem:

Given an array of integer A with N element with constrains N <= 10^5, A[i] <= 10^12. We call GCD(L, R) is greatest common divisor of all element A[L], A[L + 1], ..., A[R]. Return the sum of all contiguous sub-sequence in A.

I did have some idea that, for fixed index i, the value of GCD(i, j) will be decreasing as GCD(i, j) >= GCD(i, j + 1). Also, because GCD(i, j + 1) must be equal or divisor of GCD(i, j), the number of distinct value X of GCD(i, j), GCD(i, j + 1), ..., GCD(i, N) will satisfies 2^X <= A[i].

But I cannot go further. Please give me some more insights.

  • Vote: I like it
  • +8
  • Vote: I do not like it

Comments Comments (15)
| Write comment?
»
11 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

Yes, for every i GCD decreases at most lg(A[i]) times. If you could calculate GCD(i,r) for any fixed r fast enough, then you could find all the positions where GCD changes using binary search.

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    Thank you very much. Value GCD(i,r) can be computed by using Segment Tree in Log2(N), but I found that for N = 1e5 and large A[i] it somehow still slow. Is there any more efficient method for query operation? Currently it looks like that:

    ll query(int node, int l, int r, int i, int j)
{
	if(r < i || j < l)
		return -1;
	if(i <= l && r <= j)
		return it[node];
	ll p1 = query(Lc, i, j);
	ll p2 = query(Rc, i, j);
	if(p1 == -1) return p2;
	if(p2 == -1) return p1;
	return gcd(p1, p2);
}
    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it -8 Vote: I do not like it

      You can use RMQ, but instead of min/max use gcd. Queries can be answered with only one gcd call. Make sure to use a fast gcd implementation.

      → Reply
    • »
      »
      »
      11 years ago, # ^ |
      ← Rev. 2   Vote: I like it +10 Vote: I do not like it

      you can compute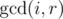 in 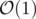using Sparse Table data structure (instead of Segment Tree).

      → Reply
»
5 years ago, # |
← Rev. 3   Vote: I like it -25 Vote: I do not like it

I came across a similar question recently in which I have to find the sum of GCD's of all subarrays.

I know that GCD decreases at most log(A[i]) times so I can find all the positions where GCD decrease using Binary Search and sparse table but I am unable to think that how should I find the sum of GCD's of all subarrays from range L to R.

My approach is O(nlogn) for a single query, can it be done faster and more efficiently if there are multiple queries?

ex- A = [2,3,4,5]

L = 1, R = 4 (1-indexed)

ans = 20.

→ Reply
»
5 years ago, # |
← Rev. 2   Vote: I like it +2 Vote: I do not like it

Yeah ! my idea is mostly the same as discussed above. And here my code goes -->

https://ide.codingblocks.com/s/135466

Although i have added comments to make my code readable.

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you please share the problem source?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Will you explain me the solution of above problem?

    → Reply
    • »
      »
      »
      9 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Sorry for late reply,

      We don't need any complicated data structure to solve this problem

      The only observation we need is that the number of distinct gcd values ending

      at a given index is atmost log(n), so we can maintain a map that tells us all

      the distinct gcds that have ended in the previous index, using this we calculate

      all the new gcds and also update the map simultaneously

      Submission link:https://mirror.codeforces.com/contest/475/submission/250578491

      Also please share any different approach that you may have learnt of during this time

      → Reply