Thanks for your participation! I am so sorry for my careless review. We were preparing for this round for many months and made some problems which writers and testers are all like. We do want to give everyone a good time to enjoy the contest. But carelessness is deadly. In problem B, some test cases should have been made, but we missed them in not only the pretests but also the final tests. In fact, we had not noticed it until some suspicious hacks appeared. I and all co-authors sincerely regret our mistake and hope you can forgive us.
Besides, few people are cyberbullying authors, please do not do so. If you have a bad experience, you can downvote me because of our fault.
1774A - Add Plus Minus Sign
Idea: Cirno_9baka
The answer is the number of $$$1$$$s modulo $$$2$$$.
We can get that by adding '-' before the $$$\text{2nd}, \text{4th}, \cdots, 2k\text{-th}$$$ $$$1$$$, and '+' before the $$$\text{3rd}, \text{5th}, \cdots, 2k+1\text{-th}$$$ $$$1$$$.
#include <bits/stdc++.h>
using namespace std;
char c[1005];
int main() {
int t;
scanf("%d", &t);
int n;
while (t--) {
scanf("%d", &n);
scanf("%s", c + 1);
int u = 0;
for (int i = 1; i <= n; ++i) {
bool fl = (c[i] == '1') && u;
u ^= (c[i] - '0');
if (i != 1) putchar(fl ? '-' : '+');
}
putchar('\n');
}
}
1774B - Coloring
Idea: Cirno_9baka
First, We can divide $$$n$$$ cells into $$$\left\lceil\frac{n}{k}\right\rceil$$$ segments that except the last segment, all segments have length $$$k$$$. Then in each segment, the colors in it are pairwise different. It's easy to find any $$$a_i$$$ should be smaller than or equal to $$$\left\lceil\frac{n}{k}\right\rceil$$$.
Then we can count the number of $$$a_i$$$ which is equal to $$$\left\lceil\frac{n}{k}\right\rceil$$$. This number must be smaller than or equal to $$$n \bmod k$$$, which is the length of the last segment.
All $$$a$$$ that satisfies the conditions above is valid. We can construct a coloring using the method below:
First, we pick out all colors $$$i$$$ that $$$a_i=\left\lceil\frac{n}{k}\right\rceil$$$, then we use color $$$i$$$ to color the $$$j$$$-th cell in each segment.
Then we pick out all colors $$$i$$$ that $$$a_i<\left\lceil\frac{n}{k}\right\rceil-1$$$ and use these colors to color the rest of cells with cyclic order(i.e. color $$$j$$$-th cell of the first segment, of second the segment ... of the $$$\left\lceil\frac{n}{k}\right\rceil$$$ segment, and let $$$j+1$$$. when one color is used up, we begin to use the next color)
At last, we pick out all colors $$$i$$$ that $$$a_i=\left\lceil\frac{n}{k}\right\rceil-1$$$, and color them with the cyclic order.
This method will always give a valid construction.
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n, m, k;
scanf("%d %d %d", &n, &m, &k);
int fl = 0;
for (int i = 1; i <= m; ++i) {
int a;
scanf("%d", &a);
if (a == (n + k - 1) / k) ++fl;
if (a > (n + k - 1) / k) fl = 1 << 30;
}
puts(fl <= (n - 1) % k + 1 ? "YES" : "NO");
}
}
1774C - Ice and Fire
Idea: Little09
We define $$$f_i$$$ to mean that the maximum $$$x$$$ satisfies $$$s_{i-x+1}=s_{i-x+2}=...=s_{i}$$$.
It can be proved that for $$$x$$$ players, $$$f_{x-1}$$$ players are bound to lose and the rest have a chance to win. So the answer to the first $$$i$$$ battles is $$$ans_i=i-f_i+1$$$.
Next, we prove this conclusion. Suppose there are $$$n$$$ players and $$$n-1$$$ battles, and $$$s_{n-1}=1$$$, and there are $$$x$$$ consecutive $$$1$$$ at the end. If $$$x=n-1$$$, then obviously only the $$$n$$$-th player can win. Otherwise, $$$s_{n-1-x}$$$ must be 0. Consider the following facts:
Players $$$1$$$ to $$$x$$$ have no chance to win. If the player $$$i$$$ ($$$1\le i\le x$$$) can win, he must defeat the player whose temperature value is lower than him in the last $$$x$$$ battles. However, in total, only the $$$i-1$$$ player's temperature value is lower than his. Because $$$i-1<x$$$, the $$$i$$$-th player cannot win.
Players from $$$x+1$$$ to $$$n$$$ have a chance to win. For the player $$$i$$$ ($$$x+1\le i\le n$$$), we can construct: in the first $$$n-2-x$$$ battles, we let all players whose temperature value in $$$[x+1,n]$$$ except the player $$$i$$$ fight so that only one player will remain. In the $$$(n-1-x)$$$-th battle, we let the remaining player fight with the player $$$1$$$. Since $$$s_{n-1-x}=0$$$, the player $$$1$$$ will win. Then there are only the first $$$x$$$ players and the player $$$i$$$ in the remaining $$$x$$$ battles, so the player $$$i$$$ can win.
For $$$s_{n-1}=0$$$, the situation is similar and it will not be repeated here.
#include <bits/stdc++.h>
using namespace std;
const int N = 300005;
int T, n, ps[2];
char a[N];
void solve() {
scanf("%d %s", &n, a + 1);
ps[0] = ps[1] = 0;
for (int i = 1; i < n; ++i) {
ps[a[i] - 48] = i;
if (a[i] == '0')
printf("%d ", ps[1] + 1);
else
printf("%d ", ps[0] + 1);
}
putchar('\n');
}
int main() {
scanf("%d", &T);
while (T--) solve();
return 0;
}
1774D - Same Count One
Idea: mejiamejia and AquaMoon
Considering that we need to make the number of $$$1\text{s}$$$ in each array the same, we should calculate the sum of $$$1\text{s}$$$, and every array has $$$sum / n$$$ $$$1\text{s}$$$. Because only the same position of two different arrays can be selected for exchange each time, for a position $$$pos$$$, we traverse each array each time. If the number of $$$1\text{s}$$$ in this array is not enough, then we need to turn some $$$0\text{s}$$$ into $$$1\text{s}$$$; If the number of $$$1\text{s}$$$ in this array is more than we need, then some $$$1\text{s}$$$ should be turned into $$$0\text{s}$$$. It can be proved that as long as the total number of $$$1\text{s}$$$ is a multiple of $$$n$$$, the number of $$$1\text{s}$$$ in each array can be made the same through exchanges.
#include <bits/stdc++.h>
int main() {
int T;
scanf("%d", &T);
while (T--) {
int n, m;
scanf("%d %d", &n, &m);
std::vector<std::vector<int>> A(n, std::vector<int>(m, 0));
std::vector<int> sum(n, 0);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
scanf("%d", &A[i][j]);
sum[i] += A[i][j];
}
}
int tot = 0;
for (int i = 0; i < n; ++i) tot += sum[i];
if (tot % n) {
puts("-1");
continue;
}
tot /= n;
std::vector<std::tuple<int, int, int>> ans;
std::vector<int> Vg, Vl;
Vg.reserve(n), Vl.reserve(n);
for (int j = 0; j < m; ++j) {
for (int i = 0; i < n; ++i) {
if (sum[i] > tot && A[i][j]) Vg.push_back(i);
if (sum[i] < tot && !A[i][j]) Vl.push_back(i);
}
for (int i = 0; i < (int)std::min(Vl.size(), Vg.size()); ++i) {
++sum[Vl[i]], --sum[Vg[i]];
ans.emplace_back(Vl[i], Vg[i], j);
}
Vl.clear(), Vg.clear();
}
printf("%d\n", (int)ans.size());
for (auto [i, j, k] : ans) printf("%d %d %d\n", i + 1, j + 1, k + 1);
}
return 0;
}
1774E - Two Chess Pieces
Idea: Cirno_9baka
We can find that for any $$$d$$$-th ancestor of some $$$b_i$$$, the first piece must pass it some time. Otherwise, we will violate the distance limit. The second piece must pass the $$$d$$$-th ancestor of each $$$b_i$$$ as well. Then we can add the $$$d$$$-th ancestor of each $$$a_i$$$ to the array $$$b$$$, and add the $$$d$$$-th ancestor of each $$$b_i$$$ to the array $$$a$$$.
Then we can find now we can find a solution that each piece only needs to visit its nodes using the shortest route, without considering the limit of $$$d$$$, and the total length can be easily computed. We can find that if we adopt the strategy that we visit these nodes according to their DFS order(we merge the array of $$$a$$$ and $$$b$$$, and sort them according to the DFS order, if the first one is from $$$a$$$, we try to move the first piece to this position, otherwise use the second piece), and move the other piece one step closer to the present piece only if the next step of the present piece will violate the distance limit, then we can ensure the movement exactly just let each piece visit its necessary node without extra operations.
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int t[N * 2], nxt[N * 2], cnt, h[N];
int n, d;
void add(int x, int y) {
t[++cnt] = y;
nxt[cnt] = h[x];
h[x] = cnt;
}
int a[N], b[N];
bool f[2][N];
void dfs1(int x, int fa, int dis) {
a[dis] = x;
if (dis > d)
b[x] = a[dis - d];
else
b[x] = 1;
for (int i = h[x]; i; i = nxt[i]) {
if (t[i] == fa) continue;
dfs1(t[i], x, dis + 1);
}
}
void dfs2(int x, int fa, int tp) {
bool u = 0;
for (int i = h[x]; i; i = nxt[i]) {
if (t[i] == fa) continue;
dfs2(t[i], x, tp);
u |= f[tp][t[i]];
}
f[tp][x] |= u;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> d;
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
add(x, y), add(y, x);
}
dfs1(1, 0, 1);
for (int i = 0; i <= 1; i++) {
int num;
cin >> num;
for (int j = 1; j <= num; j++) {
int x;
cin >> x;
f[i][x] = 1, f[i ^ 1][b[x]] = 1;
}
}
for (int i = 0; i <= 1; i++) dfs2(1, 0, i);
int ans = 0;
for (int i = 0; i <= 1; i++)
for (int j = 2; j <= n; j++)
if (f[i][j]) ans += 2;
cout << ans;
return 0;
}
1774F1 - Magician and Pigs (Easy Version)
Idea: Little09
Let $$$X=\max x$$$.
Think about what ‘Repeat’ is doing. Assuming the total damage is $$$tot$$$ ($$$tot$$$ is easy to calculate because it will be multiplied by $$$2$$$ after each ‘Repeat’ and be added after each ‘Attack’). After repeating, each pig with a current HP of $$$w$$$ ($$$w > tot$$$) will clone a pig with a HP of $$$w-tot$$$.
Why? ‘Repeat’ will do what you just did again, so each original pig will certainly create a pig the same as it, and it will be attacked by $$$tot$$$, so it can be considered that a pig with $$$w-tot$$$ HP has been cloned.
Next, the problem is to maintain a multiset $$$S$$$, which supports: adding a number, subtracting $$$x$$$ for all numbers, and inserting each number after subtracting $$$tot$$$. Find the number of positive elements in the final multiset.
$$$tot$$$ in ‘Repeat’ after the first ‘Attack’ will multiply by $$$2$$$ every time, so it will exceed $$$X$$$ in $$$O(\log X)$$$ times. That is, only $$$O(\log X)$$$ ‘Repeat’ operations are effective. So we can maintain $$$S$$$ in brute force. Every time we do ‘Repeat’, we take out all the numbers larger than $$$tot$$$, then subtract and insert them again. Note that we may do some ‘Repeat’ operations when $$$tot=0$$$, which will result in the number of pigs generated before multiplying by $$$2$$$. Therefore, we also need to maintain the total multiplication.
If you use map to maintain it, the time complexity is $$$O((n+X)\log ^2X)$$$. It can pass F1. You can also use some ways to make the time complexity $$$O((n+X)\log X)$$$.
// Author: Little09
// Problem: F. Magician and Pigs (Easy Version)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 998244353, inv = (mod + 1) / 2;
int n;
map<ll, ll> s;
ll tot, mul = 1, ts = 1;
inline void add(ll &x, ll y) { (x += y) >= mod && (x -= mod); }
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
while (n--) {
int op;
cin >> op;
if (op == 1) {
ll x;
cin >> x;
add(s[x + tot], ts);
} else if (op == 2) {
ll x;
cin >> x;
tot += x;
} else if (tot <= 2e5) {
if (tot == 0)
mul = mul * 2 % mod, ts = ts * inv % mod;
else {
for (ll i = tot + 2e5; i > tot; i--) add(s[i + tot], s[i]);
tot *= 2;
}
}
}
ll res = 0;
for (auto i : s)
if (i.first > tot) add(res, i.second);
res = res * mul % mod;
cout << res;
return 0;
}
1774F2 - Magician and Pigs (Hard Version)
Idea: Little09
For F1, there is another way. Consider every pig. When Repeat, it will clone, and when Attack, all its clones will be attacked together. Therefore, considering all the operations behind each pig, you can choose to reduce $$$x$$$ (the current total damage) or not when Repeat, and you must choose to reduce $$$x$$$ when Attack. Any final choice will become a pig (living or not).
We just need to calculate how many Repeat choices can make a living pig. For Repeat of $$$x=0$$$, there is no difference between the two choices. For the Repeat of $$$x\geq 2\times 10^5$$$, it is obvious that you can only choose not to reduce $$$x$$$. Except for the above parts, there are only $$$O(\log x)$$$ choices. You can just find a subset or use knapsack to solve it. It can also pass F1 and the time complexity is $$$O((n+X)\log X)$$$.
The bottleneck of using this method to do F2 lies in the backpack. The problem is that we need to find how many subsets whose sum $$$<x$$$ of of a set whose size is $$$O(\log X)$$$.
Observation: if you sort the set, each element is greater than the sum of all elements smaller than it. We can use observation to solve the problem. Consider each element from large to small. Suppose you now need to find elements and subsets of $$$<x$$$. If the current element $$$\ge x$$$, it must not be selected; If the current element $$$<x$$$, if it is not selected, the following elements can be selected at will (the sum of all the following elements is less than it). It can be recursive. Thus, for a given $$$x$$$, we can find the number of subsets whose sum $$$<x$$$ within $$$O(\log X)$$$.
The time complexity is $$$O(n\log X)$$$.
// Author: Little09
// Problem: F. Magician and Pigs
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mem(x) memset(x, 0, sizeof(x))
#define endl "\n"
#define printYes cout << "Yes\n"
#define printYES cout << "YES\n"
#define printNo cout << "No\n"
#define printNO cout << "NO\n"
#define lowbit(x) ((x) & (-(x)))
#define pb push_back
#define mp make_pair
#define pii pair<int, int>
#define fi first
#define se second
const ll inf = 1000000000000000000;
// const ll inf=1000000000;
const ll mod = 998244353;
// const ll mod=1000000007;
const int N = 800005;
int n, m;
ll a[N], b[N], c[N], cnt, s[N], d[N], cntd;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
ll maxs = 1e9, sum = 0;
for (int i = 1; i <= n; i++) {
cin >> a[i];
if (a[i] != 3) cin >> b[i];
if (a[i] == 2) sum += b[i];
sum = min(sum, maxs);
if (a[i] == 3) b[i] = sum, sum = sum * 2;
sum = min(sum, maxs);
}
sum = 0;
ll res = 1, ans = 0;
for (int i = n; i >= 1; i--) {
if (a[i] == 2)
sum += b[i];
else if (a[i] == 3) {
if (b[i] == maxs) continue;
if (b[i] == 0) {
res = res * 2 % mod;
continue;
}
c[++cnt] = b[i];
} else {
b[i] -= sum;
if (b[i] <= 0) continue;
ll su = 0, r = b[i];
for (int j = 1; j <= cnt; j++) {
if (r > c[j]) {
su = (su + (1ll << (cnt - j))) % mod;
r -= c[j];
}
}
su = (su + 1) % mod;
ans = (ans + su * res) % mod;
}
}
cout << ans;
return 0;
}
1774G - Segment Covering
Idea: ChthollyNotaSeniorious and JianfengZhu
If there exist two segments $$$(l_1, r_1), (l_2, r_2)$$$ such that $$$l_1 \le l_2 \le r_2 \le r_1$$$ and we choose $$$(l_1, r_1)$$$, number of ways of choosing $$$(l_2, r_2)$$$ at the same time will be equal to that of not choosing. Hence if we choose $$$(l_1, r_1)$$$, the signed number of ways will be $$$0$$$. So we can delete $$$(l_1, r_1)$$$.
It can be proved that the absolute value of every $$$f_{l,r} - g_{l,r}$$$ doesn't exceed $$$1$$$.
Proof: First, find segments $$$(l_i, r_i)$$$ which are completely contained by $$$(l, r)$$$.
Let us sort $$$(l_i, r_i)$$$ in ascending order of $$$l_i$$$. As there does not exist a segment that contains another, $$$r_i$$$ are also sorted.
Assume that $$$l_2 < l_3 \leq r_1$$$ and $$$r_3 \geq r_2$$$. If we choose segments $$$1$$$ and $$$3$$$, choosing $$$2$$$ or not will be the same except for the sign. So $$$3$$$ is useless. So we can delete such useless segments. After the process, $$$l_3 > r_1, l_4 > r_2, \cdots$$$ will be held. If $$$[l_1, r_1] \cup [l_2, r_2] \cup \cdots \cup [l_k, r_k] = [l, r]$$$, answer will be $$$(-1)^k$$$, else answer will be $$$0$$$.
This picture shows what the segments eventually are like:

For $$$[l_i, r_i]$$$, we can find the lowest $$$j$$$ such that $$$l_j > r_i$$$ and construct a tree by linking such $$$i$$$ and $$$j$$$. Then the LCA of $$$1$$$ and $$$2$$$ will be $$$5$$$, where the answer becomes 0.
So we can get the answer of $$$(ql, qr)$$$ quickly by simply finding the LCA of two segments -- the segment starting with $$$ql$$$ (if no segment starts with $$$ql$$$, the answer is $$$0$$$), and the first segment whose $$$l$$$ is greater than $$$ql$$$ (if it do not intersect with the previous segment, the answer is $$$0$$$).
And find the segment ending with $$$qr$$$. If it is on the path of the two segments, the answer will be $$$\pm 1$$$. Else, the answer will be $$$0$$$.
#include <bits/stdc++.h>
#define File(a) freopen(a ".in", "r", stdin), freopen(a ".out", "w", stdout)
using tp = std::tuple<int, int, int>;
const int sgn[] = {1, 998244352};
const int N = 200005;
int x[N], y[N];
std::vector<tp> V;
bool del[N];
int fa[20][N];
int m, q;
int main() {
scanf("%d %d", &m, &q);
for (int i = 1; i <= m; ++i)
scanf("%d %d", x + i, y + i), V.emplace_back(y[i], -x[i], i);
std::sort(V.begin(), V.end());
int mxl = 0;
for (auto [y, x, i] : V) {
if (-x <= mxl) del[i] = true;
mxl = std::max(mxl, -x);
}
V.clear();
x[m + 1] = y[m + 1] = 1e9 + 1;
for (int i = 1; i <= m + 1; ++i) {
if (!del[i]) V.emplace_back(x[i], y[i], i);
}
std::sort(V.begin(), V.end());
for (auto [x, y, id] : V) {
int t = std::get<2>(*std::lower_bound(V.begin(), V.end(), tp{y + 1, 0, 0}));
fa[0][id] = t;
}
fa[0][m + 1] = m + 1;
for (int k = 1; k <= 17; ++k) {
for (int i = 1; i <= m + 1; ++i) fa[k][i] = fa[k - 1][fa[k - 1][i]];
}
for (int i = 1; i <= q; ++i) {
int l, r;
scanf("%d %d", &l, &r);
int u = std::lower_bound(V.begin(), V.end(), tp{l, 0, 0}) - V.begin(), v = u + 1;
u = std::get<2>(V[u]);
if (x[u] != l || y[u] > r) {
puts("0");
continue;
}
if (y[u] == r) {
puts("998244352");
continue;
}
v = std::get<2>(V[v]);
if (y[v] > r || x[v] > y[u]) {
puts("0");
continue;
}
int numu = 0, numv = 0;
for (int i = 17; i >= 0; --i) {
if (y[fa[i][u]] <= r) {
u = fa[i][u];
numu += !i;
}
}
for (int i = 17; i >= 0; --i) {
if (y[fa[i][v]] <= r) {
v = fa[i][v];
numv += !i;
}
}
if (u == v || (y[u] != r && y[v] != r))
puts("0");
else
printf("%d\n", sgn[numu ^ numv]);
}
return 0;
}
1774H - Maximum Permutation
Idea: Ecrade_
When it seems to be hard to come up with the whole solution directly, simplified questions can often be a great helper. So first let us consider the case where $$$n$$$ is the multiple of $$$k$$$.
Let $$$t=\frac{n}{k}$$$.
What is the largest value one can obtain theoretically? Pick out $$$t$$$ subsegments $$$a_{[1:k]},a_{[k+1:2k]},\dots,a_{[n-k+1:n]}$$$, and one can see that the answer cannot be greater than the average value of the sum of each subsegment, that is $$$\frac{n(n+1)}{2t}=\frac{k(n+1)}{2}$$$.
Case 1: $$$k$$$ is even
If $$$k$$$ is even, one can construct $$$a=[1,n,2,n-1,3,n-2,\dots,\frac{n}{2},\frac{n}{2}+1]$$$ to reach the maximum value.
Case 2: $$$k$$$ is odd
For easy understanding let us put $$$a_{[1:k]},a_{[k+1:2k]},\dots,a_{[n-k+1:n]}$$$ into a $$$t\times k$$$ table from top to bottom like this:
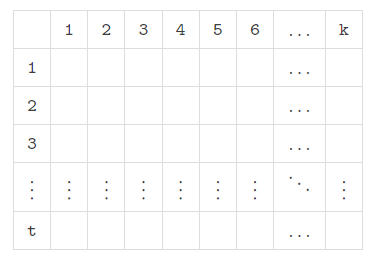
Note that the difference value between two consecutive subsegments is equal to the difference value between two values in the same column in this table. It inspires us to fill in the last $$$k-3$$$ columns in an S-shaped way like this:
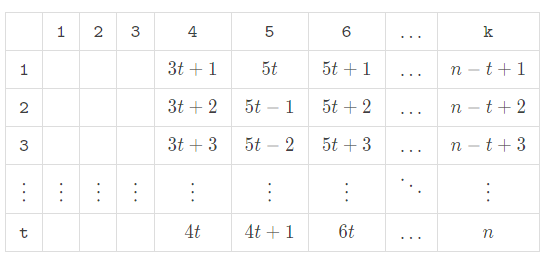
Then our goal is to split the remaining $$$3t$$$ numbers into $$$3$$$ groups and minimize the difference value between the sum of each group.
If $$$n$$$ is odd, the theoretical maximum value mentioned above is an integer, and the sum of each group must be equal to reach that value. Otherwise, the theoretical maximum value mentioned above is not an integer, and the sum of each group cannot be determined. So let us first consider the case where $$$n$$$ is odd. A feasible approach to split the numbers is as follows:
Then fill them into the table:
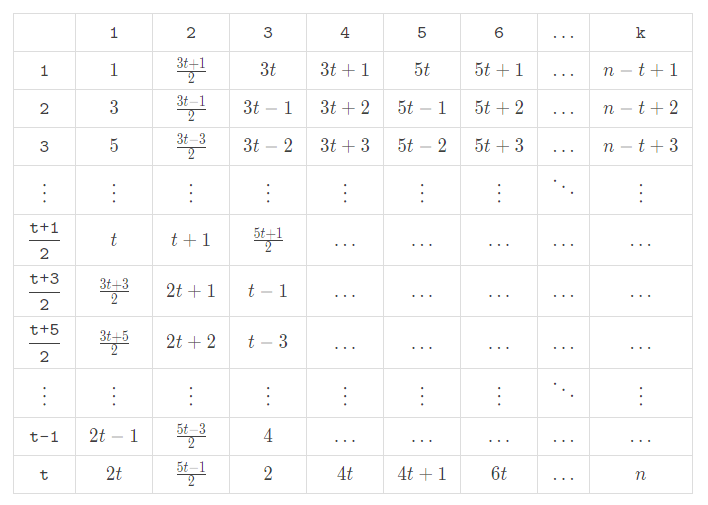
Similarly, one can come up with an approach when $$$n$$$ is even:
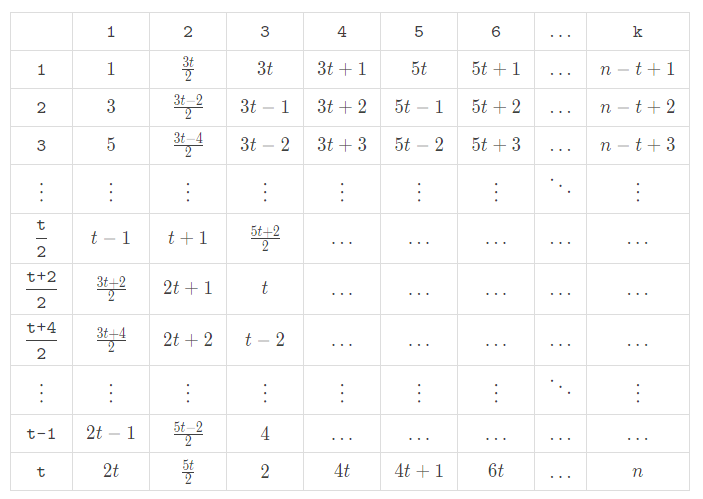
Okay, it's time for us to go back to the original problem.
Let $$$n=qk+r\ (r,q\in \mathbb{N},1\le r<k)$$$.
Split $$$n$$$ elements like this:
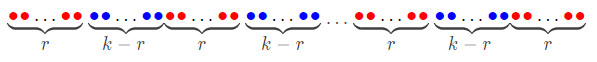
As shown in the picture, there are $$$(q+1)$$$ red subsegments with $$$r$$$ elements each, and $$$q$$$ blue subsegments with $$$(k-r)$$$ elements each. What is the largest value one can obtain theoretically now? Pick out $$$q$$$ non-intersecting subsegments consisting of a whole red subsegment and a whole blue segement each, and one can see that the answer cannot be greater than the average value of the sum of each subsegment, that is the sum of $$$1 \thicksim n$$$ subtracted by the sum of any whole red subsegment, then divide by $$$q$$$. Similarly, the answer cannot be greater than the sum of $$$1 \thicksim n$$$ added by the sum of any whole blue subsegment, then divide by $$$(q+1)$$$.
Thus, our goal is to make the maximum sum of each red subsegment the minimum, and make the minimum sum of each blue subsegment the maximum. Now here comes an interesting claim: it can be proved that,
If $$$r\neq 1$$$ and $$$k-r\neq 1$$$, one can fill the red subsegments using the method when $$$n$$$ is the multiple of $$$k$$$ (here $$$n'=(q+1)r,k'=r$$$ ) with $$$1\thicksim (q+1)r$$$, and the blue subsegments (here $$$n'=q(k-r),k'=k-r$$$ ) with the remaining numbers;
If $$$r=1$$$, one can fill the red subsegments with $$$1\thicksim (q+1)$$$ from left to right, and the first element of the blue subsegments with $$$(q+2)\thicksim (2q+1)$$$ from right to left, and the blue subsegments without the first element using the method when $$$n$$$ is the multiple of $$$k$$$ (here $$$n'=q(k-2),k'=k-2$$$ ) with the remaining numbers;
If $$$k-r=1$$$ and $$$q=1$$$, one can let $$$a_k=n$$$, and fill the rest two subsegments using the method when $$$n$$$ is the multiple of $$$k$$$ (here $$$n'=n-1,k'=k-1$$$ ) with the remaining numbers;
If $$$k-r=1$$$ and $$$q>1$$$, one can fill the blue subsegments with $$$(n-q+1)\thicksim n$$$ from right to left, and the first element of the red subsegments with $$$1\thicksim (q+1)$$$ from right to left, and the red subsegments without the first element using the method when $$$n$$$ is the multiple of $$$k$$$ (here $$$n'=(q+1)(r-1),k'=r-1$$$ ) with the remaining numbers,
then the constraints can both be satisfied and the value of the permutation is theoretically maximum. The proof is omitted here.
Time complexity: $$$O(\sum n)$$$
Bonus: solve the problem if $$$k\ge 2$$$.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll t,n,k,seq[100009],ans[100009];
inline ll read(){
ll s = 0,w = 1;
char ch = getchar();
while (ch > '9' || ch < '0'){ if (ch == '-') w = -1; ch = getchar();}
while (ch <= '9' && ch >= '0') s = (s << 1) + (s << 3) + (ch ^ 48),ch = getchar();
return s * w;
}
ll f(ll x,ll y,ll k){return (x - 1) * k + y;}
void get(ll n,ll k){
if (!(k & 1)){
for (ll i = 1;i <= n >> 1;i += 1) seq[(i << 1) - 1] = i,seq[i << 1] = n + 1 - i;
return;
}
ll m = n / k,cur = 3 * m;
for (ll i = 4;i <= k;i += 1){
if (i & 1) for (ll j = m;j >= 1;j -= 1) seq[f(j,i,k)] = ++ cur;
else for (ll j = 1;j <= m;j += 1) seq[f(j,i,k)] = ++ cur;
}
for (ll i = 1;i <= (m + 1 >> 1);i += 1){
seq[f(i,1,k)] = (i << 1) - 1;
seq[f(i,2,k)] = ((3 * m + 3) >> 1) - i;
seq[f(i,3,k)] = 3 * m - i + 1;
}
for (ll i = (m + 3 >> 1);i <= m;i += 1){
ll delta = i - (m + 3 >> 1);
seq[f(i,1,k)] = ((3 * m + 3) >> 1) + delta;
seq[f(i,2,k)] = (m << 1) + 1 + delta;
seq[f(i,3,k)] = m - (m & 1) - (delta << 1);
}
}
void print(){
ll res = 0,sum = 0;
for (ll i = 1;i <= k;i += 1) sum += ans[i];
res = sum;
for (ll i = k + 1;i <= n;i += 1) sum += ans[i] - ans[i - k],res = min(res,sum);
printf("%lld\n",res);
for (ll i = 1;i <= n;i += 1) printf("%lld ",ans[i]);
puts("");
}
int main(){
t = read();
while (t --){
n = read(),k = read();
if (!(n % k)){
get(n,k);
for (ll i = 1;i <= n;i += 1) ans[i] = seq[i];
print();
continue;
}
ll q = n / k,r = n % k;
if (r == 1){
ll cur = 0,delta = (q << 1) + 1;
for (ll i = 1;i <= n;i += k) ans[i] = ++ cur;
for (ll i = n - k + 1;i >= 2;i -= k) ans[i] = ++ cur;
get(q * (k - 2),k - 2),cur = 0;
for (ll i = 3;i <= n;i += k) for (ll j = i;j <= i + k - 3;j += 1) ans[j] = seq[++ cur] + delta;
print();
continue;
}
if (k - r == 1){
if (q == 1){
ll cur = 0;
ans[k] = n;
get(n - 1,k - 1);
for (ll i = 1;i < k;i += 1) ans[i] = seq[++ cur];
for (ll i = k + 1;i <= n;i += 1) ans[i] = seq[++ cur];
print();
continue;
}
ll cur = n + 1,delta = q + 1;
for (ll i = k;i <= n;i += k) ans[i] = -- cur;
cur = 0;
for (ll i = 1;i <= n;i += k) ans[i] = ++ cur;
get((q + 1) * (r - 1),r - 1),cur = 0;
for (ll i = 2;i <= n;i += k) for (ll j = i;j <= i + r - 2;j += 1) ans[j] = seq[++ cur] + delta;
print();
continue;
}
ll cur = 0,delta = (q + 1) * r;
get((q + 1) * r,r);
for (ll i = 1;i <= n;i += k) for (ll j = i;j <= i + r - 1;j += 1) ans[j] = seq[++ cur];
get(q * (k - r),k - r),cur = 0;
for (ll i = r + 1;i <= n;i += k) for (ll j = i;j <= i + (k - r) - 1;j += 1) ans[j] = seq[++ cur] + delta;
print();
}
return 0;
}










Auto comment: topic has been updated by ChthollyNotaSeniorious (previous revision, new revision, compare).
Thanks for fast tutorial.
Problem B was decent!!
Enlighten me what decency you found ?
Is it possible to solve Problem E if they don't have to return to the root?
The implementation would be painful.
We can see answer >= (answer of the original problem) — 2*(sum of max depth of target nodes of 2 pieces), but if there's no 2 deepest target nodes of each piece where their distance <=d, it's hard to find the minimum number of operations
I didn't realize initially that they did have to return to the initial spot, so I solved it the other way. It was more complicated and I had to remove that complication to get the right answers.
But the additional complication wasn't especially tough. Just required a lot of attention to small details.
DD_my_love solved one problem less than me still has a better rank by around 300. Don't know how many more candidates are like this. LMAO ded.
1774A - Add Plus Minus Sign
It can be solve in O(t * n). the solution sounds like this: Let's create a sum equal to the first element. Then we just subtract 1 if sum > 0, otherwise we add 1.
AC Code: 185664996
Alternative solution for E: We define dp[x] as minimum cost to visit all subtree nodes of x with both pieces and come back. We do DFS, maintaining two values — mn1[v] and mn2[v] — which signify the maximum depth of a vertex we has to be visited by the first piece or the second piece. Now let's do transitions from a vertex u which is a son of v to v: if there are both types of vertexes (which have to be visited by both pieces) we do dp[v] += (4 + dp[u]) (we have to come down, visit all vertices and then come back)
if there are no vertexes, we simply don't have to visit that subtree.
if there is one type (let's say type 1 — a vertex that has to be visited by the first piece), then we have to visit that subtree with the corresponding piece (dp[v] += (2 + dp[x]), and, if we have to come down with the other piece, we do dp[v] += 2 (and that is why we maintain both heights)
code: https://mirror.codeforces.com/contest/1774/submission/185696139
If we add another dimension to the DP, can we solve this problem?
https://mirror.codeforces.com/blog/entry/110184?#comment-981781
[Deleted] (Whatever I suggested is not correct)
There is no need in dp: you can just do ans += 2 or 4 if you need to visit some child. My implementation: 185696308
lol
ChthollyNotaSeniorious there is some problem with markup in the solution for D
fixed now
Problem B was underrated, it was a much better problem to be at B
I knew I had a problem with how I was approaching B so I looked at the other problems instead of trying to force it.
Then I came back in 30 minutes and wrote a good easy solution. Sometimes it's important to recognize when you're on the wrong path, even when it seems to be working.
Got you! Problem B taught us to be focussed more on the basics
Thanks for the super fast editorial....
Is it just me or latex for D doesn't work?
Fixed
is there any working score predictor for codeforces contest ?
I use Carrot. It's really accurate.
yep, carrot extension
Problem B had very weak pretests which lead to a lot of people getting hacked so some people flew up the ranks by hacking instead of solving more questions
dont know what is going with the solution of b in editorial if anyone interested in a single line solution do check this out https://mirror.codeforces.com/contest/1774/submission/185703602
can u paste ur code here, I cant view it
can you please explain why did we add arr.count(max(arr)) into the expression?
like lets say we have multiple maximums than to fits those maximum we need count of maximum extra space .
for example 1 2 7 7 than to fit these two 7s we need to use count of the maximum element
Understood, thanks :)
Can anyone view the solutions of other participants now? I aint able to view it
It was a good round and I liked it.
An occasional problem without strong pre-tests like B is a good thing because it offers opportunities to hackers. Those who made mistakes learn a valuable lesson about being more careful.
Pre-tests are not supposed to be a guarantee.
Problem E was very good.
The code for E is quite hard to understand compared to the written description which was crystal clear. It would be great if OP can use better variable naming in the future to help with readability.
A slightly different solution to F: 185721355
For every Create operation, we will find the number of pigs that survive. Let the index of the current Create operation be $$$i$$$. For now, we will assume that there was an Attack operation before $$$i$$$. We will create an array $$$s$$$: for $$$j >= 2$$$, $$$s_j$$$ will be the sum of Attack values between the $$$j-1$$$-th and $$$j$$$-th Remove to the right of $$$i$$$. $$$s_1$$$ will be the sum of Attack values between $$$i$$$ and the first remove to the right, and $$$s_0$$$ will be equal to the sum of Attack values before $$$i$$$ (so $$$s_0 > 0$$$). As we are only interested in the first $$$logX$$$ Repeats after $$$i$$$, we will only be interested in the first $$$t \leq O(logX)$$$ elements of this array. We will also denote $$$y$$$ to be the sum of Attack values after the last "interesting" Repeat.
The array $$$s$$$ and the value $$$y$$$ are enough to find the solution for pig $$$i$$$: among all its clones, the health of the one with the $$$k$$$-th largest HP ($$$0$$$-indexed) turns out to be $$$x_i - s_0*k - y - \sum_{1\leq j < t} s_j * (\lfloor \frac{k}{2^{j-1}} \rfloor + 1)$$$. I can't think of a simple proof for this, but it's easy to see if you write the "unwrapped" (as in, you actually copy the sequence in case of a Repeat) sequence of operations down. Anyway, this means we can do a binary search to find the smallest positive element.
In case of $$$s_0 = 0$$$ (if there was no Attack before $$$i$$$), we also need to count the number of Repeats before the next Attack, and multiply the answer accordingly.
This is technically $$$O(Nlog^2 X)$$$, but it passes F2 in just over a second and I haven't managed to hack it yet, so it's probably just optimized enough.
I think your key formulation for "kth largest HP" aligns with the key observation in the tutorial. Essentially, because of the observation that the damage of clones is "greedy", we can always find the kth largest "subset sum" of clones (two ways to count this value: one is counting by clones, as the tutorial does; the other is counting by attacks, as in your formula). : )
Thanks for providing another idea! The property of this problem is very intriguing.
Could anyone help me with Problem F1? I'm not sure why my solution doesn't work. Basically, I track all operations performed in an array of pairs ("ops"). I track the total decrease in the int "total" which I minimize with "SIZE" (a const int = 2e5+5) to avoid overflow.
If total == size when I encounter the third operation, I simply don't track the operation because all previous pigs will be killed, and all newly created pigs will be created in the same way as the first set was. If total < SIZE and total > 0, then I double all of the operations in "ops" and double total. If total == 0, I record that the count of all current pigs should be doubled.
I use prefix sums to calculate how many times each created pig will be doubled or have its health decreased.
Here is my submission: https://mirror.codeforces.com/contest/1774/submission/185734070
Thanks in advance.
Strange. We've made many hacks but there are only 18 testcases in the problem now.
Problems are good.
In problem E you can also just simulate all their moves:
C was easy but I was panik by B and ended up solving only A :(
dude can you explain problem C's idea
Store max and min index of iTH game winner. If game iTH is "0", all player from 1 -> max[i-1] will win the game, otherwise is min[i-1] + 1 -> i. You can prove it yourself.
Can someone give better explanation for problem C. The intuition behind the solution and observation.
I don't understand editorial. I'll just explain my solution.
Suppose we want to answer on $$$x$$$, so we consider only first $$$x - 1$$$ rounds. Then, following holds for any $$$y \leq x$$$. After $$$y - 1$$$ rounds there are $$$y - 1$$$ who dropped out. And one participant who is current winner. We can get their temperature, including winner. Length of this list will be $$$y$$$. Then sort this list in increasing order. Now, crucial part, if we change their temperature into consecutive numbers from $$$1$$$ to $$$y$$$, and let them perform rounds from the beginning in the same order, we will get same winner (but probably now he has different (new) temperature). This means, that first $$$y$$$ rounds for any limit $$$x$$$ has outcome similar to limit $$$y$$$, just some participants ignored. But in any outcome with limit $$$y$$$ we can insert all ignored participants and get same outcome as if it was limit $$$x$$$.
Let's apply it for $$$x = n$$$ and $$$y = n - 1$$$. This means, only one participant is ignored, the one who will fight winner of all previous rounds. Consider case when corresponding $$$s = 1$$$. There are two cases: either winner previous winner wins or new participant wins.
Suppose new participant wins with temperature $$$t$$$. Then temperature of previous winner is less than new one. So, there exist outcome where participant with less temperature is winner previous rounds. It means, set of possible winners with less temperature than $$$t$$$ is not empty set, so there is minimum temperature, who can win previous $$$n - 2$$$ rounds. In short: if new participant win, there is possible outcome where he wins against opponent with minimum temperature. Then, again crucial part: if we order all $$$y = n - 1$$$ participants by increasing temperature, we know where new participant is inserted. And, to be able to win, he should be inserted after winner of previous rounds (after participant who can win $$$y - 1 = n - 2$$$ rounds with minimum possible temperature). This gives us way to find out who could win against winner of previous rounds if we know minimum possible winner of $$$n - 2$$$ rounds.
Second case: suppose previous winner wins against new participant. Similarly, we know where new participant should be inserted in sorted list of participants of $$$n - 2$$$ rounds. It should be inserted before previous winner. And obvious best way is to insert him as participant with temperature 1, then he can be defeated by any previous winner (because all their temperatures will be greater than 1). This gives us way to find out who could win against new participant if we know possible winners of $$$n - 2$$$ rounds.
Let all possible winners of $$$y - 1 = n - 2$$$ rounds without new inserted participant is $$$W$$$. To clarify: W is set of who could win if there was $$$n - 1$$$ participant with temperatures from $$$1$$$ to $$$n - 1$$$. Then, using two observations above, we get that possible winners of $$$n$$$ rounds is all participants with temperatures $$$> \min(W)$$$ and also $$$v + 1$$$ for each $$$v \in W$$$ (after insertion of new participant under temperature 1, all previous winners increase their temperature). It's easy to show that union of this two sets is just every temperature $$$v$$$ satisfying: $$$\min(W) < v \leq n$$$.
Similarly, we can find out, if corresponding $$$s$$$ is 0 and winners of previous $$$n - 1$$$ rounds is $$$W$$$, then winners of $$$n$$$ rounds is every temperature $$$v$$$ satisfying: $$$1 \leq v \leq \max(W)$$$.
Using this two relationships, we can maintain possible winners as segment and update it correspondingly and output answer based on segment length.
Source code: 185679312
Who can prove D's conclusion for me, why I don't feel so obvious?
hello i did not get time to solve d in the contest but today i solved it without seeing the editorial, i'll tell you my implemetation. 1.)firsly we count the total number of ones in the (n*m) array, let's name it check, now we will like to distribute equal number of ones in all the n rows, now if check%n is not equal to 0, then we can not have our answer, otherwise we will like to distribute (check/n) number of ones to all the n rows, let's call this number req. 2.)now in all the n rows we will calculate the total number of ones present in it if it is greater than req, we will store the index of the row and the value in a map, and all the values less than req in another map and we will not touch the rows which have req no of ones, this can be done in (n*m) complexity which is allowed. 3.)now our task is to exchange ones between the rows which has smaller no of ones than required and with the ones which have larger number of ones required, note we already know about them in our two maps, both the index and the values, this can be done easily in ((n^2)*m) complexity by going row by row but sadly it is not allowed, here comes the tricky part:-> 4.)instead of going row by row we go column by column, each time we encounter a one in our column we will check if the row in which the one occurs is a row having larger number of ones than req using map, if yes we mark it and if we find a corresponding 0 for that one on the same column whose row has lesser number of ones than req, we exchange the value, vice versa goes for when we encounter a 0 and after the row having larger number of ones than required becomes equal to required we erase it from the map, vice versa for the row having lesser number of ones than required, this complexity for this process is order of n*m which is allowed, ignoring the logarithmic time complexities used for map. here is my submission: https://mirror.codeforces.com/contest/1774/submission/185759065
Hello everyone I am not able to understand the logic of question number d (same count one) from the tutorial. Can anyone explain the logic behind the d. I dont want to see the solution for d now because i want to try it first. Thank You...
step1: find out all rows which have an excess of 1's and which have deficient 1's
Swapping between ith, jth row in the kth column becomes valid only when a[i][k] != a[j][k] otherwise, after swapping, we will have the same matrix as before
We need to minimize the operations.
My claim :
Given a row with excess 1's and another row with deficient of 1's, it is always possible to send one from the excess row to the deficient row. (i.e sum[excess_row] --; sum[deff_row] ++; )
Proof :
(By contradiction)
Assume that you cannot do such swapping
Let any excess row contain x1 ones
Let any deficient row contain x2 ones
=> x1 > (sum/n) > x2
If I cannot do such a swapping, it means that for every 1 in excess_row, the corresponding column in the deficient_row should also contain a 1.
This implies
=> deficient row should contain at least x1 ones => x2 >= x1 But x1 > x2 This contradicts
Our claim is correct
thanks a lot for the proof. I had an intuition, but not being able to proof was really bugging me. Thanks again.
you are the first person to reply to me , welcome pa
Any E solution in easy words?
I'll try my hand at it.
To make the problem a bit nicer to explain (imo), I'll label the $$$a_1,a_2, \dotsc ,a_{m_1}$$$ nodes as red and the $$$b_1,b_2, \dotsc ,b_{m_2}$$$ ones as green.
We know that both nodes start at 1 and must return to 1, and so it's a good idea to root our tree at 1 as well. Let's consider an easier variant of the problem, where we only need to reach the red nodes.
So first off, since the nodes must return to 1, we notice that every edge in the optimal paths is traversed twice (one to go, and one to return) for each of our pieces.
If $$$d = n$$$, then we can simply keep the green piece back home at the root and let the red piece dance about. Let's suppose we know for each node whether it contains a red node in its subtree. Then it's clear that the minimum path that hits all red nodes AND returns to the root will traverse only the nodes that contain red nodes in its subtree. Crucially, it will traverse the edges twice and only twice (any more would be a waste).
Okay, that's great, now let's see what happens if $$$d < n$$$. So, the green piece must follow the red piece within a certain distance like a leashed dog. Now, we want to move the green piece minimally. So what we can do is greedily move a green piece only if we need to. What do I mean by this?
Let's assume we are at a root $$$r$$$ and both the red piece and green piece are here. Suppose $$$r$$$ has a child $$$c$$$ that has both green and red nodes in its subtree. We most definitely need to move both the green piece and red piece in that direction. (because we need to collect the green and red nodes). Thus, both red and green pieces traverse the edge from $$$r$$$ to its special child $$$c$$$, and we know that it must return back to the root (so it's gotta come back the way it came). Therefore, we can add $$$2$$$ for each piece, totaling to $$$4$$$ moves.
Now, let's suppose $$$r$$$'s child $$$c$$$ only contains a red node in its subtree. Well, let's suppose we know the depth of the deepest red node in this subtree. If this depth $$$\text{maxDepth} \leqslant d+\text{depth}(r)$$$, then we clearly don't need to move the green piece. The red piece can do it all by itself. We can add $$$2$$$ for the red piece and recurse further into the subtree. Notice this also holds for the reverse case ($$$c$$$ only contains a green node in its subtree), aka WLOG.
What if $$$\text{maxDepth} > d+\text{depth}(r)$$$? Well, we're gonna have to move the green piece in the direction of $$$c$$$, otherwise we violate the constraint. Note that this is very similar to the "+4" case where both red and green were contained in the subtree at $$$c$$$. So just like that, we add 4 and recurse further.
We basically apply these two principles to every child and do a proper DFS through it. Now the question is, how do we calculate
You can do this in any number of ways but I find it easiest to just do a DFS beforehand to set everything up. Set up an int array
maxRedDepthand when DFS'ing, if a node $$$v$$$ is red, then setmaxRedDepth[v] = depth. Then take the $$$\max($$$maxRedDepth[c]$$$)$$$ of every child.185894910
Detailed explanation. Thanks.
when in your explanation, maxDepth > d + depth(r)? , are we assuming that the green piece and red piece are at the same place ?
Yep.
i am still not able to process it clearly, can you please simulate it over an example to help me understand clearly, like when +2 extra steps can help us when maxDepth > d + depth(r) can be greater than just one edge distance?
Imagine that the tree is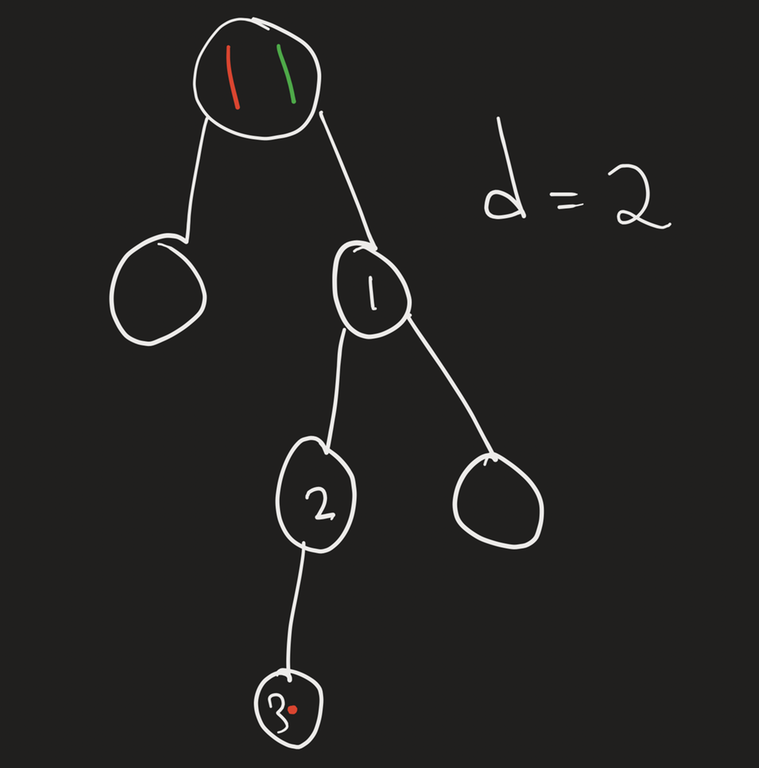
with $$$d = 2$$$, then it's clear that the red piece can't reach node 3 if the green piece doesn't move to 1.
maxDepth of 1 will be 2, as the red node 3 is 2 levels down from node 1.
why in problem B we are doing (n-1)%k +1 instead of n%k. Any Particular reason???.
if n is a multiple of k, it should be k instead of 0
1774B - Coloring how to prove that number of $$$a_i$$$ which is equal to $$$\left\lceil \frac{n}{k} \right\rceil$$$ should be not bigger than remainder?
How to make sure construction works? Not for all segments there is $$$j$$$-th cell. Do we just skip segment if $$$j$$$-th cell doesn't exist?
For a particular value of $$$k$$$, the number of segments $$$=$$$ $$$\lceil{\frac{n}{k}}\rceil$$$. Let's take $$$n = 12,$$$ $$$k=5$$$, then our segments will look like $$$[ __, __, __, __, __ ]$$$ $$$[ __, __, __, __, __ ]$$$ $$$[ __, __ ]$$$.
Here $$$\lceil{\frac{n}{k}}\rceil = \lceil{\frac{12}{5}}\rceil = 3$$$
Let $$$M[4] = [3, 3, 3, 2, 2, 2] = [a_1, a_2, a_3, a_4, a_5]$$$. Let's start filling the segment:
After filling $$$a_1$$$:
Segment $$$=$$$ $$$[ a_1, __, __, __, __ ]$$$ $$$[ a_1, __, __, __, __ ]$$$ $$$[ a_1, __ ]$$$
$$$M[4] = [0, 3, 3, 2, 2, 2] = [a_1, a_2, a_3, a_4, a_5]$$$.
After filling $$$a_2:$$$
Segment $$$=$$$ $$$[ a_1, a_2, __, __, __ ]$$$ $$$[ a_1, a_2, __, __, __ ]$$$ $$$[ a_1, a_2 ]$$$
$$$M[4] = [0, 0, 3, 2, 2, 2] = [a_1, a_2, a_3, a_4, a_5]$$$.
Now you see that there is no way to fill $$$a_3$$$ such that the distance between any two $$$a_3$$$ is $$$k$$$.
Hope this answers your question
maybe it doesn't work just because very first arrangement of $$$a_1$$$ is already wrong, and if you put them in other way, it will somehow turn out. I don't need "see" explanations, I need rigorous one.
How is the first arrangement of $$$a_1$$$ wrong? Since $$$a_1$$$ has the maximum frequency, it makes sense to handle it first and place it at the first position of the first segment since this position will definitely provide the distance of $$$k$$$ in the next subsequent segments.
There is also: following possibilities
Why you arguing about first one. May be for one of other it will work?
First of all, notice that your second arrangement is wrong since you won't be able to place $$$a_2$$$.
Hmmm, okay let me phrase it like this:
Let $$$K'$$$ $$$=$$$ $$$(n \% k \equiv 0$$$ $$$?$$$ $$$k : n \% k)$$$ --> The size of the last segment.
Let the suitable indexes in the $$$last$$$ segment be $$$[1, K']$$$
The only way to place first $$$K'$$$ elements having value equal to $$$\lceil\frac{n}{k}\rceil$$$ in the $$$last$$$ segment is to place them in the suitable indexe of the $$$last$$$ segment. After you have placed them in the $$$last$$$ segment, one sure way to place them in the remaining segments without violating any condition is to place them cyclically at distance $$$k$$$. Now we have $$$\lceil\frac{n}{k}\rceil - 1$$$ segments remaining. If there is one more element having value equal to $$$\lceil\frac{n}{k}\rceil$$$, we won't be able to place that element without violating the condition. There are less segments and more values, then by the Pigeon-Hole principle, there will be two values in the same segment(box). The distance between these two same values will be less than $$$k$$$.
Actually placing the first $$$K'$$$ elements having value equal to $$$\lceil\frac{n}{k}\rceil$$$ in the $$$last$$$ segment and then cyclically placing them in the next segments is the only way.
Proof: Note that right now we are only dealing with those elements having value equal to $$$\lceil\frac{n}{k}\rceil$$$.
Let's increase the distance between any two same elements (Let's call them $$$A$$$) in any consecutive segment by $$$x$$$. The new distance is $$$k+x$$$. Then the distance between the element $$$A$$$ in the next segment and the current segment decreases by $$$x$$$ making it $$$k-x$$$. To accommodate this change, the $$$A$$$ in the next segment will have to be moved by at least $$$x$$$. This creates a chain reaction that will reach the last segment. Since the size of the last segment is less than or equal to $$$k$$$, then $$$A$$$ in the last segment will have nowhere to move. So we can say that placing the element in the last segment decides the order in the next subsequent segments.
Sometimes "chain" reaction would be resolvable, but you phase it like it will always fail: example:
Please, stop claim you know proof when you don't. It obstruct comments section.
You wanted an explanation of the case when frequency of values equal to $$$\lceil\frac{n}{k}\rceil$$$ exceeds the remainder. I gave an explanation for that.
Why are you giving a rebuttal with an invalid test case?
Because I don't see why similar thing may not happen. If you're talking about case which is you claim is impossible, then starting from some arrangement and then extending distance is odd idea. Because if it's already impossible, why then we extend distance. If it's possible, then claim is wrong. If you consider some unfinished filling, with empty spots, then you just may consider my example with all colors > 2 not yet filled:
Why I send this example, because this "chain" of reactions is perfectly fine, because one color just jumps to the front (but you claim it should only move farther, I'm extending distance between two cells of color 2)
Then why in your first reply to my question not just say "we can't place a1 in first places of all segments because we can't place $$$a_3$$$ then". It's not a proof if you tried all possibilities for some example and it didn't work.
Claim without reasoning. Many other statements also without reasoning.
I came up with proof of first claim myself. Here it is.
Consider case when $$$n$$$ divisible by $$$k$$$. If we split into boxes by $$$k$$$, then we have $$$\frac{n}{k}$$$ boxes, each of size $$$\leq k$$$. This means, that in one box there can not be two elements of same color (by requirement from the statement). So, in box can be 0 or 1 occurrences of a color. Then, there can not be more than $$$k$$$ of colors with $$$a_i = \frac{n}{k}$$$. Proof by contradiction. Suppose $$$c$$$ is the number of colors with $$$a_i = \frac{n}{k}$$$ and $$$c > k$$$. Then number of colors $$$c$$$ times their number $$$\frac{n}{k}$$$ will be $$$c \times \frac{n}{k}$$$ which is greater than $$$k \times \frac{n}{k} = n$$$. So, total number of such $$$a_i$$$ is bigger than $$$n$$$, this is contradiction with requirement that sum of $$$a_i$$$ is equal to $$$n$$$.
Consider case when $$$n$$$ is not divisible by $$$k$$$. Let $$$r = n \bmod k$$$. Then, there is $$$\left\lceil\frac{n}{k}\right\rceil$$$ boxes, and last box with $$$r$$$ elements. Similarly, there can not be more than one occurrence of color within box of size $$$k$$$. Also, easy to show that there can not be two elements of same color in last box of size $$$r$$$. Then for each box, the number of occurrences of a color can be 0 or 1. Then, for color with $$$a_i = \left\lceil\frac{n}{k}\right\rceil$$$ it will have occurrence 1 in all boxes! Then, the number of colors like that can not be $$$> r$$$. Proof by contradiction. Suppose $$$c$$$ is the number of colors with $$$a_i = \left\lceil\frac{n}{k}\right\rceil$$$ and $$$c > r$$$. Then, each of colors like that, should have occurrence 1 in all boxes, in particular: in last box! This means, last box should have $$$c$$$ colors, but $$$c > r$$$. Contradiction with capacity of last box.
Please add a test case with t=1; n=2; m=500000 in Problem D. the First array with all 1's and 2nd array with all 0's. I have seen many solutions with M^2 in solution getting accepted. Please look into it. 185717356
In fact, you can hack it. However, I have hacked it.
Thank you for providing the test.
My unproven solution to G:
We must start with an interval with $$$x=l$$$. Choosing an interval with the highest $$$y$$$ is irrelevant because whether you choose one with lower $$$y$$$ or not is pointless so the sum is $$$0$$$ so we can ignore it; that repeats until you get to the interval with lowest $$$y$$$, let's call that lowest $$$y$$$ $$$e_1$$$. Now the new intervals are the ones with $$$x$$$ in $$$[l+1,e_1]$$$; once again we find the interval with the lowest $$$y$$$ out of the ones which have $$$x$$$ in $$$[l+1,e_1]$$$, call that lowest $$$y$$$ $$$e_2$$$, continue the process with $$$[e_1+1,e_2]$$$, etc. until $$$e_i=r$$$ or we see that that's impossible, if it's impossible then the answer is 0, otherwise whether it's $$$1$$$ or $$$-1$$$ depends on the length of the path.
I precompute all the intervals which are possible to reach using this process and use binary lifting to answer queries. Code: 185786867.
The unproven part is the complexity; I don't know how many intervals are possible to reach using this process. It's not hard to see that the sum of lengths of intervals is $$$O(n^2)$$$, which means that there can be at most $$$O(n\sqrt{n})$$$ of them. Is there a better upper bound on the amount of reachable intervals?
The solution for G is a bit strange.
This is not true. For eg. if the segments are $$$[1,3],[4,6],[2,5],[3,4]$$$ and $$$[l,r]$$$ is $$$[1,6]$$$, then the answer is equal to $$$1$$$ (not zero) and also $$$[2,5]$$$ contains the segment $$$[3,4]$$$.
Why did you reply to my comment? Your reply is completely irrelevant to my comment.
I recommend reading the part of the editorial that you quoted more carefully. It just says that the solution will stay the same if we delete $$$[2,5]$$$, not that the solution is 0 due to its existence.
Totally blown away by the knapsack trick in F2 of the array where $$$2a_{i-1} \lt a_{i}$$$. Is it a well-known trick among high rated contestants, or is it something ad-hoc for this problem?
Tagging the author of the Problem Little09
In my opinion, some high rated contestants might have seen it in other problems. However, when I made this problem, I was unfamiliar with the trick. But I think it is not difficult to solve it after observing $$$a_i>\sum_{j=1}^{i-1}a_j$$$.
https://mirror.codeforces.com/contest/1774/submission/185708026 Can anyone help me, why is my submission wrong?
Take a look at Ticket 16646 from CF Stress for a counter example.
ooohhh I understandd. Thank you so much.
Can anyone tell what's wrong in my approach for Problem-E, 189112092 its failing at test 20...
My approach: I am first calculating minimum number of steps separately for the two chess pieces. For each piece, for a particular node, if there exists a node in its subtrees (or the node itself) which is supposed to be travelled(is in the piece's sequence), then increase the number of steps by 2 as we will have to reach the root node of that subtree atleast once. This path of nodes is marked(coloured) separately for both nodes. At the end, subtract 2 from steps as the piece was already there on the root of the whole tree.
Then I am calculating the extra steps separately for each piece that they will have to travel. For each piece, at a particular node which has to be traversed atleast once, if the other piece's marked path's distance becomes more than 'd' (given in ques), then increase number of steps by 2, as we will have to pull down the other piece atleast one node down.
Easy Solution for Problem E with Neat code
In problem C, lets consider x = 3 in the first test case
string = 0 0 1
array = 1 2 3 4
It is already mentioned in the notes section that player 2, 3 and 4 can win this round, but what about player 1?
condition for 1 to win: 4 beats 2 (ground 1), 3 beats 4 (ground 0) and 1 beats 3 (ground 0)
Is this not right?