1770A - Koxia and Whiteboards
Idea by m_99
Exactly $$$n$$$ items out of of $$$a_1,\ldots,a_n,b_1,\ldots,b_m$$$ will remain on the whiteboard at the end.
$$$b_m$$$ will always remain on the board at the end.
Consider the case where $$$n=2$$$ and $$$m=2$$$. As we mentioned in hint 2, $$$b_2$$$ will always be written, but what about $$$b_1$$$?
This problem can be solved naturally with a greedy algorithm — for $$$i = 1, 2, \dots, m$$$, we use $$$b_i$$$ to replace the minimal value among the current $$$a_1, a_2, \dots, a_n$$$. The time complexity is $$$O(nm)$$$ for each test case.
Alternatively, we can first add $$$b_m$$$ to our final sum. For the remaining $$$(n+m-1)$$$ integers, we can freely pick $$$(n - 1)$$$ out of them and add it to our final sum. This is because if we want a certain $$$a_i$$$ to remain on the board at the end, we simply do not touch it in the process. If we want a certain $$$b_i$$$ to remain on the board at the end, then on the $$$i^{th}$$$ operation we replace some $$$a_j$$$ that we do not want at the end by $$$b_i$$$.
Using an efficient sorting algorithm gives us a $$$O((n + m) \log (n + m))$$$ solution, which is our intended solution.
#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for (int i = 0; i < (n); ++i)
#define Inf32 1000000001
#define Inf64 4000000000000000001
int main(){
int _t;
cin>>_t;
rep(_,_t){
int n,m;
cin>>n>>m;
vector<long long> a(n+m);
rep(i,n+m)scanf("%lld",&a[i]);
sort(a.begin(),a.end()-1);
reverse(a.begin(),a.end());
long long ans = 0;
rep(i,n)ans += a[i];
cout<<ans<<endl;
}
return 0;
}
1770B - Koxia and Permutation
Idea by m_99
For $$$k = 1$$$, the cost is always $$$2n$$$ for any permutation.
For $$$k \geq 2$$$, the minimal cost is always $$$n + 1$$$.
When $$$k = 1$$$ every permutation has the same cost.
When $$$k \geq 2$$$, the minimal cost will be at least $$$n+1$$$. This is because there will always be at least one segment containing the element $$$n$$$ in the permutation, contributing $$$n$$$ to the "max" part of the sum, and the "min" part will add at least $$$1$$$ to the sum.
In fact, the cost $$$n+1$$$ is optimal. It can be achieved by ordering the numbers in the pattern $$$[n, 1, n - 1, 2, n - 2, 3, n - 3, 4, \dots]$$$.
The time complexity is $$$O(n)$$$ for each test case. Other careful constructions should also get Accepted.
#include <iostream>
#define MULTI int _T; cin >> _T; while(_T--)
using namespace std;
typedef long long ll;
int n, k;
int main () {
ios::sync_with_stdio(0);
cin.tie(0);
MULTI {
cin >> n >> k;
int l = 1, r = n, _ = 1;
while (l <= r) cout << ((_ ^= 1) ? l++ : r--) << ' ';
cout << endl;
}
}
1770C - Koxia and Number Theory
Idea by triple__a
If $$$a_i$$$ are not pairwise distinct we get a trivial NO.
If all $$$a_i$$$ are pairwise distinct, can you construct an example with $$$n = 4$$$ that gives an answer NO?
Perhaps you are thinking about properties such as parity? Try to generalize the idea.
Consider every prime. Consider Chinese Remainder Theorem.
How many primes should we check? Consider Pigeonhole Principle.
First, we should check whether the integers in $$$a$$$ are pairwise distinct, as $$$a_i + x \geq 2$$$ and $$$\gcd(t,t)=t$$$, which leads to a trivial NO.
Given an integer $$$x$$$, let's define $$$b_i := a_i + x$$$. The condition "$$$\gcd(b_i,b_j)=1$$$ for $$$1\le i < j \le n$$$" is equivalent to "every prime $$$p$$$ should divides at most one $$$b_i$$$". Given a prime $$$p$$$, how should we verify whether for every $$$x > 0$$$, $$$p$$$ divides at least two elements in $$$b$$$?
A small but guided sample is $$$a = [5, 6, 7, 8]$$$ with answer NO, because
- $$$\gcd(6 + x, 8 + x) \neq 1$$$ if $$$x \equiv 0 \pmod 2$$$,
- $$$\gcd(5 + x, 7 + x) \neq 1$$$ if $$$x \equiv 1 \pmod 2$$$.
That is, if we consider $$$[5, 6, 7, 8]$$$ modulo $$$2$$$, we obtain the multiset $$${1, 0, 1, 0}$$$. Both $$$0$$$ and $$$1$$$ appeared twice, so for any choice of $$$x$$$, exactly two integers in $$$b$$$ will be divided by $$$2$$$.
This idea can be extended to larger primes. For a given prime $$$p$$$, let $$$cnt_j$$$ be the multiplicity of $$$j$$$ in the multiset $$$[ a_i \text{ mod } p, a_2 \text{ mod } p, \dots, a_n \text{ mod } p ]$$$. If $$$\min(\mathit{cnt}_0, \mathit{cnt}_1, \dots, \mathit{cnt}_{p-1}) \geq 2$$$, we output NO immediately.
While there are many primes up to $$${10}^{18}$$$, we only need to check for the primes up to $$$\lfloor \frac{n}{2} \rfloor$$$. This is because $$$\min(\mathit{cnt}_0, \mathit{cnt}_1, \dots, \mathit{cnt}_{p-1}) \geq 2$$$ is impossible for greater primes according to Pigeonhole Principle. Since the number of primes up to $$$\lfloor \frac{n}{2} \rfloor$$$ is at most $$$O\left(\frac{n}{\log n} \right)$$$, the problem can be solved in time $$$O\left(\frac{n^2}{\log n} \right)$$$.
The reason that $$$\min(\mathit{cnt}) \geq 2$$$ is essential because for a prime $$$p$$$, if $$$a_u \equiv a_v \pmod p$$$, then it's necessary to have $$$(x + a_u) \not\equiv 0 \pmod p$$$, because $$$\gcd(x + a_u, x + a_v)$$$ will be divided by $$$p$$$ otherwise. So actually, $$$\mathit{cnt}_i \geq 2$$$ means $$$x \not\equiv (p-i) \pmod p$$$. If $$$\min(\mathit{cnt}) < 2$$$ holds for all primes, then we can list certain congruence equations and use Chinese Reminder Theorem to calculate a proper $$$x$$$; if there exists a prime that $$$\min(\mathit{cnt}) \geq 2$$$, then any choose of $$$x$$$ leads to the situation that $$$p$$$ appears twice.
#include <iostream>
#include <algorithm>
#define MULTI int _T; cin >> _T; while(_T--)
using namespace std;
typedef long long ll;
const int N = 105;
const int INF = 0x3f3f3f3f;
template <typename T> bool chkmin (T &x, T y) {return y < x ? x = y, 1 : 0;}
template <typename T> bool chkmax (T &x, T y) {return y > x ? x = y, 1 : 0;}
int n;
ll a[N];
int cnt[N];
int main () {
ios::sync_with_stdio(0);
cin.tie(0);
MULTI {
cin >> n;
for (int i = 1;i <= n;++i) {
cin >> a[i];
}
int isDistinct = 1;
sort(a + 1, a + n + 1);
for (int i = 1;i <= n - 1;++i) {
if (a[i] == a[i + 1]) isDistinct = 0;
}
if (isDistinct == 0) {
cout << "NO" << endl;
continue;
}
int CRT_able = 1;
for (int mod = 2;mod <= n / 2;++mod) {
fill(cnt, cnt + mod, 0);
for (int i = 1;i <= n;++i) {
cnt[a[i] % mod]++;
}
if (*min_element(cnt, cnt + mod) >= 2) CRT_able = 0;
}
cout << (CRT_able ? "YES" : "NO") << endl;
}
}
1770D - Koxia and Game
Idea by m_99
If all of $$$a$$$, $$$b$$$ and $$$c$$$ are fixed, how to determine who will win?
If $$$a$$$ and $$$b$$$ are fixed, design an algorithm to check if there is an array $$$c$$$ that makes Koxia wins.
If you can't solve the problem in Hint 2, try to think about how it's related to graph theory.
Try to discuss the structure of components in the graph to count up the number of $$$c$$$.
Firstly, let's consider how an array $$$c$$$ could make Koxia wins.
Lemma 1. In each round, Koxia should remove an element in $$$S$$$ to make the remaining $$$2$$$ elements in $$$S$$$ the same (i.e. Mahiru's choice determined nothing actually).
- In round $$$n$$$, if Koxia leaves two choices for Mahiru then Mahiru will be able to prevent $$$d$$$ from being a permutation.
- This means if Koxia wins, there is only one choice for $$$d_n$$$.
- Now $$$(d_1, d_2, \dots, d_{n-1})$$$ have to be a permutation of a specific $$$n-1$$$ numbers. Apply the same argument on $$$d_{n-1}$$$ and so on, we can conclude that every $$$d_i$$$ only has one choice if Koxia wins.
Lemma 2. Let $$$p$$$ be array of length $$$n$$$ where we can set $$$p_i$$$ to either $$$a_i$$$ or $$$b_i$$$. Koxia wins iff there exists a way to make $$$p$$$ a permutation.
- According to Lemma 1, if there is a way to make $$$p$$$ a permutation, we can just set $$$c_i = p_i$$$. Koxia can then force Mahiru to set $$$d_i = p_i$$$ every round and Koxia will win.
- If it is impossible to make $$$p$$$ a permutation, Mahiru can pick either $$$a_i$$$ or $$$b_i$$$ (at least one of them is available) every round. The resulting array $$$d$$$ is guaranteed to not be a permutation.
First, we need an algorithm to determine if there is a way to make $$$p$$$ a permutation.
We can transform this into a graph problem where $$$(a_i, b_i)$$$ are edges in a graph with $$$n$$$ vertices. Then there is a way to make $$$p$$$ a permutation iff there is a way to assign a direction for every edge such that every vertex has one edge leading into it. It is not hard to see that this is equivalent to the condition that for every connected component, the number of edges equals the number of vertices. We can verify this by a Disjoint-Set Union or a graph traversal in $$$O(n \alpha(n))$$$ or $$$O(n)$$$ time complexity.
To solve the counting problem, we consider the structure of the connected components one by one. A component with $$$|V| = |E|$$$ can be viewed as a tree with an additional edge. This additional edge can be categorized into two cases:
- The additional edge forms a cycle together with some of the other edges. There are $$$2$$$ choices for the cycle (clockwise and counterclockwise), and the choices of other edges are fixed then (point away from the cycle).
- The additional edge forms a self-loop. Then the value of $$$c_i$$$ determines nothing in this situation so it can be any integers in $$$[1, n]$$$, and the choices of all other edges are fixed.
Therefore, if exists at least one $$$c$$$ to make Koxia wins, then the answer is $$$2^{\textrm{cycle component cnt}} \cdot n^{\textrm{self-loop component cnt}}$$$. The time complexity is $$$O(n \alpha(n))$$$ or $$$O(n)$$$.
#include <iostream>
#include <numeric>
#define MULTI int _T; cin >> _T; while(_T--)
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
const int mod = 998244353;
int n;
int a[N], b[N];
int fa[N], cnt_v[N], cnt_e[N], selfloop[N];
int vis[N];
void init () {
iota(fa + 1, fa + n + 1, 1);
fill(cnt_v + 1, cnt_v + n + 1, 1);
fill(cnt_e + 1, cnt_e + n + 1, 0);
fill(selfloop + 1, selfloop + n + 1, 0);
fill(vis + 1, vis + n + 1, 0);
}
int getfa (int x) {
return fa[x] == x ? x : fa[x] = getfa(fa[x]);
}
void merge (int u, int v) {
u = getfa(u);
v = getfa(v);
cnt_v[u] += cnt_v[v];
cnt_e[u] += cnt_e[v];
selfloop[u] |= selfloop[v];
fa[v] = u;
}
int main () {
ios::sync_with_stdio(0);
cin.tie(0);
MULTI {
cin >> n;
for (int i = 1;i <= n;++i) {
cin >> a[i];
}
for (int i = 1;i <= n;++i) {
cin >> b[i];
}
init();
for (int i = 1;i <= n;++i) {
if (getfa(a[i]) != getfa(b[i])) merge(a[i], b[i]);
cnt_e[getfa(a[i])]++;
if (a[i] == b[i]) selfloop[getfa(a[i])] = 1;
}
ll ans = 1;
for (int i = 1;i <= n;++i) if (vis[getfa(i)] == 0) {
if (cnt_v[getfa(i)] != cnt_e[getfa(i)]) ans = 0;
else ans = ans * (selfloop[getfa(i)] ? n : 2) % mod;
vis[getfa(i)] = 1;
}
cout << ans << endl;
}
}
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int P = 998244353;
int n, a[N], b[N];
vector <int> G[N];
bool vis[N];
int vertex, edge, self_loop;
void dfs(int x) {
if (vis[x]) return ;
vis[x] = true;
vertex++;
for (auto y : G[x]) {
edge++;
dfs(y);
if (y == x) {
self_loop++;
}
}
}
void solve() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i++) scanf("%d", &b[i]);
for (int i = 1; i <= n; i++) G[i].clear();
for (int i = 1; i <= n; i++) {
G[a[i]].push_back(b[i]);
G[b[i]].push_back(a[i]);
}
int ans = 1;
for (int i = 1; i <= n; i++) vis[i] = false;
for (int i = 1; i <= n; i++) {
if (vis[i]) continue ;
vertex = 0;
edge = 0;
self_loop = 0;
dfs(i);
if (edge != 2 * vertex) {
ans = 0;
} else if (self_loop) {
ans = 1ll * ans * n % P;
} else {
ans = ans * 2 % P;
}
}
printf("%d\n", ans);
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
solve();
}
return 0;
}
1770E - Koxia and Tree
Idea by m_99
Solve a classic problem — find the sum of pairwise distances of $$$k$$$ chosen nodes in a tree.
If we add the move operations while the direction of edges are fixed, find the sum of pairwise distances of $$$k$$$ chosen nodes.
If you can't solve the problem in Hint 2, consider why writers make each edge passed by butterflies for at most once.
When the direction of edges become random, how maintaining $$$p_i$$$ as the possibility of "node $$$i$$$ contains a butterfly" help you to get the answer?
At first sight, we usually think of a classic problem — find the sum of pairwise distances of $$$k$$$ chosen nodes in a tree. For any edge, if there are $$$x$$$ chosen nodes and $$$n - x$$$ chosen nodes respectively on each side of it, then there will be $$$x (n - x)$$$ pairs of nodes passing this edge. Without loss of generality, let's assign node $$$1$$$ as root, and define both $$$\mathit{siz}_i$$$ as the number of chosen nodes in subtree $$$i$$$. By summing up $$$\mathit{siz}_{\mathit{son}} (n - \mathit{siz}_{\mathit{son}})$$$ for each edge $$$(\mathit{fa}, \mathit{son})$$$, we derive the answer, which equals to the expected value of the distance of two nodes (Uniformly randomly chosen from $$$k$$$ nodes) after dividing by $$$\binom{k}{2}$$$.
Let's turn to Hint 2 then — add the move operations while the direction of edges are fixed. Let's define $$$\mathit{siz}^0_i$$$ and $$$\mathit{siz}_i$$$ as the number of butterflies in subtree $$$i$$$, but before any move operation / in real time respectively. A very important observation is, although butterflies are moving, we can always claim $$$|\mathit{siz}_{\mathit{son}} - \mathit{siz}^0_{\mathit{son}}| \leq 1$$$ because each edge is passed by butterflies for at most once. This property allows us to discuss different values of $$$\mathit{siz}_{\mathit{son}}$$$ to sum up the answer in constant time complexity, if you maintain butterflies' positions correctly.
When we introduce random directions additionally, if we define $$$p_i$$$ as the possibility of "node $$$i$$$ contains a butterfly", then an equivalent statement of move operation from node $$$u$$$ to node $$$v$$$ will be, actually, set $$$p_u = p_v = \frac{p_u+p_v}{2}$$$, which allows us to maintain $$$p$$$ in real time easily. Similarly, by discussing values of $$$\mathit{siz}_{\mathit{son}}$$$ (but with possibilities of each case instead of specified moves), we get the final answer. The total time complexity is $$$O(n)$$$.
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 3e5 + 5;
const int mod = 998244353;
const int inv2 = 499122177;
ll qpow (ll n, ll m) {
ll ret = 1;
while (m) {
if (m & 1) ret = ret * n % mod;
n = n * n % mod;
m >>= 1;
}
return ret;
}
ll getinv (ll a) {
return qpow(a, mod - 2);
}
int n, k;
int a[N];
int u[N], v[N];
vector <int> e[N];
int fa[N];
ll p[N], sum[N];
void dfs (int u, int f) {
sum[u] = p[u];
for (int v : e[u]) if (v != f) {
dfs(v, u);
fa[v] = u;
sum[u] += sum[v];
}
}
int main () {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> k;
for (int i = 1;i <= k;++i) {
cin >> a[i];
p[a[i]] = 1;
}
for (int i = 1;i <= n - 1;++i) {
cin >> u[i] >> v[i];
e[u[i]].push_back(v[i]);
e[v[i]].push_back(u[i]);
}
dfs(1, -1);
ll ans = 0;
for (int i = 1;i <= n - 1;++i) {
if (fa[u[i]] == v[i]) swap(u[i], v[i]);
ll puv = p[u[i]] * (1 - p[v[i]] + mod) % mod;
ll pvu = p[v[i]] * (1 - p[u[i]] + mod) % mod;
ll delta = 0;
delta -= puv * sum[v[i]] % mod * (k - sum[v[i]]) % mod;
delta -= pvu * sum[v[i]] % mod * (k - sum[v[i]]) % mod;
delta += puv * (sum[v[i]] + 1) % mod * (k - sum[v[i]] - 1) % mod;
delta += pvu * (sum[v[i]] - 1) % mod * (k - sum[v[i]] + 1) % mod;
ans = (ans + sum[v[i]] * (k - sum[v[i]]) + delta * inv2) % mod;
ans = (ans % mod + mod) % mod;
p[u[i]] = p[v[i]] = 1ll * (p[u[i]] + p[v[i]]) * inv2 % mod;
}
cout << ans * getinv(1ll * k * (k - 1) / 2 % mod) % mod << endl;
}
1770F - Koxia and Sequence
Idea by m_99
From symmetry, for any non-negative integer $$$t$$$, the number of good sequences with $$$a_1=t$$$, the number of good sequences with $$$a_2=t$$$, ... are equal.
It is useful to consider the contribution of each bit to the answer independently.
Since XOR is undone twice, considering the contribution to the answer can be regarded as counting up over mod $$$2$$$.
It is difficult to count those for which total or is $$$y$$$, but it is relatively easy to count those for which total or is a subset of $$$y$$$. Then, we can consider a way using the inclusion-exclusion principle.
Lucas's theorem and Kummer's theorem are useful. In particular, you can derive equivalence conditions on or.
"There are $$$a+b$$$ white balls. For every pair $$$(c,d)$$$ of nonnegative integers satisfying $$$c+d=n$$$, find the sum of the ways to choose $$$c$$$ balls from the first $$$a$$$ balls and $$$d$$$ balls from the remaining $$$b$$$ balls." The answer to this problem is $$$_{a+b} C_{n}$$$. This is because considering how to choose for every pair $$$(c,d)$$$ of non-negative integers satisfying $$$c+d=n$$$ merely consider the case of choosing $$$n$$$ balls as how many balls to choose from $$$a$$$ balls and $$$b$$$ balls. This result is called Vandermonde's identity.
Let $$$f(i,t)$$$ is the number of good sequence such that $$$a_i=t$$$. $$$f(1,t)=f(2,t)=...=f(n,t)$$$, so if $$$n$$$ is even, the answer is $$$0$$$. Otherwise, the answer is total xor of $$$t$$$ such that number of good sequences such that $$$a_1=t$$$ is odd. We can consider each bit independently, so we can rewrite the problem "for each $$$i$$$, find the number of good sequences such that $$$a_1$$$'s $$$i$$$-th bit is $$$1$$$, modulo $$$2$$$".
Let $$$g(y')$$$ is the answer if $$$y$$$ is a subset of $$$y'$$$(means $$$y \mid y'=y'$$$). We can prove with induction the answer of the original problem is total xor of $$$g(y')$$$ such that $$$y'$$$ is a subset of given $$$y$$$. So, the goal is for each $$$i$$$, find the number of $$$y'$$$ such that $$$y'$$$ is a subset of $$$y$$$ and $$$g(y')$$$'s $$$i$$$-th bit is $$$1$$$, modulo $$$2$$$.
We can prove with Lucas's theorem or Kummer's theorem ($$$p=2$$$), "$$$\binom{a}{b} \bmod 2$$$ is $$$1$$$" is equivalent to "$$$b$$$ is a subset of $$$a$$$". The number of sequences such that the length is $$$n$$$ and total sum is $$$x$$$ and total or is a subset of $$$y$$$, modulo $$$2$$$ is equal to $$$\sum_{t_1+\ldots+t_n=x} \prod{} \binom{y}{t_i}$$$, because if there is $$$t_i$$$ which is not a subset of $$$y$$$, $$$\binom{y}{t_i}$$$ is $$$0$$$ and the product is also $$$0$$$, modulo $$$2$$$. Consider Vandermonde's identity, the value is equal to $$$\binom{ny}{x}$$$. In a similar way, we can rewrite the problem to "for each $$$i$$$, find the number of $$$y'$$$ such that $$$y'$$$ is a subset of $$$y$$$ and $$$y'$$$'s $$$i$$$-th bit is $$$1$$$ and $$$x-2^i$$$ is a subset of $$$ny'-2^i$$$($$$\binom{ny'-2^i}{x-2^i} \bmod 2 = 1$$$), modulo $$$2$$$".
From the above, we can solve this problem in $$$O(y \log y)$$$ by performing the calculation in $$$O(1)$$$ for all $$$i$$$ and all $$$y'$$$.
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n,a,b;
bool isSub(int i,int j){
if (i<0 || j<0) return false;
return (j&i)==i;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n>>a>>b;
int ans=0;
for (int sub=b;sub;sub=(sub-1)&b) rep(bit,0,20) if (sub&(1<<bit)){
if (isSub(a-(1<<bit),n*sub-(1<<bit))){
ans^=(1<<bit);
}
}
cout<<ans*(n%2)<<endl;
}
1770G - Koxia and Bracket
Idea by huangxiaohua and errorgorn
What special properties does the deleted bracket sequence have?
Try to solve this with $$$O(n^2)$$$ DP.
If there is no balance requirement, can multiple brackets be processed quickly with one operation?
Can you combine the last idea with divide-and-conquer or something?
$$$O(n^2)$$$ Solution
Let us consider what properties the removed bracket subsequence has.
First, it must be a bracket subsequence in the form ))...)((....(. The proof is simple: if there is a deleted ) on the right-hand side of a (, then we can keep them in $$$s$$$ without breaking the balancing property of the remaining sequence.
This property means that we can divide the string into $$$2$$$ parts. We only delete ) from the first part and only delete ( from the second part. Now let us try to find the dividing point between the two parts: Consider a prefix sum based on a sequence of brackets in which each ( is replaced by 1 and each ) is replaced by -1.
We define a position as a special position if and only if the number corresponding to this position is less than the previously occurring minimum value. It is easy to see that whenever a special position occurs, we must remove an additional ) before this position to make the bracket sequence satisfy the condition again.
Considering the above idea, we can find that only the ) before the farthest special position may be deleted, so we can use this position as the dividing point.
We now solve two separate problems. However, we can turn the problem on deleting only '(' into the one on deleting only ). For example, if we are only allowed to delete ( from (()((()()), it is equivalent to the number of ways to delete only ) from (()()))()).
For the part where only ) is deleted, the sufficient condition for it to be a balanced bracket sequence is that each number in the prefix sum must be greater than 0 after the operation.
Also considering the above ideas, let us define the state $$$dp_{i,j}$$$, which represents after removing the breakets required by special position, the number of ways to delete additional $$$j$$$ $$$(j \geq 0)$$$ occurrence of ) from the string up the $$$i$$$-th occurrence of ) in the string.
Multiply the $$$dp_{end,0}$$$ obtained from both parts of the string to obtain the answer. The time complexity is $$$O(n^2)$$$ and optimized implementations can run in about 9 seconds, but it is not enough to pass.
$$$O(n\sqrt{n \log n})$$$ Solution
Let's try to optimize the transitions when there are no special positions. For state $$$dp_{i,j}$$$, after processing $$$k$$$ individual ), the transitions are as follows:
We find that this transfer equation behaves as a polynomial convolution. Thus we can optimize this convolution by NTT with a time complexity of $$$O(n \log n)$$$ for a single operation, while the worst global complexity of this Solution is $$$O(n^2 \log n)$$$ due to the presence of the special position.
Consider how this Solution can be combined with the $$$O(n^2)$$$ Solution. For states $$$dp_{i,j}$$$ where we want to consider its contribution to $$$dp_{i+k}$$$, if $$$j \geq k$$$ is satisfied, then the transitions are not affected by the special position anyway.
Based on the above idea, we can adopt a mixed Solution based on periodic reconstruction: set the reconstruction period $$$B$$$, and within one round of the period, we use the $$$O(n^2)$$$ DP Solution to handle the part of $$$j \le B$$$, while for the part of $$$j>B$$$, we compute the answer by NTT after one round of the period.
The time complexity $$$O(\frac{n^2}{B}+B\cdot n \log n)$$$ can be optimized to $$$O(n\sqrt{n \log n})$$$ by setting the appropriate $$$B$$$. Although the time complexity is still high, given the low constant factor of the $$$O(n^2)$$$ solution, a decently-optimized implementation is able to get AC.
$$$O(n\log^2 n)$$$ Solution
Consider combining the idea of extracting $$$j \geq k$$$ parts for NTT with divide-and-conquer. Suppose now that the interval to be processed is $$$(l,r)$$$, where the DP polynomial passed is $$$s$$$. We proceed as follows:
- Count the number of special positions $$$num$$$ in the interval $$$(l,r)$$$, extract the part of the polynomial $$$s$$$ corresponding to the state $$$j \geq num$$$, and convolute it with the current interval alone.
- Pass the part of the polynomial $$$s$$$ corresponding to the state $$$j < num$$$ into the interval $$$(l,mid)$$$, and then pass the result into the interval $$$(mid+1,r)$$$ to continue the operation.
- Add the polynomials obtained by the above two steps directly, and return the obtained polynomial.
How to calculate the time complexity of performing the above operations? Let's analyze the operations passed into the left interval and the right interval separately.
- When passing in the left interval $$$(l,mid)$$$, the size of the polynomial for the NTT operation is the number of special positions in the interval $$$(l,r)$$$ minus the number of special positions in the left interval $$$(l,mid)$$$, i.e., the number of special positions in the right interval $$$(mid+1,r)$$$, which does not exceed the length of the right interval $$$(mid+1,r)$$$.
- When passed into the right interval $$$(mid+1,r)$$$, the size of the polynomial does not exceed the length of the left interval $$$(l,mid)$$$.
- Also, the length of the combinatorial polynomial multiplied with $$$s$$$ is the interval length + 1.
In summary, the size of the two polynomials for the NTT operation in the interval $$$(l,r)$$$ does not exceed the interval length + 1. Thus the time complexity of this solution is divide-and-conquer combined with the time complexity of NTT, i.e. $$$O(n \log^2 n)$$$.
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define int long long
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
const int MOD=998244353;
ll qexp(ll b,ll p,int m){
ll res=1;
while (p){
if (p&1) res=(res*b)%m;
b=(b*b)%m;
p>>=1;
}
return res;
}
ll inv(ll i){
return qexp(i,MOD-2,MOD);
}
ll fix(ll i){
i%=MOD;
if (i<0) i+=MOD;
return i;
}
ll fac[1000005];
ll ifac[1000005];
ll nCk(int i,int j){
if (i<j) return 0;
return fac[i]*ifac[j]%MOD*ifac[i-j]%MOD;
}
//https://github.com/kth-competitive-programming/kactl/blob/main/content/numerical/NumberTheoreticTransform.h
const ll mod = (119 << 23) + 1, root = 62; // = 998244353
// For p < 2^30 there is also e.g. 5 << 25, 7 << 26, 479 << 21
// and 483 << 21 (same root). The last two are > 10^9.
typedef vector<int> vi;
typedef vector<ll> vl;
void ntt(vl &a) {
int n = sz(a), L = 31 - __builtin_clz(n);
static vl rt(2, 1);
for (static int k = 2, s = 2; k < n; k *= 2, s++) {
rt.resize(n);
ll z[] = {1, qexp(root, mod >> s, mod)};
rep(i,k,2*k) rt[i] = rt[i / 2] * z[i & 1] % mod;
}
vi rev(n);
rep(i,0,n) rev[i] = (rev[i / 2] | (i & 1) << L) / 2;
rep(i,0,n) if (i < rev[i]) swap(a[i], a[rev[i]]);
for (int k = 1; k < n; k *= 2)
for (int i = 0; i < n; i += 2 * k) rep(j,0,k) {
ll z = rt[j + k] * a[i + j + k] % mod, &ai = a[i + j];
a[i + j + k] = ai - z + (z > ai ? mod : 0);
ai += (ai + z >= mod ? z - mod : z);
}
}
vl conv(const vl &a, const vl &b) {
if (a.empty() || b.empty()) return {};
int s = sz(a) + sz(b) - 1, B = 32 - __builtin_clz(s), n = 1 << B;
int inv = qexp(n, mod - 2, mod);
vl L(a), R(b), out(n);
L.resize(n), R.resize(n);
ntt(L), ntt(R);
rep(i,0,n) out[-i & (n - 1)] = (ll)L[i] * R[i] % mod * inv % mod;
ntt(out);
return {out.begin(), out.begin() + s};
}
vector<int> v;
vector<int> solve(int l,int r,vector<int> poly){
if (poly.empty()) return poly;
if (l==r){
poly=conv(poly,{1,1});
poly.erase(poly.begin(),poly.begin()+v[l]);
return poly;
}
int m=l+r>>1;
int num=0;
rep(x,l,r+1) num+=v[x];
num=min(num,sz(poly));
vector<int> small(poly.begin(),poly.begin()+num);
poly.erase(poly.begin(),poly.begin()+num);
vector<int> mul;
rep(x,0,r-l+2) mul.pub(nCk(r-l+1,x));
poly=conv(poly,mul);
small=solve(m+1,r,solve(l,m,small));
poly.resize(max(sz(poly),sz(small)));
rep(x,0,sz(small)) poly[x]=(poly[x]+small[x])%MOD;
return poly;
}
int solve(string s){
if (s=="") return 1;
v.clear();
int mn=0,curr=0;
for (auto it:s){
if (it=='(') curr++;
else{
curr--;
if (curr<mn){
mn=curr;
v.pub(1);
}
else{
v.pub(0);
}
}
}
return solve(0,sz(v)-1,{1})[0];
}
int n;
string s;
int pref[500005];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
fac[0]=1;
rep(x,1,1000005) fac[x]=fac[x-1]*x%MOD;
ifac[1000004]=inv(fac[1000004]);
rep(x,1000005,1) ifac[x-1]=ifac[x]*x%MOD;
cin>>s;
n=sz(s);
pref[0]=0;
rep(x,0,n) pref[x+1]=pref[x]+(s[x]=='('?1:-1);
int pos=min_element(pref,pref+n+1)-pref;
string a=s.substr(0,pos),b=s.substr(pos,n-pos);
reverse(all(b)); for (auto &it:b) it^=1;
cout<<solve(a)*solve(b)%MOD<<endl;
}
1770H - Koxia, Mahiru and Winter Festival
Idea by SteamTurbine
In what scenario the maximum congestion is $$$1$$$?
Assume you have a blackbox that can solve any problem instance of size $$$n-2$$$, use it to solve a problem instance of size $$$n$$$.
This is a special case for a problem called congestion minimization. While in general this problem is NP-hard, for this special structure it can be solved efficiently.
The only case where the maximum congestion is $$$1$$$, is when $$$p = q = [1,2,\dots,n]$$$. This can be proved by a pigeonhole argument — if there exists some $$$p_i \neq i$$$ or $$$q_i \neq i$$$, the total length of the $$$2n$$$ paths will be strictly greater than the number of edges which means at least one edge has to be used more than once.
Our goal now is to try constructing a routing scheme with maximum congestion $$$2$$$. We will show that this is always doable for any input. We will first show a pictorial sketch that presents the idea, and fill in the details later.
We also provide you a python script that visualize the output to help you debug, you can find it at the end of this section.
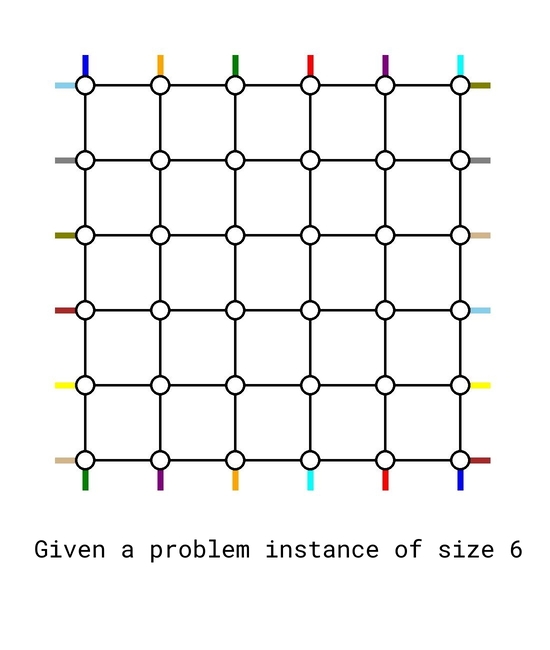
The solution is based on induction. The base cases $$$n=0$$$ and $$$n=1$$$ are trivial. Now assume we can solve any problem instance for size up to $$$k-2$$$. We will treat it as a blackbox to solve a problem instance of size $$$k$$$.
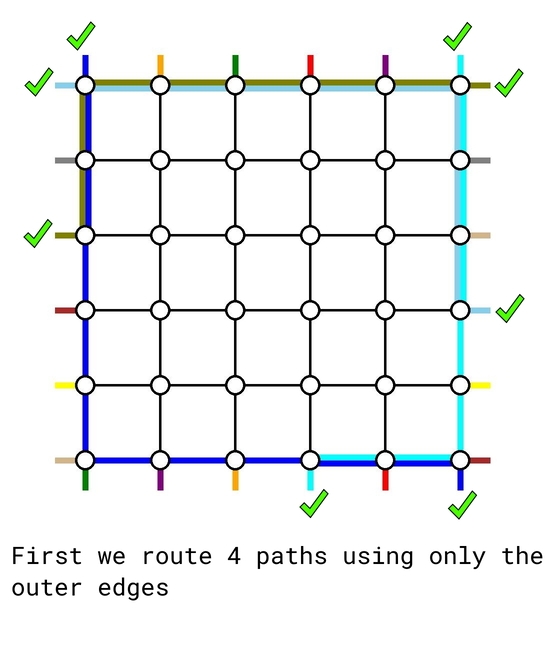
Given any problem instance of size $$$k$$$, first we route the following $$$4$$$ demand pairs using only the outer edges:
- the top-bottom pair that starts at $$$(1, 1)$$$, using the left and bottom edges;
- the top-bottom pair that starts at $$$(1, k)$$$, using the right and bottom edges;
- the left-right pair that starts at $$$(1, 1)$$$, using the top and right edges;
- the left-right pair that ends at $$$(1,k)$$$, using the left and top edges. However, if this is the same pair as above, then we route another arbitrary left-right pair using the left, top and right edges.
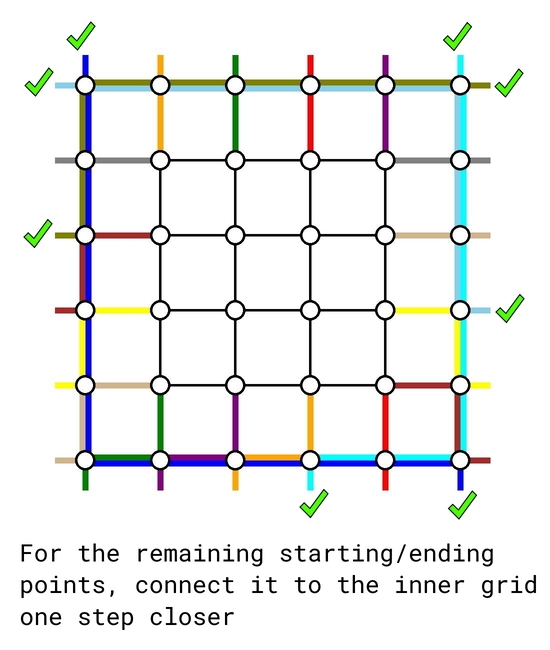
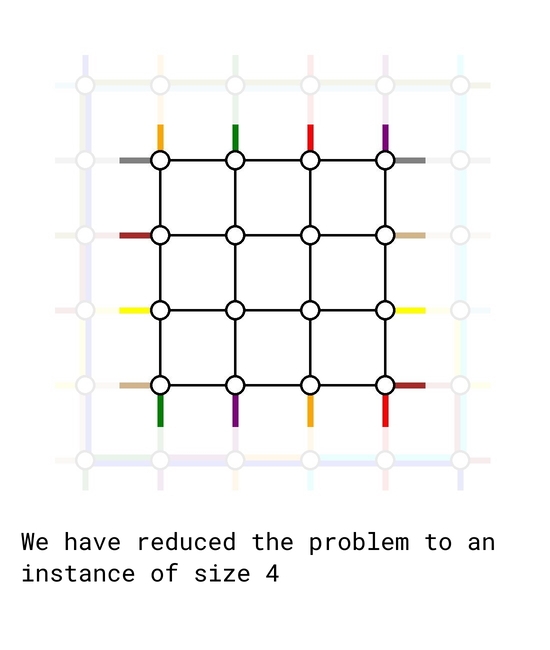
As of now, there are $$$k-2$$$ top-bottom demands and $$$k-2$$$ left-right demands remain to be routed. We simply connect their starting and ending points one step closer to the center, retaining their relative order. In such way, we reduced the problem to a problem instance of size $$$k-2$$$ which we already knew how to solve.
#include <bits/stdc++.h>
#define FOR(i,s,e) for (int i=(s); i<(e); i++)
#define FOE(i,s,e) for (int i=(s); i<=(e); i++)
#define FOD(i,s,e) for (int i=(s)-1; i>=(e); i--)
#define PB push_back
using namespace std;
struct Paths{
/* store paths in order */
vector<vector<pair<int, int>>> NS, EW;
Paths(){
NS.clear();
EW.clear();
}
};
Paths solve(vector<int> p, vector<int> q){
int n = p.size();
Paths Ret;
Ret.NS.resize(n);
Ret.EW.resize(n);
// Base case
if (n == 0) return Ret;
if (n == 1){
Ret.NS[0].PB({1, 1});
Ret.EW[0].PB({1, 1});
return Ret;
}
// Route NS flow originating from (1, 1) and (1, n) using leftmost and rightmost edges
FOE(i,1,n){
Ret.NS[0].PB({i, 1});
Ret.NS[n-1].PB({i, n});
}
// Routing to final destination using bottom edges
FOE(i,2,p[0]) Ret.NS[0].PB({n, i});
FOD(i,n,p[n-1]) Ret.NS[n-1].PB({n, i});
// Create p'[] for n-2 instance
vector<int> p_new(0);
FOE(i,1,n-2) p_new.PB(p[i] - (p[i]>p[0]) - (p[i]>p[n-1]));
// Route EW flow originating from (1, 1) using topmost and rightmost edges
FOE(i,1,n) Ret.EW[0].PB({1, i});
FOE(i,2,q[0]) Ret.EW[0].PB({i, n});
// Route EW flow originating in (m, 1) with q[m] as small as possible
int m = 1;
// special handle so congestion is 1 if possible
if (p[0] == 1 && p[n-1] == n && q[0] == 1 && q[n-1] == n){
m = n - 1;
FOE(i,1,n) Ret.EW[n-1].PB({n, i});
}
else{
FOR(i,1,n) if (q[i] < q[m]) m = i;
// Route(m+1, 1) --> (1, 1) --> (1, n) --> (q[m], n)
FOD(i,m+2,2) Ret.EW[m].PB({i, 1});
FOR(i,1,n) Ret.EW[m].PB({1, i});
FOE(i,1,q[m]) Ret.EW[m].PB({i, n});
}
// Create q'[] for n-2 instance
vector<int> q_new(0);
FOR(i,1,n) if (i != m) q_new.PB(q[i] - (q[i]>q[0]) - (q[i]>q[m]));
if (n > 1){
Paths S = solve(p_new, q_new);
int t;
// connect NS paths
FOR(i,1,n-1){
Ret.NS[i].PB({1, i+1});
for (auto [x, y]: S.NS[i-1]){
Ret.NS[i].PB({x+1, y+1});
t = y + 1;
}
Ret.NS[i].PB({n, t});
if (p[i] != t) Ret.NS[i].PB({n, p[i]});
}
// connect EW paths
int l = 0;
FOR(i,1,n) if (i != m){
Ret.EW[i].PB({i+1, 1});
if (i > m) Ret.EW[i].PB({i, 1});
for (auto [x, y]: S.EW[l]){
Ret.EW[i].PB({x+1, y+1});
t = x + 1;
}
Ret.EW[i].PB({t, n});
if (q[i] != t) Ret.EW[i].PB({q[i], n});
++l;
}
}
return Ret;
}
int main(){
int n;
vector<int> p, q;
scanf("%d", &n);
p.resize(n), q.resize(n);
FOR(i,0,n) scanf("%d", &p[i]);
FOR(i,0,n) scanf("%d", &q[i]);
Paths Solution = solve(p, q);
for (auto path: Solution.NS){
printf("%d", path.size());
for (auto [x, y]: path) printf(" %d %d", x, y);
puts("");
}
for (auto path: Solution.EW){
printf("%d", path.size());
for (auto [x, y]: path) printf(" %d %d", x, y);
puts("");
}
return 0;
}
# ---------------------------------------------------
# Visualize the ouput
# Pass the output as stdin to the script
# Only works for output with congestion at most 2
# Code by SteamTurbine Dec 2022
# ---------------------------------------------------
from PIL import Image, ImageDraw, ImageColor
from sys import stdin
import random
# Visual the ouput
# Pass the output as stdin to the script
Lines = [line for line in stdin if len(line.strip()) > 0]
n = int(len(Lines)/2)
im = Image.new('RGB', (n*150+200, n*150+200), (255, 255, 255))
draw = ImageDraw.Draw(im)
S = {(0,0,0,0)}
Dict = {}
Colors = ['orange', 'blue', 'green', 'red', 'skyblue', 'olive', 'brown', 'yellow', 'gray', 'tomato', 'tan' , 'purple', 'cyan', 'skyblue']
# use color map if n is large
if (n+n > len(Colors)):
Colors = []
for name, code in ImageColor.colormap.items():
if (name != "black" and name != "white"): Colors.append(name)
random.shuffle(Colors)
# draw blank lines
# lines to down
for i in range(1, n+1, 1):
for j in range(1, n, 1):
draw.line((i*150+20, j*150+20, i*150+20, j*150+170), fill = 'black', width = 5)
# lines to right
for i in range(1, n, 1):
for j in range(1, n+1, 1):
draw.line((i*150+20, j*150+20, i*150+170, j*150+20), fill = 'black', width = 5)
for i in range(len(Lines)):
line = Lines[i]
arr = [int(x) for x in line.split()]
pathlen = arr[0]
color = Colors[i % len(Colors)]
# draw source and sink
if (i >= n):
# x from 0 to n
y = arr[1]
x = arr[2]
draw.line((x*150-40, y*150+20, x*150+20, y*150+20), fill=color, width=12)
y = arr[len(arr)-2]
x = arr[len(arr)-1]
draw.line((x*150+20, y*150+20, x*150+80, y*150+20), fill=color, width=12)
else:
# y from 0 to n
y = arr[1]
x = arr[2]
draw.line((x*150+20, y*150-40, x*150+20, y*150+20), fill=color, width=12)
y = arr[len(arr)-2]
x = arr[len(arr)-1]
draw.line((x*150+20, y*150+20, x*150+20, y*150+80), fill=color, width=12)
for k in range(3, len(arr), 2):
(y1, x1, y2, x2) = arr[k-2:k+2]
if (x1 > x2): (x1, y1, x2, y2) = (x2, y2, x1, y1)
elif (x1 == x2) and (y1 > y2): (x1, y1, x2, y2) = (x2, y2, x1, y1)
# check if set used
if ((x1, y1, x2, y2) in S):
old_color = Dict[(x1, y1, x2, y2)]
used = 1
else:
used = 0
S.add((x1, y1, x2, y2))
Dict[(x1, y1, x2, y2)] = color
# drawline
if (x1 == x2):
if (used):
draw.line((x1*150+26, y1*150+20, x2*150+26, y2*150+20), fill=old_color, width=12)
draw.line((x1*150+14, y1*150+20, x2*150+14, y2*150+20), fill=color, width=12)
else: draw.line((x1*150+20, y1*150+20, x2*150+20, y2*150+20), fill=color, width=12)
else:
if (used):
draw.line((x1*150+20, y1*150+26, x2*150+20, y2*150+26), fill=old_color, width=12)
draw.line((x1*150+20, y1*150+14, x2*150+20, y2*150+14), fill=color, width=12)
else: draw.line((x1*150+20, y1*150+20, x2*150+20, y2*150+20), fill=color, width=12)
# draw nodes
for i in range(1, n+1, 1):
for j in range(1, n+1, 1):
draw.ellipse((i*150, j*150, i*150+40, j*150+40), fill = 'white', outline = 'black', width = 5)
im.show()
im.save("problemF.png")










I thought I did pretty bad this contest(Problem A harder than B and C) but still managed to get a positive delta.
i was not able to solve any questions , got stuck in problem A But by this contest i will get to learn a lot for sure and will improve in next contest
same happened to me
same :)
C can also be solved in O(50 * n) as for a prime to fail it should have at least 2 * p indices.(min(cnt0,cnt1,…,cntp−1)≥2). but as n <= 100 we can have p <= 50. my submission
I missed that observation, I checked all primes under 1000 because it I thought it would be reasonably high enough.
Actually, you can solve the Question with max upper bound of 25 primes since the 26th prime is 101 which can't become unavailable for x since max elements are 100
n/2 = 50 is actually O(n), so this solution (O(n^2)) is not better than tutorial
When we say an algorithm is O(n^2), it means it grows quadritically with n
Lets take n = 1000, your algorithm will need O(500*n) then, do you see why your algorithm is still quadriatic wrt n?
Bro I realized few seconds after posting, but I think we cant delete So left it like that :(
I misread B, I thought that the cost is sum(c), not max(c). Somehow I still got AC.
I loved the problems of this contest. They were enjoyable to solve. Still amazed...
Why the constraint for $$$n$$$ in problem C is too low? Since the complexity is $$$O\left( \dfrac{n^2}{\log n}\right)$$$ why not $$$n \leq 10^4$$$?
I did an $$$O\left( \dfrac{n^4}{\log n^2}\right)$$$ that wouldn't passed with higher values of $$$n$$$
It is actually O(n * sqrt(n)) :)
The author team deliberately set it as troll. We didn't mean to kill $$$O(\frac {n^4} {\log n})$$$ specially but implementations with high constant time will lead to a TLE.
and the author somehow succeeded in killing pollard rho (I don't know if that's intended, though I think it should be)
I see how you cheated C. Now stop putting shit here. Shit.
proof bro? my first AC is just skipped due to resubmission. You can easily see it barely fits in TL
Please fix the LaTeX in Solution F.
thanks for the reminder and it's ok now.
And for the solution of C, it should be if $$$x\equiv 0 \pmod 2$$$?
Thanks, you're right.
Is there any prize in this contest for individuals ranking under 2k
ah yes of course chinese remainder theorem on third task sily me for not knowing fringe ideas on suposedly easier tasks
CRT is not generally considered a fringe idea.
CRT is one of the crucial ideas you should always think about when solving a number theory related problems.
While there are many primes up to 10^18, we only need to check for the primes up to ⌊n/2⌋. This is because min(cnt0,cnt1,…,cntp−1)≥2 is impossible for greater primes according to Pigeonhole Principle. whyy??
Take prime $$$p = 53$$$ as an example, it's impossible to use only $$$100$$$ elements to fill a bucket of size $$$53$$$ and each slot has at least $$$2$$$ elements.
elaborate for this tc plz 2 10005294,10005402
Surely it's
YESwithout checking any prime. If $$$a_i$$$ are pairwise distinct, the minimum case with answerNOis $$$n = 4$$$ as mentioned above.what about this 5 10005294,10005402,10005398,10005212,10004358 ???
For $$$p=2$$$, we get $$$\mathit{cnt}_0=5$$$ and $$$\mathit{cnt}_1=0$$$.
For $$$p=3$$$, it's unnecessary to check because of Pigeonhole Principle. If we check it, we get $$$\mathit{cnt}_0=3$$$, $$$\mathit{cnt}_1=0$$$ and $$$\mathit{cnt}_2=2$$$. Ensuring $$$x \bmod 3 = 2$$$, we can calculate a proper $$$x$$$.
so answer should be YES
Surely for $$$x = 5$$$.
If min(count(i))>=2, then sum(count(i))>=p*2, which means 2*p<=n
Problem C and D are really really amazing (and easily one of the best problems I've ever come across, the proof of C, the pigeon hole principle drives me crazy!) ! I really appreciate the authors for such amazing problems. Its a pity I wasn't able to participate :(
can you please explain Pegion hole principle proof ?,why only we are checking primes less than n/2. I am still stucked in that.
CRT for 3rd task?, cannot believe..trash round
You don’t actually need to know it, I just observed that if there were two odd and even there would always be at least two even, so modulo 2 would be present. I later expanded this idea to other prime numbers.
I didn't get it, can you please elaborate on your intuition, I would like to know your thought process.
If there are two odd numbers and two even numbers, there will always be at least 2 even numbers. This is because any number you add has to be odd or even, therefore the two original even numbers will be even if an even number is added and the two odd numbers will be even if an odd number is even. This means there will be a pair divisible by 2(or gcd!=1). Now the underlying structure of this phenomenon is important. Why does this work? Well in modulo arithmetic (a+b)%m = a%m + b%m. If a is our given number, and b is what we’re adding, we can only add two distinct values (0 and 1). If the problem was simply gcd!=2, we only need to check whether there is one distinct modulo of 2. Otherwise, no matter what we add there will always be at least 2 numbers where %2==0. However, this principle itself is not only restricted to 2, it can be done for any number. For our purposes, we only need to check prime numbers although it’s not necessary to find out which prime number to check. Since n == 100, the maximum number we need to check is 50(since there needs to be at least 2 in each spot for it to fail). The main intuition came from the fact that n is reasonable small, so the solution must involve checking all the number in the array in terms of their modularity rather than gcd or other measures on the elements since the elements themselves can be quite large.
You don't need to implement the algorithm of CRT. It's just used to promise the existence of such x. In fact many contestants got AC by intuition.
Can someone explain the transitions in dp for G ?
Can anyone clear my doubt? In problem C, suppose that I have checked the remainders upto p primes , and I got such x, which satisfies the given condition( I constructed this x from first p primes where p is greater than largest element in the set). Now, how can I say that the solution I got will not contain any multiple of primes which is greater than pth prime when every element is different. I didn't get proper intuition here, so I didn't proceed afterwards :( any help will be highly appreciated.
By solution, I mean final state of array, that is (a1+x,a2+x....)
A intuitional sketch explanation is, for a large enough prime $$$p$$$, we can always find a proper value $$$\mathit{offset}$$$ so that none of $$$a_i + \mathit{offset}$$$ will be multiples of $$$p$$$.
Is this ai ai+x or is it the initial ai, (here x is same as how I constructed x using first p primes).
the initial.
But, after choosing that offset, still I may find some different x, and after addig this x to ai+ offset, I still cant say that there is no multiple of such large p.
The final $$$x$$$ is derived by merging many of $$$\mathit{offset}$$$ with Chinese Remainder Theorem, instead of summing up. So primes won't affect each other.
Now, how can you we say that this new x is not giving two multiples of primes, which are greater than the primes from which I constructed this x. It will be very helpful if this is explained in the editorial.
Maybe I didn't really get your point, so I hope it can be helpful to take this case as an example. When we list equations accordingly, just like:
. We will able to calculate a proper value like $$$x = 5$$$ using CRT. When we continue to add more equations for larger primes, the calculation is still possible as long as adding valid equations is possible.
The $$$x$$$ isn't constructed by merging the congruences of primes $$$p \le n$$$, but $$$p \le \max |a_i - a_j|$$$ over all $$$1 \le i < j \le n$$$ (i.e. the largest difference between any two values in the array). We just know that for any $$$p > n$$$ there has to exist some remainder $$$r$$$ such that $$$a_i \equiv r\ (mod\ p)$$$ doesn't appear at all. That's why we don't need to calculate them.
We don't need to check any primes $$$p > \max |a_i - a_j|$$$ since for two values $$$a_i + x,\ a_j + x$$$ to both be divisible by some prime $$$p$$$, we would also need their difference $$$|(a_i + x) - (a_j + x)| = |a_i + x - a_j - x| = |a_i - a_j|$$$ to be divisible by $$$p$$$ which is not possible if $$$p > \max |a_i - a_j|$$$.
Why x need to be constructed by only p<= maxabs(ai-aj), suppose that I have constructed such an x in this way, and I will see the array (a1+x, a2+x,.... an+x). Now, I can guarantee that no two of them hve a common factor of p for all primes <= max(ai-aj). How can I comment on p> max(abs(ai-aj)), I mean how can you say that there doesnt exists 2 multiple's of p>max(abs(ai-aj)) in the array (a1+x,a2+x...an+x). Hope you got my doubt...
I updated my original comment to show this. Message me privately if you still don't understand this.
Thank you very much for the solution.
Just a little question, why is the cost mentioned in Hint 1 of problem B 2n instead of n only?
If $$$k = 1$$$, the cost of the section which only has the value $$$n$$$ is $$$max(n) + min(n) = n + n = 2n$$$
ah yeah, my brain just stopped working and just thought that it's only the max(n) only...
I think in problem E, you need to elaborate on why the probabilities attached to the vertices are independent (in fact, they are not!), otherwise the probability of a value of $$${\mathit{siz}}_{\mathit{son}}$$$ may be non-deterministic.
Aren't they independent as the two components separated by the current edge have not been in contact with one another (which means every event within each component is independent to the other, and by extension the sizes and probablilities and whatnot)?
Precisely, what he means to say is that what you've written should have been there in the editorial.
Problem A was literally mind blowing
In C after checking for all primes <= N. After that how can we say that there will exist a number such that gcd will be 1 for every pair.
If no prime was found where every possible remainder appeared at least twice, there has to be at least one remainder for every prime such that $$$x \equiv r\ (mod\ p)$$$ works. We know that such $$$x$$$ that fits all of the congruences always exists because the Chinese remainder theorem says so. (Go to the proof-section for the proof of the theorem).
Did anyone else miss A because they sorted array b?
I solved A after B,C,D with four WA's because of this.
Why is my Python PriorityQueue solution too slow in PyPy. 187389454
In Python 3.8 it is faster: 187389600
Can someone explain why "Then there is a way to make $$$p$$$ a permutation iff there is a way to assign a direction for every edge such that every vertex has one edge leading into it. " is true in problem D's editorial?
For choosing one element from $$$a_i$$$ and $$$b_i$$$, we can consider "choose $$$a_i$$$" as "edge $$$(a_i, b_i)$$$ is directed as $$$b_i \rightarrow a_i$$$".
In Solution Para-5 Line 3 , Why it min(cnt,....)>=2 ? Can someone please elaborate this line.
refer to the last paragraph
;_;
Thank you very much for the round, I enjoyed it very much and will also remember it for very long as the round I reached gm! I liked the problems very much, especially problem D. The underlying idea was very cute and unexpected, I wish to see such problems more often
Why are you leaving CP?
Graduated from university and no longer have the opportunity to participate in the ICPC, so I will not keep training for a long time anymore.
Hi, I have two questions related to editorial for Problem C.
"Yes" condition:
Question 1: so, do I correctly understand, that, instead of checking Yes, we are checking No?
So, "No" condition is next:
There is a prime number $$$p$$$ for which there are two elements $$$a_i$$$ and $$$a_j$$$ such $$$(a_i+x)\equiv 0\text{ } (\text{mod }p)$$$ and $$$(a_j+x) \equiv 0\text{ }(\text{mod }p)$$$ for any positive integer $$$x$$$.
By subtraction two equations we have: $$$a_i \equiv a_j \text{ }(\text{mod }p)$$$.
Question 2: do we need just to check for given $$$p$$$ if two elements have same remainder modulo $$$p$$$? I mean, that if we can find such $$$p$$$ and such two elements then answer is No?
If so, then it contradicts with next statement in editorial:
Because it should be $$$\text{max}(\text{cnt}_0,\text{cnt}_1,…,\text{cnt}_{p−1}) \ge 2$$$ instead of $$$\text{min}(\text{cnt}_0,\text{cnt}_1,…,\text{cnt}_{p−1}) \ge 2$$$.
Or I am unable to understand the logic why $$$\text{min}$$$ is used instead of $$$\text{max}$$$.
$$$a_i \equiv a_j \pmod p$$$ means a slot in bucket $$$cnt$$$ is banned, but maybe other slots are still available.
For a bucket like $$$\mathit{cnt} = [111, 222, 1, 333, 444]$$$, although $$$\max = 444$$$, we have $$$\min = \mathit{cnt}_2 = 1$$$, so we can keep $$$x \equiv 3 \pmod 5$$$ to get a proper $$$x$$$ such that "$$$5$$$ should divide at most one $$$b_i$$$" holds.
I'm sorry, but I don't understand...
Consider smaller example instead of $$$cnt=[111,222,1,333,444]$$$, just $$$cnt=[2,2,1,2,2]$$$.
Array $$$a=[5,10,6,11,7,8,13,9,14]$$$ gives such $$$cnt$$$ modulo $$$5$$$. You are saying that you can choose $$$x \equiv 3\text{ }\left(\text{mod }5\right)$$$. OK, but with $$$x = 3$$$ we have $$$b=[8,13,9,14,10,11,16,12,17]$$$. But $$$gcd(14,10)=2$$$, so, $$$x = 3$$$ is a wrong number.
This
NOis caused by prime $$$2$$$ instead of prime $$$5$$$. Only if condition $$$\min(\mathit{cnt}) \leq 2$$$ holds for each prime, we outputYES. For example, $$$a = [6, 12, 18, 24, 30, 36, 48, 54, 60]$$$ and $$$x = 13$$$ (if we set $$$x \equiv 1 \pmod 2$$$, $$$x \equiv 1 \pmod 3$$$ and $$$x \equiv 3 \pmod 5$$$).If we are able to find a prime number such that count of any of its remainder is 1 than ans should be yes and why do we need to check for other primes?
we are considering the cases after adding the value x. so in that sense why we need to take the modulo we assumed that we have added x but the modulo we have taken is not representing it
I am really confused on how the solution worked
If possible please breakdown a test case into small pieces, I tried it but got messed up
Also please link similar problems(if any)
From "We are able to find a prime number such that count of any of its remainder is 1", we can only derive that it's possible to choose a proper $$$x$$$ such that $$$p$$$ won't divide two or more of $$$b_i$$$. But we don't know if it holds for other primes.
Consider the test-case, n=4 a={8,9,11,13}
if p=2 we have cnt={1,3} if p=3 we have cnt={1,1,2}
so usnig CRT we will find the solution for x=0 (%2) x=0 (%3) || x=1 (%3) so we can get a solution as x=6 here since we can not have solution with x=1(%3) so how can we say for other cases if we only had equations(given below)a solution will exist x=0 (%2) x=1 (%3) since in above test case if we only considered these 2 equations there will not be a possible solution
CRT always can give you solutions as long as you input correct congruence equations. A solution for "x=0 (%2) x=1 (%3)" is $$$x = 4$$$.
How does a single slot verify we can have different values for all numbers giving different remainders.
CRT. Different prime numbers won't affect each other.
When $$$a_1 \bmod p = a_2 \bmod p = c$$$, $$$x$$$ should not be $$$(p - c) \bmod p$$$. (Because if $$$x\equiv (p-c){\pmod {p}}$$$, just like $$$x=p-c$$$, then $$$(a_1 + x) \bmod p = (a_2+x)\bmod p = 0$$$, which means $$$a_1+x$$$ and $$$a_2+x$$$ at least have one same factor $$$p$$$ and $$$\gcd(a_1+x,a_2+x)\not = 1$$$.)
The constraints are $$$x\not = c$$$, where $$$c$$$ is that at least there is a pair of $$$a_i$$$ and $$$a_j$$$ that meets $$$a_i \bmod p = a_j \bmod p=c$$$. So if there is one of the counts of $$$a_i \bmod p$$$ that is less than $$$2$$$, we can get equation $$$x \equiv (a_i \bmod p) \pmod p$$$. For all $$$p$$$, we can get a group of equations. Because there is no limitation on $$$x$$$, anyway we can solve one $$$x$$$ by CRT or other ways.
Good contest but why were the samples so weak ?
Too strong samples will imply correct solutions. I hope we have set it basically properly.
Instead of dealing with the condition of or-sum being $$$y$$$ directly, we aim to find solutions to $$$A_1|A_2|A_3|\ldots|A_n \subseteq y'$$$, for all $$$y' \subseteq y$$$. And use PIE to get the actual answer.
Focus on a single value of $$$y'$$$. $$$A_1|A_2|A_3|\ldots|A_n \subseteq y'$$$ can be represented as $$$A_i \subseteq y'$$$. Let $$$C$$$ be the array of toggled bits in $$$y'$$$ copied $$$n$$$ times. Then we can represent this as finding the parity of the number of solutions to $$$\sum B_i \cdot 2^{C_i}=x$$$, where $$$B_i$$$ can be chosen to be either $$$0$$$ or $$$1$$$. This is for because each bit inside $$$y'$$$, we have a choice to turn it on or off for elements of $$$A$$$. And we want to count the number of such ways to do that, which leads to us solving the above problem. This is a giant subset sum problem that is not feasible to solve, so let us instead try to make some observations about it.
Suppose that $$$C_a=C_b$$$, then we will perform the operation $$$\text{swap}(B_a,B_b)$$$. This operation is an involution over all solutions to $$$B$$$. The parity of the number of solutions is equivalent to the parity of the number of fixed points of the involution.
Consider the solutions of $$$B$$$ as vertices of a graph. We will add a directed edge from solution $$$B_1$$$ to $$$B_2$$$ if $$$B_2$$$ is obtained by swapping $$$B_{1,a}$$$ and $$$B_{1,b}$$$. Now, each vertex has exactly $$$1$$$ outgoing edge.
Notice that if we traverse the edges twice, we will end up back at the same vertex since swapping $$$B_a$$$ and $$$B_b$$$ twice does nothing. Therefore, each connected component of the graph either looks like $$$a$$$ with a self-loop to itself or $$$a \leftrightarrow b$$$.
If we delete all connected components of the form $$$a \leftrightarrow b$$$, the parity of the number of vertices does not change since we deleted an even number of vertices. The number of vertices that are self-loop components are those where swapping $$$B_a$$$ and $$$B_b$$$ changes nothing. That is, those solutions where $$$B_a=B_b$$$.
We want to find the value of $$$[x^k] \prod (1+x^{2^{C_i}})$$$ under mod $$$2$$$. Realize that $$$(1+x^{2^k})=(1+x)^{2^k}$$$. Therefore, $$$\prod (1+x^{2^{C_i}}) = \prod\limits (1+x)^{2^{C_i}} = (1+x)^{\sum 2^{C_i}}$$$. Finding $$$[x^k] \ (1+x)^z$$$ under mod $$$2$$$ is easy.
Therefore, we should only consider solutions where $$$B_a=B_b$$$. However, since $$$C_a=C_b$$$, it is equivalent to deleting $$$C_a$$$ and $$$C_b$$$ and adding $$$C_a+1$$$ instead. If we continue this process until there are no duplicate elements in $$$C$$$, $$$C$$$ would end up being the toggled bits of $$$ny'$$$.
Note that it is sufficient to calculate the total xor of $$$A_i$$$ over all valid arrays for any $$$i$$$ since this value is same for all $$$i$$$.
So the total xor of element $$$A_i$$$ is $$$\bigoplus\limits_{y' \subseteq y} \bigoplus\limits_{\substack{v \in y' \\ (x-v) \subseteq (n-1)y'}} v$$$.
Actually, we can focus on parity that some bit is contained in $$$A_i$$$. So solutions to $$$\bigoplus\limits_{y' \subseteq y} \bigoplus\limits_{\substack{bit \in y' \\ (x-bit) \subseteq ny'-bit}} bit$$$. This achieves $$$O(y \log y)$$$ complexity.
Do remember to output $$$0$$$ if $$$n$$$ is even as we only calculated the contribution of a single element of $$$A$$$.
This is how I solved F —
Firstly, $$$C(N,R)$$$ odd, if and only if $$$R$$$ is a subset of $$$N$$$. This comes from lucas theorem.
This is the only pre-requisite one need for solving this problem.
Let's assume that $$$N$$$ is odd; otherwise answer is just zero.
Let the on bits in $$$Y$$$ be $$$b_1,b_2,...b_k$$$ (powers of 2).
Now we can write $$$a_1+..+a_n = x$$$ as $$$c_1*b_1+c_2*b_2+...+c_k*b_k=X$$$, where $$$1 \le c_j \le n$$$.
Once we have fixed a particular set of $$$c_1,c_2,...c_k$$$, no of ways to chose such $$$a_i$$$ is $$$T=C(n,c_1) * C(n,c_2) * .... * C(n,c_k)$$$
If T is odd, it adds all bits $$$b_j$$$ where $$$c_j$$$ is odd.
One necessary condition for $$$T$$$ to be odd is each $$$C(n,c_i)$$$ is odd, implying $$$c_i$$$ is a subset of $$$n$$$.
Let $$$d_1, d_2, ..., d_l$$$ (powers of 2) be the bits of $$$n$$$. We can also split each $$$c_i$$$ in these bits. Namely,
$$$c_i = e_{i,1} d_1 + e_{i,2} d_2 + ..... + e_{i,l} d_l$$$.
Now, $$$X$$$ can be written as $$$X= \sum e_{i,j} b_i d_j$$$.
Let's call this multiset of powers of 2, whose subset we should pick to form $$$X$$$, $$$S$$$. Namely,
$$$S = (b_i* d_j )$$$ for all $$$1 \le i \le k$$$ and $$$1 \le j \le l$$$
I will leave this $$$S$$$ and come back to it later.
The necessary and sufficient conditions for OR $$$Y$$$ is
- At least one among each $$$e_{i,1}, e_{i,2}, ..., e_{i,l}$$$ is one, because we want $$$c_i \ge 1$$$
Since $$$N$$$ is the odd, one among $$$d_1, d_2, ..., d_l$$$ is $$$1$$$, lets assume $$$d_1 = 1$$$.
Note that total xor has a contribution from $$$b_i$$$ only if $$$e_{i,1}$$$ is 1.
$$$Y_1,Y_2,...Y_m$$$ be the subsets of $$$Y$$$. Instead of finding total XOR when OR is $$$Y$$$. Let's find total XOR when OR is a subset of $$$Y_o$$$ for each $$$1 \le o \le m$$$.
EOD, we can use PIE on these to find the total XOR when OR is exactly $$$Y$$$.
Let's count the contribution of each $$$b_i$$$ when OR is subset of $$$y_j$$$.
$$$e_{i,1}$$$ must be 1, $$$b_i$$$ should be present in subset of $$$y_j$$$.
We can change this problem to an earlier defined problem, where we will have to find sum $$$X$$$,
using a subset bit of $$$b$$$ which forms $$$y_j$$$ and $$$d$$$ namely multiset $$$S'$$$, with the only condition that $$$e_{i,1}$$$ must be $$$1$$$.
To simplify things, we can remove $$$b_i*d_1$$$ from $$$S'$$$ (let's call this multiset $$$T$$$) and find the sum $$$X' = X-b_i$$$.
Now, our original problem has been reduced to counting the no of subsets in multiset $$$T$$$, which sum $$$X'$$$, the only thing we are interested in is if it's odd or not.
Let $$$T = T_1, T_2, T_3,... $$$ be the multiset, if it contains two values $$$T_i = T_j$$$,
then no of ways with sum $$$X'$$$ when coefficient of $$$T_i$$$ as $$$1$$$ and $$$T_j$$$ as $$$0$$$ is equal to no of ways with sum $$$X'$$$ when coefficient of $$$T_i$$$ as $$$0$$$ and $$$T_j$$$ as $$$1$$$.
These ways cancel each other out, and we are left with finding no of ways when both coefficients are either $$$0$$$ or $$$1$$$.
For these, we can remove $$$T_i=T_j$$$ from multiset $$$T$$$ and replace it with $$$2*T_i$$$.
We can keep repeating this exercise until all the elements in $$$T$$$ are unique.
When this happens, $$$T$$$ will be nothing but a binary representation of the sum of all values in $$$T$$$.
Then to check if $$$X'$$$ can be formed using values present in $$$T$$$ is just checking if $$$X'$$$ is a subset of $$$T$$$.
Overall we will have to find the contribution for each bit in each subset of $$$Y$$$, and that can be computed in $$$O(1)$$$.
Overall time complexity $$$O(Y*logY)$$$.
Chinese Reminder Theorem. -> Chinese Remainder Theorem
Thanks for correcting and it's fixed now.
In $$$C$$$, I understand why for each prime $$$p$$$ there must be least one $$$0 \le v < p$$$ where $$$a_i \equiv v$$$ mod $$$p$$$ occurs at most once. I also understand that if the previous condition is satisfied, for any set of primes, for each $$$p$$$ of them we can choose $$$0 \le v < p$$$ where $$$a_i \equiv v$$$ mod $$$p$$$ occurs at most once and construct $$$x$$$ that satisfies the congruences $$$x\equiv -v$$$ mod $$$p$$$ using Chinese remainder theorem, i.e., to make every $$$p$$$ divides at most one $$$a_i+x$$$ .
But what guarantees that after choosing a set of primes we will not end up with a new prime $$$p_{new}$$$ by which some $$$a_i+x$$$ and $$$a_j+x$$$ will be divisible? and if we include $$$p_{new}$$$, what guarantees that another newer prime will not appear and continue like this indefinitely? We already know a trivial case that causes this, i.e., when we have $$$a_i = a_j$$$. But what guarantees there are no other cases that can cause this?
Instead of chosing $$$a_i \equiv v$$$ mod $$$p$$$. You should choose $$$v \equiv -a_i$$$ mod $$$p$$$. This will ensure that for each prime p, there exists atmax one such $$$a_i + x \equiv 0$$$ mod $$$p$$$ for each prime $$$p$$$.
Yes I understand how we should choose the moduli for a set of primes to ensure every prime of them divides at most one $$$a_i+x$$$, but this is not my question.
My question is why is it guaranteed that after doing this for any set of primes there will not always appear another prime that was not in the set and will divide some $$$a_i+x$$$ and $$$a_j+x$$$.
A trivial example for this is an array of $$$2$$$ values with $$$a_1=a_2=v$$$. For any set $$$S$$$ of primes we can create an $$$x$$$ such that no prime of them divides $$$v$$$, but we will always end up with a prime that was not in $$$S$$$ and divides $$$v$$$ ($$$a_1$$$ and $$$a_2$$$). So the question is, apart from an arbitrary array with some $$$a_i=a_j$$$, what guarantees that there are no other cases that can cause this?
It looks like the answer of my question is here.
Any prime that divides any $$$2$$$ values divides their difference as well. The difference between any $$$a_i$$$ and $$$a_j$$$ will still be the same after adding $$$x$$$ to both. This means we have an upper bound for the primes that can divide any $$$a_i+x$$$ and $$$a_j+x$$$ as long as $$$a_i$$$ and $$$a_j$$$ are different. When $$$a_i=a_j$$$, no upper bound exists as any prime divides $$$0$$$.
Why BenQ uses Rust for solving H in Goodbye 2022 contest? Is there any benefits over C++?
so where can I find the Chinese tutorial
It's available now, sorry for being late.
In Problem C you didn't use the condition "all $$$a_i$$$ are different". So why do I have to check the trivial NO? What makes the solution incorrect when some $$$a_i$$$ are the same?
This is what confuses me when I come up with this solution.
https://mirror.codeforces.com/blog/entry/110754?#comment-986999
above argument fails when ai=aj
I have another idea for H. First we solve by hand for $$$p_i=q_i=n-i+1$$$, it is easy using idea for $$$n=2$$$. Now whenever $$$p_i>p_{i+1}$$$, the corresponding paths must intersect and so you can untangle them and swap $$$p_i$$$ and $$$p_{i+1}$$$. So we can just do bubble sort and do $$$O(n^2)$$$ such subroutines to modify into correct $$$p$$$. Same idea for fixing $$$q$$$.
Thanks for the contest, very interesting problems.
Can you elaborate your idea in more detail?
how to prove that [n,1,n-1,2,n-2,3,n-3,4,....] is the optimal solution for B ??
got it , thank you :)
Problem G has such a simple statement. It seems so unexpectedly hard to me.
Seems a really nice problem, gonna try it when I reach red.
Why is the greedy strategy for question A correct? Is there any proof of the correctness of the first solution or the second?
I added a short explanation about the sorting approach — hope that helps!
Really a nice contest for last of 2022.
For E, is the expression for updating the probabilities very intuitive? I mean, mathematically, I got the expression but not sure if there is some obvious way to state that both probabilities will become (Pu + Pv)/2
Actually, we can consider the move operation as "swap or don't swap with both $$$\frac 1 2$$$ probability", no matter whether $$$u$$$ and $$$v$$$ are occupied or not. Therefore, $$$p_{\mathit{new}} = \frac {p_u+p_v} {2}$$$.
How do you prove that probability of swapping is equal to $$$1 \over 2$$$?
just simple case-analysis for all $$$4$$$ cases. (node $$$u$$$ / $$$v$$$ occupied or not)
In E, why isn't (or I just didn't see in code) $$$sum_u$$$ updated while calculating the contribution each edge gives to the final answer, when $$$p_u$$$ was changing?
Because it's not changing.
Each edge split the tree into two components, and you can see that a butterfly cannot fly from one component to the other before the operation on this edge.
Got it. Very thanks :)
Please ensure that you have gotten why we claim $$$|\mathit{siz}_{\mathit{son}} - \mathit{siz}^0_{\mathit{son}}| \leq 1$$$ before think about later parts.
Thanks >_- I was thinking too complicatedly.
I think the butterflies don't cross that edge.
That's the very point.
In Problem-C,
In the min case, cnt[i]=2 for every 0 <= i < p where p is a prime number. So, 2*P=n tends to P = floor of n/2. That is also proved by Pigeonhole principle.
in problem C can you find such x for yes
It is theoretically possible by using CRT as the editorial mentioned, but the result may be very large.
Could you please explain how theoretically it is possible to use CRT?
For some Prime P1, we need x1 to be added in the array to make at most 1 element divisible by P1, but how to find x so that at most 1 element is divisible by all primes smaller than n/2?
solve congruence equations like:
Got it. Thank you!
In question C If min(cnt)<2 holds for all primes, then we can list certain congruence equations and use Chinese Reminder Theorem to calculate a proper x I don't want to go to too many details on how to find x but can someone explain why the Chinese Remainder Theorm can be used here?
CRT is used to solve congruence equations, for example, CRT tell us "$$$x = 13$$$ is a solution" if we set $$$x \equiv 1 \pmod 2$$$, $$$x \equiv 1 \pmod 3$$$ and $$$x \equiv 3 \pmod 5$$$.
In problem D I have considered bipartite graph from number to position, the solution is very similar actually. To verify feasibility of assignment, we check that each connected component contains the same amount of numbers and places.
For D, what was the intuition to set up the graph like so? I've gotten the 2 lemmas but I couldn't figure out how to set up the graph like that. If anyone can provide some insight, that would be great.
Refer to https://mirror.codeforces.com/blog/entry/110754?#comment-987007. Honestly it needs some inspiration or experience.
Thanks! I understood that after looking at the editorial, just couldn't figure out how to model it as a graph before reading the editorial. Might just need to practice more I think.
can anybody please explain what hints towards using graph in problem D? Is there so observable pattern?
Can someone please explain how D problem is converted to a graph problem? Like what exactly are the edges and the vertices in the said graph? Thanks in advance :)
Following is my approach, please correct me if I am wrong (I think it would TLE anyway tbh)
I could figure out lemma 1 and lemma 2 by myself and thought that I can make a directed graph by taking the elements in array a and b as vertices and every a[i] and b[i] connected to a[i+1] and b[i+1] except the last node. Then I traverse through this graph twice and check if I can create a path with unique vertices and reach the terminal node (i.e. check if P is a permutation) one path starting from a1 and the other from b1. Every node is marked 1 if a path through the node exists or 0 other wise. Now we can check for every (a[i], b[i]):
if a[i] and b[i] are both marked 1 and if they are equal that means a path through both the vertices exists and any of them can be chosen during that round (i.e. c[i] can be anything so multiplying answer with n)
if they both are marked 1 but are not equal then c[i] can only take 2 values in that round (so multiplying answer with 2)
if only one of them is marked 1 then c[i] can only take that one value so multiplying answer with 1
else no path exists so the answer is multiplied with 0
Refer to https://mirror.codeforces.com/blog/entry/110754?#comment-987007. They're not really for some clear meanings, but we can claim 2 problems are equivalent and this is enough.
2 2 109 111 119 110
for this solution Answer is 229 by editorial solution But the answer is 230
You have to apply all $$$m$$$ operations sequentially.
Can anyone explain the logic behind only taking prime numbers upon n/2 in problem C?
pegion hole ! for primes over n / 2 there exists an r < p where cnt[r] < 2 (cnt[x] = number of array elements that have reminder x when devided by p)
In E, what is inv2? And why do we multiply delta by it?
UPD: Ok, inv2 means division by 2, but why do we divide delta by 2?
If we use
delta, it means we apply the move operation always, no matter the direction of edges. But actually, it's randomly chosen from two directions.In D, what does "if (edge != 2 * vertex) ans = 0;" this implies?
Refer to the editorial (Paragraph "We can transform this into a graph problem..."). We need to check whether $$$|V| = |E|$$$ or not.
in problem c
given the input a = [5, 7], then [5 mod 2, 7 mod 2] = [1, 1]. 1 appears twice so the minimum multiplicity is equal to 2. Above in paragraph 3 you say print NO. if x=2,then the gcd(5+2, 7+2) = gcd(7, 9) = 1. Isn't it wrong to print no while there is an x for which
gcd(a_{1}+x, a_{2}+x) = 1.I'm probably wrong I just want someone to explain how.
1 appears twice but 0 doesn't appear, so the minimum multiplicity is $$$0$$$ instead of $$$2$$$.
can anyone please post link of the classical problem mentioned in hint 1 of problem E
Can someone provide a easir explanation for problem C
in problem D why edge!=2*vertex
Scroll up the mouse wheel a few times to see.
Can somebody explain how the sigma pi formula came in F’s editorial and how did this helped in solving the problem. As we are not interested in number of sequences but xor of such ones. Moreover $$$\binom{ny}{x}$$$ is the solution of equation $$$t_1 + t_2 + … + t_n = x$$$ where each $$$t_i$$$ can take any value between 0 and y by Vandermode identity, then how are we ensuring that each $$$t_i$$$ is also subset of y?
We can't ensure that each $$$t_i$$$ is a subset of $$$y$$$ so we need inclusion-exclusion principle (Hint 4).
Can someone explains why in problem C, we only consider prime number ?
nvm i got it
In problem C, we only need to iterate through all prime numbers, then why are we checking for each number from 2 to n/2 ??
checking prime numbers in $$$[2, \lfloor \frac{n}{2} \rfloor]$$$ is enough, I just got lazy to sieve prime numbers when implementing it.
Hi!
I am wondering, for problem C, is it equivalent to check all integers up to $$$\lfloor n/2 \rfloor$$$ instead of primes? The criterion for NO is exactly the same. And for the existence of $$$x$$$, we could also create the equations in the same way, (in which the modulo may not be pairwisely coprime, but we can always convert it to one that is), and use CRT to solve it.
Actually, I think checking integers is more essential, right?
checking prime numbers in $$$[2, \lfloor \frac{n}{2} \rfloor]$$$ is enough, I just got lazy to sieve prime numbers when implementing it.
So instead of using primes upto u/2 -> how traversing all numbers upto n/2 won't change our answer ?
I mean can you prove ?
like if you run out slots when checking $$$6$$$, then you must run out slot when checking $$$2$$$ or $$$3$$$, so it's redundant to check composite numbers.
ok ok i got that like if 2 and 3 are dividing at most one numbers then obviously 6 will divide at most one number.
Can anyone explain the problem D why we need to build the graph like this and why we can find the answer by assigning directions for each edge? I can't imagine how it works
gr8
How to get the x if it exist for Problem B by using CRT? what's the mod function?
mod is
%in C++; CRT is https://oi-wiki.org/math/number-theory/crt/In the problem C , why we are checking prime numbers only
https://mirror.codeforces.com/blog/entry/110754?#comment-997851
Got it , thanks
Just read the editorial for Problem D. I think you missed a third category for the additional edge. Consider a case where a connected component of the final undirected graph is the following: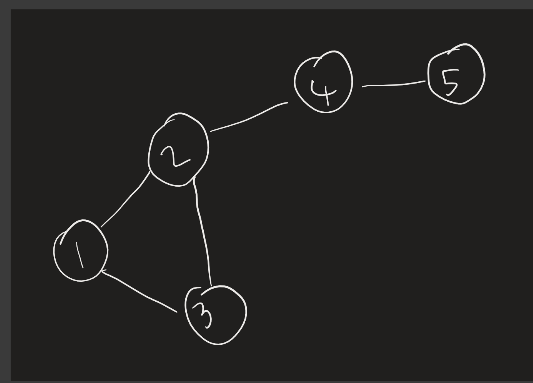
The edge 2-4 is neither a cycle edge nor a self loop edge. While the final answer will remain the same, I think clarifying this would be helpful for anybody who looks at the tutorial in the future.
Please feel free to correct me if I'm wrong.
Hello! Actually, what the editorial said is, components can be categorized into two types — "cycle component" or "self-loop component", by the size of their cycles. The component in your graph is also counting as a "cycle component" although it's not only a cycle.