In this problem it was needed to check the constraints described in statement. You can use two sets here. You should insert diagonal elements of matrix into the first set, and the other elements into the second. Element ai, j belongs to the main diagonal if i = j and belongs to the secondary diagonal if i = n - j + 1. After you split all elements into sets you should check if the sets sizes are equal to one and the elements from this sets differ from each other.
Let's notice that after Valera run 4·a meters he will be in the same point from which he started. Valera will have run i·d meters before he gets i-th bottle of drink. Let's calculate the value 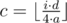 — how many laps he will run. Then he have already run L = i·d - c·4·a meters on his last lap. It is easy to get Valera's position from this L. For example, if 2·a ≤ L ≤ 3·a then Valera will be in the point with coordinates (3·a - L, a). You can consider the other three cases in the same manner.
— how many laps he will run. Then he have already run L = i·d - c·4·a meters on his last lap. It is easy to get Valera's position from this L. For example, if 2·a ≤ L ≤ 3·a then Valera will be in the point with coordinates (3·a - L, a). You can consider the other three cases in the same manner.
First of all let us notice that it must be only one 0 in d. Also d[start] = 0 means that start is the vertex from which Valera calculated the distance to the other vertices. Let's notice that every vertex u with d[u] = i must be adjacent only to the vertices v such that d[v] ≥ i - 1. Besides there is always must be such neighboor v0 of u, that d[v0] = i - 1. Let's build sought graph by adding one vertex to the existing graph. We will add vertex in order of increasing their distance to start. Initially, we have one vertex with number start in our graph. When we add vertex u with d[u] = i let's consider such vertices v that d[v] = i - 1. Let's choose the vertex with minimal degree among them. If this value is equal to k, then there is no solution. In other case let's add u to our graph and add the edge (u, v) to the answer. If there are no vertices with distance i - 1 to start then the answer is also - 1. If everything fine we will get the answer which is tree, so the number of edges in it equals n - 1 ≤ 106.
This problem can be solved by using dynamic programming. Let's calculate d[i][type] — the number of correct ways to fill the prefix of length i so that the last filled cell has one of the 5 types. These types are the following:
the cell contains "0"
the cell contains "1" and the cell to the left of it contains bomb
the cell contains "1" and the cell to the left of it doesn't contain bomb
the cell contains "2"
the cell contains bomb
When we try to fill next cell we check two conditions. Firstly value of the filled cell in given string must be equal to either what we want to write or "?". Secondly new prefix must remain filled correct. For example, if we are in state (i, 1) (it means that the cell i contains "0") then we can fill next cell by "0" and go to the state (i + 1, 1) or fill next cell by "1" and go to the state (i + 1, 3). We cannot write "2" because both neighbours of the cell with "2" must contain bomb. Obvious, we cannot place bomb after "0". Note that, when we place "1" after "0" we go to the state (i + 1, 3), but when we place "1" after bomb we go to the state (i + 1, 2). You can consider other ways of going from one state to another in the same manner.
Let's consider the case when the last move of the robot is equal to "R". If the last move is equal to "L" then we can replace all "L" by "R" and vise versa and the answer doesn't change. Let's show that Valera doesn't need more than one obstacle. Suppose Valera placed obstacles somewhere. We will say that the number of obstacle is the number of cell containing it. Let's consider the rightmost obstacle obs1 among the obstacles with negative numbers and the leftmost obstacle obs2 among the obstacles with positive numbers. Obvious robot cannot go to the left of obs1 and to the right of obs2. So the needed number of obstacles is not greater than two. Let's show that Valera doesn't need to place obstacles to the cells with numbers greater than zero. Suppose he place obstacle to the cell with number a > 0. If robot doesn't try to go to this cell then its obstacle is out of place. If robot try to go to this cell then it will visit finish cell more than once. It is because robot needs to go to the right on its last move, but it can't do it from cell a - 1 and it has already visited all cells to the left of a. So Valera doesn't need more than one obstacle and its obstacle must have number less than zero.
Let's now check if Valera can do without obstacles. If so the robot won't skip moves and will stop in some cell. Than Valera can choose this cell as finish and the answer will be one. We have to consider only one case when Valera must place one obstacle.
Firstly let's notice that if Valera place obstacle to some cell, the finish cell can be restored uniquely. It means that the number of ways to choose where to place obstacles and finish cell is equal to the number of ways to choose one cell to place one obstacle. Suppose Valera placed obstacle in the cell with number b < 0 and robot completed its instructions successfully. Notice, that in that case robot skipped some moves of type "L", completed all moves of type "R" and went to the right on its last move to the unvisited cell. If we shift Valera's obstacle to the right on one cell then robot is going to skip not less moves of type "L" than in the previous case. It means that the finish cell can either go to the right or remains the same. But last time robot visited this cell on its last move, so it is going to visit a new finish cell on its last move either. This means that there is such cell p < 0 that if Valera place obstacle to the cells c ≥ p then robot will be able to complete its instructions successfully, but if Valera place obstacle to the cells d < p then robot will not. This cell p can be found by using binary search and simple simulation on each iteration. Time complexity is O(n log n).











probably for the first time in my life, i have used the function
fmodof C++ (to solve problem B).i always used to think this was a useless function! :D
fmod is a great function... but less of people know about it...
Oh, I was seeking for such a function... Thanks anyway.
It's so great.Thank you for sharing this function.
Hi,
I've got a question about Problem E. I think the solution doesn't always exist, but the problem description doesn't mention this and neither does the editorial.
Let RLR be an example. If we don't place any obstacles, we end at position 1, which has been visited before. We can't place an obstacle on position 0, so the only other option is to place the obstacle at position 1. In that case, we end at position 0, which is also an invalid result. What's the correct answer for these cases?
A similar case is found in test#4 in system test ... The output should be zero at that case.
For the problem E I have an O(n) algorithm: http://mirror.codeforces.com/contest/404/submission/6085167. I only set 0 or 1 obstacle on the line. If I don't set any obstacle, and the robot makes a valid way, just print 1. Else, all I need are the minimum position of the robot for all process and the last position if I set an obstacle on position "pos" (pos>0).
nice algorithm~~~
I don't have time to solve problem D
In problem C, Why last test case i.e.
5 4
0 1 1 1 4
returns '-1' ?
can this be the answer :
4
1 2
1 3
1 4
2 5
your answer is valid if input 5 4 0 1 1 1 2
well, there is no vertex can be in distance 4 if there is no vertex in distance 2 and 3. so there are no answer
That means all the edges are of 1 unit length. Am i right? if yes, then it is not mentioned in question.
exactly. its been clarified during the contest
Problem C. Restore Graph ***** The distance between two vertices is the minimal number of edges in the path between themc
Thanks. Just checked.
Can anyone explain me Minesweeper 1D in detail. I'm unable to find out the recurrence ? If you have code for this question then please add comments in Code so that I'm able understand the logic as well as Code . Thank You !!!
For Problem C — Restore Graphs. What is test case number 35 ?
My submission was also getting Wrong answer on that test case... The problem with my code was "int overflow" when I was multiplying v[i-1].size() * (k-1) for checking for the -1 case.
If you have a doubt regarding the test case of Problem C, then check this link.