The problem statement can be referred from here. In short you are given an array "prices" and you need to determine the maximum profit one can earn by doing atmost k trades. You cannot buy a stock unless you have sold the previous one. The dynamic programming solution to this is well known and solves the problem in O(nk) time but did you know a stack+heap solution to this also exists that solves the problem in O(n+nlogk) time? This second solution is not as famous and I have only ever managed to find 2 or 3 articles explaining the solution and that too were not very clear and full of symbols instead of a visual explanation. So here in this article I will try to explain this solution as clearly as I can.

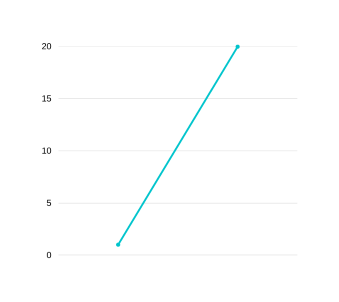
Okay so first things first, lets look at what are the inputs that we have at hand — An array named "prices" containing the price of stocks on each day and an integer "k" telling us how many trades we can carry out at max. An important thing to note here is that the prices array can be converted to a line graph for visualization. For example the array [1,5,3,8] can be represented as :

GRAPH 1

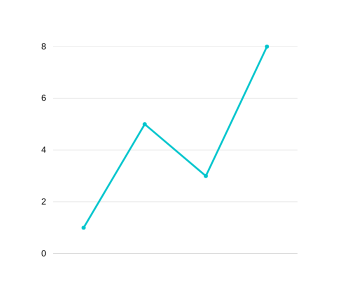
Another thing we need to define are "peak" and "valley". Peaks are nothing but tip of the mountains in the line graph and valleys are the dips or the upside-down mountains. In our graph above peaks are at 5 and 8 and valleys are at 1 and 3.

Visualization of the Algorithm

Our Algorithm uses 2 ideas to solve this problem:
1. Graph Compression
2. Merging Transactions

We will now be looking at these two steps and how they help in solving our problem

Step 1: Graph Compression

For a brief moment lets forget about the buy and sell stocks question and think about this- Is there a way to compress that zig zag line graph we just saw above? i.e. is there any way to make the graph less zig-zagy while still preserving the information of each transaction? Forget about why we are doing this or how is this relevant for our stocks question for now, everything will be clear soon. Turns out there is a a way to do that. Consider GRAPH 1 that we just saw above. What we can do is we can compress/reduce its zig-zaggyness by converting the graph to this and storing the dip value i.e. 5-3=2 in a variable:

GRAPH 2

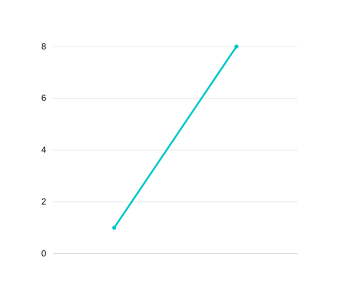
Our new graph is a graph from 1 to 8. If someone were to make a single transaction and obtain max profit then they can just take the 8-1=7 transaction in our compressed graph, which was also the correct answer for our original graph too but what if we are allowed to make 2 transactions? In our original graph we can take (5-1)+(8-3)=9, which can equivalently be written as (8-1)+(5-3). Notice in the second representation the 5-3 part is nothing but the dip value which we had stored in a variable in the compressed graph, so if we want to also bring out the compressed transaction we can just add that variable value. Another example with array [1,10,4,7,6,12]:

GRAPH 3

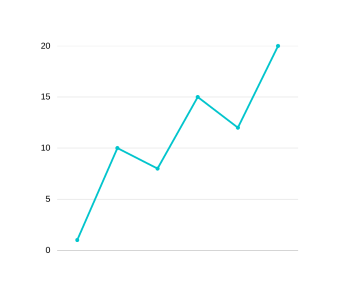
After the first level of compression our original graph will be converted to this with a dip of [3]-

GRAPH 4

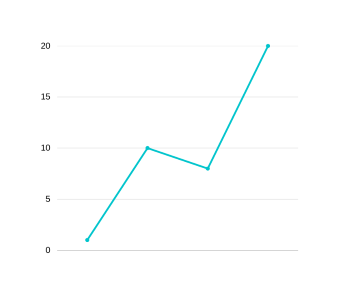
After the second level it will be converted to this with dip [3,2]-

GRAPH 5

The dip values can be stored in a max heap so that we can always obtain the greatest dip. In the end the max heap in our example will have 2 elements [3,2]. Now if we are allowed to make only one transaction then take the final graph mountain and do 20-1=19. If we are allowed to make 2 transactions then take the mountain which gave us 19 and take the max dip available from the heap which in our case is 3. This gives us profit of 19+3=22 which corresponds to the transaction (15-1)+(20-12) in the original graph. If we are allowed to make 3 transaction then take the last remaining dip i.e. 2 and add it to 22 that you had got, thus giving you 22+2=24 which corresponds to (10-1)+(15-8)+(20-12) in the original graph. You see the amazing part of storing these dips is each dip can add an entire transaction all by itself!

Now we are ready to move on to the final piece of our puzzle.

Step 2: Merging Transactions

Hey ayconic! Didn't we just learn to merge transactions in the previous step? Yes we did but that is not the full story. We are still to formally define the conditions for merging and there are also some transactions in the graph that cannot be merged. There are basically 4 kinds of events we would need to look at and decide if they are mergeable or not. They are-

TYPE-I

GRAPH 6

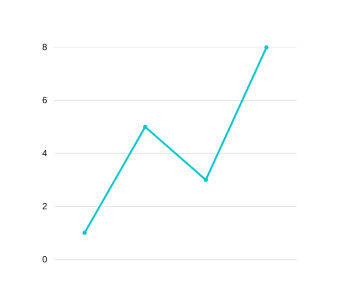
This is the same as graph 1 and can be easily merged as we saw above. Formally if valley-peak pairs are represented by (v1,p1) and (v2,p2) then this condition can be written as: Merge two transactions when v1<v2 and p1<p2.

TYPE-II

GRAPH 7

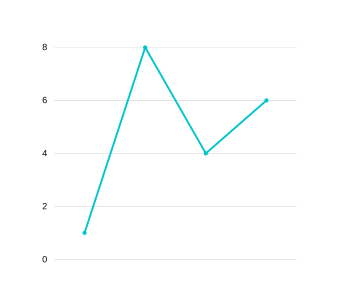
This condition is represented by v1 < v2 and p1 > p2. These cant be merged as of now because remember whenever we merge transactions, the merged graph should represent max profit that can be obtained from a single transaction from the two available ones for the overall algorithm to work. If the graph above is represented by [1,8,4,6] then in our case compressed graph will give 6-1=5 which is wrong as best single transaction is given by 8-1=7. Even tho the graph is not mergeable as of now it can become mergeable later. To see this take a look at the example below-

GRAPH 8

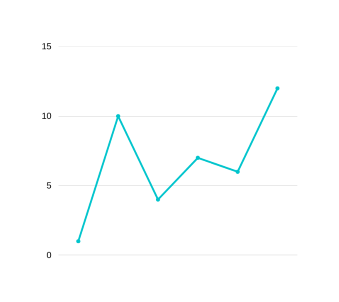
This graph fits well with the array [1,10,4,7,6,12]. Notice that the 1,10,4,7 part represents the TYPE-II graph. Initially that part is not compressable but the part after it is with a dip of 1-

GRAPH 9

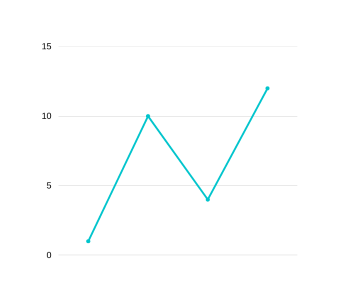
Now as we can see this graph can again be merged now as it has reduced to TYPE-I.

TYPE-III

GRAPH 10

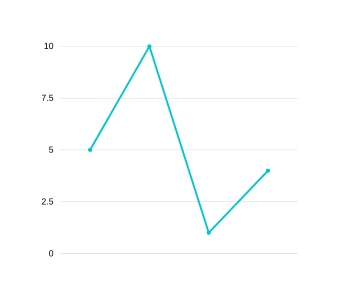
This condition is represented by v1>v2 and p1>p2. Eg- [5,10,1,4] . This graph cannot be made mergeable from the right like we did for TYPE-II. We would need to store this (v1,p1) transaction separately possibly in the dips array by popping it from stack and subsequently all elements in the stack will be popped from top with vi>v2. (v2,p2) will then be kept in stack to check for mergeability and extendability. This point and the functioning of the algorithm will become much clearer after I show you the dry run of the algo, which is just a few lines below. Our algo will be merging whenever it can from the right so there will be no chance of merging from left when we encounter TYPE-III.

TYPE-IV

GRAPH 11

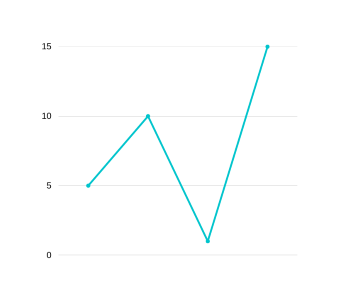
This condition is given by v1>v2 and p1<p2. Eg- [5,10,1,15] . Treatment of this condition is same as TYPE-III.

So in total we have 4 types of possibilities when merging 2 transactions:
1. v1 < v2 and p1 < p2
2. v1 < v2 and p1 > p2
3. v1 > v2 and p1 > p2
4. v1 > v2 and p1 < p2

Dry Run of the Algorithm

Alright! Time to see how all these concepts come together and solve our problem. We will take the array [10,20,15,30,12,25,17,35,5,8,6,12,1,3]. We will be using a stack to store transactions which can be merged immediately or in the future. We will use an array called dips to store the dip values when transactions are merged. For simplicity dips array will not be a heap and instead we will just sort it in the end. The visualization of our array is this-

GRAPH 12

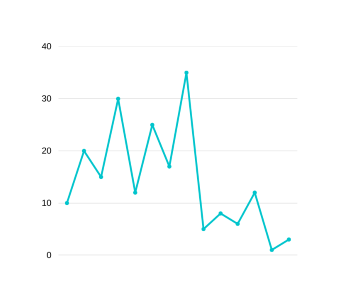
We start from left to right. dips=[],stack=[(10,20)] . Now after discovering (15,30) pair we compare it to top of stack, is it mergeable? Yes so we merge it and store the dip value.

GRAPH 13

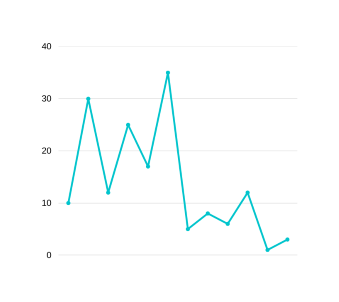
Now, stack=[(10,30)], dips=[5] . Now we move at the next valley peak pair which is (12,25). It is not mergeable but it is type 2 so it may become mergeable from right in the future so we keep it at top of stack. stack=[(10,30),(12,25)], dips=[5] . Our next pair is (17,35) which is mergeable with top of stack so we merge it and obtain-

GRAPH 14

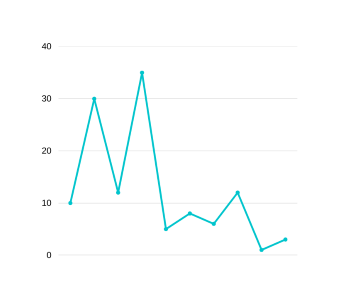
stack=[(10,30),(12,35)],dips=[5,8] . Now since we have extended from right, lets see if top of stack is mergeable with the one just behind it, i.e. if any TYPE-II is waiting just behind it. (12,35) is mergeable with (10,30) so we merge it and obtain-

GRAPH 15

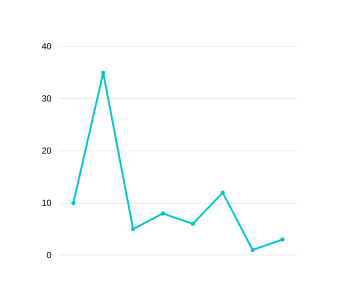
stack=[(10,35)], dips=[5,8,18] . Next pair is (5,8), which is TYPE-III with (10,35) so it can never be merged nor made mergeable from right with (10,35) and hence prevent anything to ever merge with (10,35). So we just pop (10,35) and begin with (5,8). stack=[(5,8)], dips=[5,8,18,25] . Notice that nothing is left extendable as everything is always extended from right. Next pair is (6,12). It is mergeable with top of stack so we get-

GRAPH 16

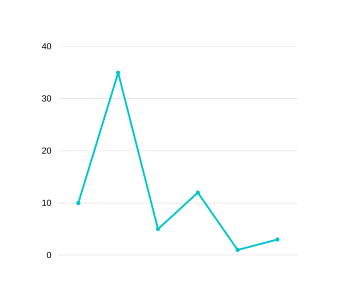
stack=[(5,12)],dips=[5,8,18,25,2] . Final pair is (1,3) which is TYPE-III with (5,12) so we pop (5,12) and since this is end of array we pop (1,3) also to obtain- stack=[], dips=[5,8,18,25,2,7,2] . We then sort dips array to get dips=[25,18,8,7,5,2,2] and we select the first k of them and sum them which will give the max profit one can obtain by doing atmost k transactions. For k>length of dips, just sum the entire dips array and return the answer.