1828A - Divisible Array
Idea: thenymphsofdelphi
Preparation: Mike4235
Remember the sum of the first $$$n$$$ positive integers?
Every positive integer is divisible by $$$1$$$.
Consider the array $$$a = \left[1, 2, \ldots, n\right]$$$ that satisfies the second condition. It has the sum of $$$1 + 2 + \dots + n = \frac{n(n+1)}{2}$$$.
One solution is to notice that if we double every element $$$(a=\left[2, 4, 6, \ldots, 2n\right])$$$, the sum becomes $$$\frac{n(n+1)}{2} \times 2 = n(n + 1)$$$, which is divisible by $$$n$$$.
Another solution is to increase the value of $$$a_1$$$ until the sum becomes divisible by $$$n$$$. This works because every integer is divisible by $$$1$$$, and we only need to increase $$$a_1$$$ by at most $$$n$$$.
Time complexity: $$$\mathcal{O}(n)$$$
#include <bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i = 1; i <= n; i++) cout << i * 2 << " ";
cout << "\n";
}
}
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fi first
#define se second
const int N=2e6+1;
const ll mod=998244353;
ll n,m;
ll a[N],b[N];
void solve(){
cin >> n;
ll s=0;
for(int i=n; i>=2 ;i--){
a[i]=i;
s=(s+i)%n;
}
a[1]=n-s;
for(int i=1; i<=n ;i++) cout << a[i] << ' ';
cout << '\n';
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
int t;cin >> t;
while(t--){
solve();
}
}
1828B - Permutation Swap
Idea: thenymphsofdelphi
Preparation: Mike4235
In order to move $$$p_i$$$ to its right position, what does the value of $$$k$$$ have to satisfy?
In order to move $$$p_i$$$ to position $$$i$$$, it is easy to see that $$$|p_i - i|$$$ has to be divisible by $$$k$$$.
So, $$$|p_1 - 1|, |p_2 - 2|, \ldots, |p_n - n|$$$ has to be all divisible by $$$k$$$. The largest possible value of $$$k$$$ turns out to be the greatest common divisor of integers $$$|p_1 - 1|, |p_2 - 2|, \ldots, |p_n - n|$$$.
Time complexity: $$$\mathcal{O}(n + \log{n})$$$
#include <bits/stdc++.h>
using namespace std;
signed main() {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int t;
cin >> t;
while (t--) {
int n, res = 0;
cin >> n;
for (int i = 1; i <= n; i++) {
int x; cin >> x;
res = __gcd(res, abs(x - i));
}
cout << res << "\n";
}
}
1827A - Counting Orders
Idea: Mike4235
Preparation: thenymphsofdelphi
Sort the array $$$b$$$, and fix the values from $$$a_n$$$ to $$$a_1$$$.
First, we can sort the array $$$b$$$, as it does not change the answer.
Let's try to choose the values of $$$a$$$ from $$$a_n$$$ to $$$a_1$$$. How many ways are there to choose the value of $$$a_i$$$?
The new $$$a_i$$$ must satisfies $$$a_i > b_i$$$. But some of the candidates are already chosen as $$$a_j$$$ for some $$$j > i$$$. However, since $$$a_j > b_j \ge b_i$$$, we know that there are exactly $$$(n - i)$$$ candidates already chosen previously by all values of $$$j > i$$$. So, there are (number of $$$k$$$ such that $$$a_k > b_i$$$) $$$- (n - i)$$$ ways to choose the value of $$$a_i$$$.
We can use two pointers or binary search to efficiently find the (number of $$$k$$$ such that $$$a_k > b_i$$$) for all $$$i$$$.
Time complexity: $$$\mathcal O(n \log n)$$$.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD = 1e9 + 7;
struct testcase{
testcase(){
int n; cin >> n;
vector<int> a(n);
for (int i=0; i<n; i++) cin >> a[i];
sort(a.begin(), a.end());
vector<int> b(n);
for (int i=0; i<n; i++) cin >> b[i];
sort(b.begin(), b.end(), greater<>());
ll result = 1;
for (int i=0; i<n; i++){
int geq_count = a.size() - (upper_bound(a.begin(), a.end(), b[i]) - a.begin());
result = result * max(geq_count - i, 0) % MOD;
}
cout << result << "\n";
}
};
signed main(){
cin.tie(0)->sync_with_stdio(0);
int t; cin >> t;
while (t--) testcase();
}
1827B2 - Range Sorting (Hard Version)
Idea: lanhf
Preparation: Mike4235
What is the minimum cost to sort just one subarray?
What happens when two operations intersect each other?
When can we sort two adjacency ranges independently?
Try to calculate the contribution of each position.
Let $$$a[l..r]$$$ denotes the subarray $$$a_l,a_{l+1},\ldots,a_r$$$.
Observation 1: In an optimal sequence of operations for one subarray, there will be no two operations that intersect each other. In other words, a subarray will be divided into non-overlapping subarrays, and we will apply a range-sort operation to each subarray.
Proof: Suppose there are two operations $$$[l_1,r_1]$$$ and $$$[l_2,r_2]$$$ that intersect each other, we can replace them with one operation $$$[\min(l_1,l_2),\max(r_1,r_2)]$$$ which does not increase the cost.
Observation 2: Consider $$$k$$$ positions $$$l\le i_1<i_2<\ldots < i_k < r$$$, then we can sort subarrays $$$a[l..i_1],$$$ $$$a[i_1+1..i_2],$$$ $$$\ldots,$$$ $$$a[i_k+1..r]$$$ independently iff $$$\max(a[l..i_x])<\min(a[i_x+1..r])$$$ for all $$$1\le x\le k$$$.
Proof: The obvious necessary and sufficient condition required to sort subarrays $$$a[l..i_1],$$$ $$$a[i_1+1..i_2],$$$ $$$\ldots,$$$ $$$a[i_k+1..r]$$$ independently is $$$\max(a[i_{x-1}+1..i_x])<\min(a[i_x+1..i_{x+1}])$$$ for all $$$1\le x\le k$$$, here we denote $$$x_0=l-1$$$ and $$$x_{k+1}=r$$$. It is not hard to prove that this condition is equal to the one stated above.
With these observations, we can conclude that the answer for a subarray $$$a[l..r]$$$ equals the $$$r-l$$$ minus the number of positions $$$k$$$ such that $$$l\le k\lt r$$$ and $$$\max(a[l..k])<\min(a[k+1..r])$$$ $$$(*)$$$. Let us analyze how to calculate the sum of this value over all possible $$$l$$$ and $$$r$$$.
Consider a position $$$i$$$ ($$$1\le i\le n$$$), let's count how many triplets $$$(l, k, r)$$$ satisfy $$$(*)$$$ and $$$min(a[k+1..r]) = a_i$$$. It means that $$$k$$$ must be the closest position to the left of $$$i$$$ satisfying $$$a_k<a_i$$$. Denotes $$$x$$$ as the closest position to the left of $$$k$$$ such that $$$a_x>a_i$$$, and $$$y$$$ as the closest position to the right of $$$i$$$ such that $$$a_y<a_i$$$.
We can see that a triplet $$$(l, k, r)$$$ with $$$x<l\le k$$$ and $$$i\le r<y$$$ will match our condition. In other words, we will add to the answer $$$(k - x) \cdot (y - i)$$$.
In the easy version, we can find such values of $$$x, k, y$$$ for each $$$i$$$ in $$$\mathcal{O}(n)$$$ and end up with a total complexity of $$$O(n^2)$$$. We can further optimize the algorithm by using sparse table and binary lifting and achieve a time complexity of $$$\mathcal{O}(n \log{n})$$$, which is enough to solve the hard version.
There is an $$$\mathcal{O}(n)$$$ solution described here.
#include <bits/stdc++.h>
using namespace std;
const int N = 500005;
const int LOG = 19;
int a[N], r[N], rmq[LOG][N];
void solve() {
int n; cin >> n;
long long res = 0;
vector<int> s;
a[0] = a[n + 1] = 0;
for (int i = 1; i <= n; i++) {
cin >> a[i];
rmq[0][i] = a[i];
res += 1ll * i * (i - 1) / 2;
}
s.push_back(n + 1);
for (int i = n; i > 0; i--) {
while (a[s.back()] > a[i])
s.pop_back();
r[i] = s.back();
s.push_back(i);
}
for (int k = 1; k < LOG; k++)
for (int i = (1 << k); i <= n; i++)
rmq[k][i] = max(rmq[k - 1][i], rmq[k - 1][i - (1 << (k - 1))]);
s.clear();
s.push_back(0);
for (int i = 1; i <= n; i++) {
while (a[s.back()] > a[i])
s.pop_back();
int j = s.back();
for (int k = LOG - 1; k >= 0; k--)
if (j >= (1 << k) && rmq[k][j] < a[i])
j -= 1 << k;
res -= 1ll * (r[i] - i) * (s.back() - j);
s.push_back(i);
}
cout << res << '\n';
}
int main() {
cin.tie(0)->sync_with_stdio(0);
int t; cin >> t;
while (t--) solve();
}
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 5;
int n;
int a[N];
pair <int, int> b[N];
signed main(){
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int tests; cin >> tests; while (tests--){
cin >> n;
for (int i = 1; i <= n; i++){
cin >> a[i];
}
for (int i = 1; i <= n; i++){
b[i] = make_pair(a[i], i);
}
sort(b + 1, b + n + 1);
set <int> sttlo = {0, n + 1}, stthi = {0, n + 1};
for (int i = 1; i <= n; i++){
stthi.emplace(i);
}
long long ans = 0;
for (int len = 1; len <= n; len++){
ans += (long long)(len - 1) * (n - len + 1);
}
for (int i = 1; i <= n; i++){
int idx = b[i].se;
stthi.erase(idx); sttlo.emplace(idx);
int x2 = *stthi.lower_bound(idx);
int x1 = *prev(stthi.lower_bound(idx));
if (x2 == n + 1){
continue;
}
int x3 = *sttlo.lower_bound(x2);
ans -= (long long)(idx - x1) * (x3 - x2);
}
cout << ans << endl;
}
}
Solve the problem when the beauty of an array is (minimum time needed to sort)$$$^2$$$.
1827C - Palindrome Partition
Idea: lanhf
Preparation: lanhf
Try to construct beautiful string greedily.
What happens when we have two even palindromes share one of their endpoints?
For the simplicity of the solution, we will abbreviate even palindrome as evp.
Lemma: Consider a beautiful string $$$t$$$, we can find the unique maximal partition for it by greedily choosing the smallest possible evp in each step from the left. Here maximal means maximum number of parts.
Proof: Suppose $$$t[0..l)$$$ is smallest prefix which is an evp and $$$t[0..r)$$$ is the first part in the partition of $$$t$$$, here $$$t[l..r)$$$ mean substring $$$t_l t_{l+1}\ldots t_{r-1}$$$. We consider two cases:
- $$$2l\le r$$$: In this case, it is clear that $$$t[0..l)$$$, $$$t[l..r - l)$$$ and $$$t[r-l..r)$$$ are evps, so we can replace $$$t[0..r)$$$ with them.

- $$$2l>r$$$: In this case, due to the fact that $$$t[r-l..l)$$$ and $$$t[0..l)$$$ are evps, $$$t[0..2l-r)$$$ is also an evp, which contradicts to above assumption that $$$t[0..l)$$$ is the smallest.

We can use dynamic programming to solve this problem. Let $$$dp_i$$$ be the number of beautiful substrings starting at $$$i$$$. For all $$$i$$$ from $$$n-1$$$ to $$$0$$$, if there are such $$$next_i$$$ satisfying $$$s[i..next_i)$$$ is the smallest evp beginning at $$$i$$$, then $$$dp_i=dp_{next_i}+1$$$, otherwise $$$dp_i=0$$$. The answer will be the sum of $$$dp_i$$$ from $$$0$$$ to $$$n-1$$$.
To calculate the $$$next$$$ array, first, we use Manacher algorithm or hashing to find the maximum $$$pal_i$$$ satisfying $$$s[i-pal_i..i+pal_i)$$$ is an evp for each $$$i$$$. Then for all $$$0\le i< n$$$, $$$next_i=2j-i$$$ where $$$j$$$ is smallest position such that $$$i<j$$$ and $$$j-pal_j\le i$$$. The time complexity is $$$\mathcal{O}(n \log{n})$$$.
#include <bits/stdc++.h>
using namespace std;
const int N = 500005;
const int LOG = 19;
int n, pal[N], rmq[LOG][N], cnt[N];
string s;
int main() {
cin.tie(0)->sync_with_stdio(0);
int t; cin >> t;
while (t--) {
cin >> n >> s;
for (int i = 0, l = 0, r = 0; i < n; i++) {
pal[i] = i >= r ? 0 : min(pal[l + r - i], r - i);
while (i + pal[i] < n && i - pal[i] - 1 >= 0
&& s[i + pal[i]] == s[i - pal[i] - 1]) pal[i]++;
if (i + pal[i] > r) {
l = i - pal[i]; r = i + pal[i];
}
}
for (int i = 0; i < n; i++)
rmq[0][i] = i - pal[i];
for (int k = 1; k < LOG; k++)
for (int i = 0; i + (1 << k) <= n; i++)
rmq[k][i] = min(rmq[k - 1][i],
rmq[k - 1][i + (1 << (k - 1))]);
for (int i = 1; i <= n; i++)
cnt[i] = 0;
for (int i = 0; i < n; i++) {
int j = i + 1;
for (int k = LOG - 1; k >= 0; k--)
if (j + (1 << k) <= n && rmq[k][j] > i)
j += 1 << k;
if (2 * j - i <= n)
cnt[2 * j - i] += cnt[i] + 1;
}
long long res = 0;
for (int i = 1; i <= n; i++)
res += cnt[i];
cout << res << '\n';
}
}
Solve the problem in $$$\mathcal{O}(n)$$$.
1827D - Two Centroids
Idea: Mike4235
Preparation: lanhf
Is the answer related to the centroid of the current tree?
How much the centroid will move after one query?
Observation: The answer for the tree with $$$n$$$ vertices equals $$$n-2\cdot mx$$$ where $$$mx$$$ is the largest subtree among the centroid's children.
Lemma: After one query, the centroid will move at most one edge, and when the centroid move, the tree before the query already has two centroids.
Proof:
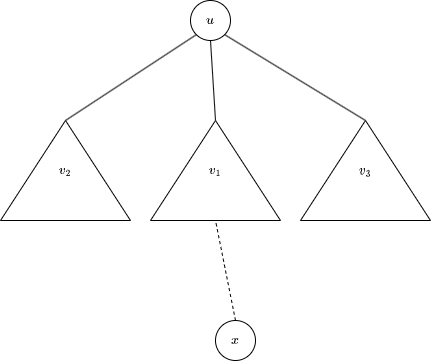
Suppose the tree before the query has $$$n$$$ vertices and the current centroid is $$$u$$$. Let $$$v_1, v_2,\ldots,v_k$$$ are the children of $$$u$$$ and the next query vertex $$$x$$$ is in subtree $$$v_1$$$. Clearly, the centroid is either $$$u$$$ or in the subtree $$$v_1$$$. Consider the latter case, because the size of subtree $$$v_1$$$ does not greater than $$$\lfloor \frac{n}{2}\rfloor$$$, the size of newly formed subtree including $$$u$$$ is greater or equal to $$$\lceil \frac{n}{2}\rceil$$$. Moving one or more edges away from $$$v_1$$$ will increase the size of this new subtree by one or more, and the vertex can not become centroid because $$$\lceil \frac{n}{2}\rceil+1>\lfloor \frac{n+1}{2}\rfloor$$$.
The second part is easy to deduce from the above proof.
We will solve this problem offline. First, we compute the Euler tour of the final tree and use "range add query" data structures like Binary indexed tree (BIT) or Segment tree to maintain each subtree's size. We will maintain the size of the largest subtree among the centroid's children $$$mx$$$. In the case where the centroid does not move, we just update $$$mx$$$ with the size of the subtree including the newly added vertex, otherwise, we set $$$mx$$$ to $$$\lfloor \frac{n}{2}\rfloor$$$ due to the lemma. The time complexity is $$$\mathcal{O}(n \log{n})$$$.
#include <bits/stdc++.h>
using namespace std;
const int N = 500005;
const int LOG = 19;
vector<int> adj[N];
int tin[N], tout[N], timer;
int par[LOG][N], bit[N], dep[N];
void dfs(int u) {
tin[u] = ++timer;
dep[u] = dep[par[0][u]] + 1;
for (int k = 1; k < LOG; k++)
par[k][u] = par[k - 1][par[k - 1][u]];
for (int v : adj[u]) dfs(v);
tout[u] = timer;
}
void add(int u) {
for (int i = tin[u]; i < N; i += i & -i)
bit[i]++;
}
int get(int u) {
int res = 0;
for (int i = tout[u]; i > 0; i -= i & -i)
res += bit[i];
for (int i = tin[u] - 1; i > 0; i -= i & -i)
res -= bit[i];
return res;
}
int jump(int u, int d) {
for (int k = 0; k < LOG; k++)
if (d >> k & 1) u = par[k][u];
return u;
}
bool cover(int u, int v) {
return tin[u] <= tin[v] && tin[v] <= tout[u];
}
void solve() {
int n; cin >> n;
/// reset
timer = 0;
for (int i = 1; i <= n; i++) {
bit[i] = 0; adj[i].clear();
}
for (int i = 2; i <= n; i++) {
cin >> par[0][i];
adj[par[0][i]].push_back(i);
}
dfs(1); add(1);
int cen = 1, max_siz = 0;
for (int u = 2; u <= n; u++) {
add(u);
if (cover(cen, u)) {
int v = jump(u, dep[u] - dep[cen] - 1);
int siz = get(v);
if (siz >= (u + 1) / 2) {
cen = v; max_siz = u / 2;
} else max_siz = max(max_siz, siz);
} else {
int siz = get(cen);
if (siz < (u + 1) / 2) {
cen = par[0][cen]; max_siz = u / 2;
} else max_siz = max(max_siz, u - siz);
}
cout << u - 2 * max_siz << " \n"[u == n];
}
}
int main() {
cin.tie(0)->sync_with_stdio(0);
int t; cin >> t;
while (t--) solve();
}

1827E - Bus Routes
Idea: Mike4235
Preparation: thenymphsofdelphi
You do not need to consider all pairs of nodes, only some of them will do.
Find an equivalent condition of the statement.
Let $$$S(u)$$$ be the set of all nodes reachable by u using at most one route. Consider all $$$S(l)$$$ where $$$l$$$ is a leaf in the tree.
First, notice that for a pair of nodes $$$(u, v)$$$ such that $$$u$$$ is not a leaf, we can find a leaf $$$l$$$ such that path $$$(l, v)$$$ fully covers path $$$(u, v)$$$. Therefore, we only need to care about whether all pairs of leaves can reach each other using at most $$$2$$$ routes.
Lemma
The condition above is equivalent to: There exists a node $$$c$$$ such that $$$c$$$ can reach all leaves by using at most one route.
Proof
The necessity part is trivial, so let's prove the sufficiency part.
Let the leaves of the tree be $$$l_1, l_2, \ldots, l_m$$$.
Let $$$S(u)$$$ be the induced subgraph of all nodes reachable by $$$u$$$ using at most one route. If $$$u$$$ and $$$v$$$ is reachable within two routes, then the intersection of $$$S(v)$$$ and $$$S(u)$$$ is non-empty. We need to prove that the intersection of all $$$S(l_i)$$$ is non-empty.
If $$$l_i$$$, $$$l_j$$$, and $$$l_k$$$ are pairwise reachable within two paths, then the intersection of $$$S(l_i)$$$, $$$S(l_j)$$$, and $$$S(l_k)$$$ must be pairwise non-empty. Since the graph is a tree, it follows trivially that intersection of $$$S(l_i)$$$, $$$S(l_j)$$$, and $$$S(l_k)$$$ must be non-empty. We can generalize this to all leaves, thus proving the sufficiency part.
To check if an answer exists or not, we can use this trick from ko_osaga to find how many $$$S(l_i)$$$ covers each node in $$$\mathcal O(n)$$$. The answer is YES when there is a node $$$c$$$ that is covered by all $$$S(l_i)$$$.
To find the two candidates when the answer is NO, notice that one of them is the first leaf $$$l_x$$$ such that there is no node $$$c$$$ that is covered by $$$S(l_1), \ldots, S(l_x)$$$. We can find $$$l_x$$$ with binary search. To find the other one, root the tree at $$$l_x$$$ and define $$$lift_u$$$ as the lowest node reachable by $$$u$$$ using at most one route. The other candidate is a node $$$l_y$$$ such that $$$lift_{l_y}$$$ is not in $$$S(l_x)$$$.
Time complexity: $$$\mathcal O(n \log n)$$$.
Tester's solution: Root the tree at some non-leaf vertex. Define $$$lift_u$$$ as the lowest node (minimum depth) reachable by $$$u$$$ using at most one route. Take the node $$$v$$$ with the deepest (maximum depth) $$$lift_v$$$. Then the answer for this problem is $$$\texttt{YES}$$$ iff for every leaf $$$l$$$, either $$$l$$$ lie in $$$lift_v$$$ 's subtree or $$$l$$$ has a path to $$$lift_v$$$.
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
const int LOG = 19;
/// lca stuff
int tin[N], timer = 0;
vector<int> path, rmq[LOG];
/// some tree stuff
vector<int> adj[N], leaf, topo;
int n, m, par[N], val[N];
/// trips
vector<int> trip[N];
void dfs_pre(int u) {
topo.push_back(u);
tin[u] = timer++;
for (int v : adj[u])
if (v != par[u]) {
path.push_back(u);
rmq[0].push_back(tin[u]);
par[v] = u; dfs_pre(v);
}
}
int get_min(int l, int r) {
int k = 31 - __builtin_clz(r - l);
return min(rmq[k][l], rmq[k][r - (1 << k)]);
}
int lca(int u, int v) {
if (u == v) return u;
tie(u, v) = minmax(tin[u], tin[v]);
return path[get_min(u, v)];
}
int lca_reroot(int r, int u, int v) {
return lca(r, u) ^ lca(r, v) ^ lca(u, v);
}
void calc_val() {
for (int u : topo)
for (int v : adj[u])
if (v != par[u]) val[u] += val[v];
}
void add(int u) {
for (int v : trip[u])
if (v < 0) val[-v]--;
else val[v]++;
}
bool check(int l) {
for (int u = 1; u <= n; u++) val[u] = 0;
for (int i = 0; i < l; i++) add(leaf[i]);
calc_val();
for (int u = 1; u <= n; u++)
if (val[u] == l) return true;
return false;
}
void solve() {
cin >> n >> m;
/// reset
for (int i = 1; i <= n; i++) {
adj[i].clear(); trip[i].clear();
}
timer = 0; leaf.clear(); topo.clear();
path.clear(); rmq[0].clear();
for (int i = 1; i < n; i++) {
int u, v; cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
/// leaves only
for (int i = 1; i <= m; i++) {
int u, v; cin >> u >> v;
if (adj[u].size() == 1)
trip[u].push_back(v);
if (adj[v].size() == 1)
trip[v].push_back(u);
}
if (n == 1) {
cout << "YES\n"; return;
}
/// prepare
dfs_pre(1);
reverse(topo.begin(), topo.end());
for (int k = 1; (1 << k) <= n; k++) {
rmq[k].resize(n - (1 << k) + 1);
for (int i = 0; i + (1 << k) <= n; i++)
rmq[k][i] = min(rmq[k - 1][i],
rmq[k - 1][i + (1 << (k - 1))]);
}
for (int u = 1; u <= n; u++)
if (adj[u].size() == 1) {
leaf.push_back(u);
trip[u].push_back(u);
sort(trip[u].begin(), trip[u].end(),
[&](int x, int y) {
return tin[x] < tin[y];});
int l = trip[u].size();
for (int i = 0; i + 1 < l; i++)
trip[u].push_back(-lca
(trip[u][i], trip[u][i + 1]));
trip[u].push_back(-par[lca
(trip[u][0], trip[u][l - 1])]);
}
/// find longest prefix of leaves
int l = 0;
for (int k = LOG - 1; k >= 0; k--)
if (l + (1 << k) <= leaf.size()
&& check(l + (1 << k))) l += 1 << k;
if (l == leaf.size()) {
cout << "YES\n"; return;
}
cout << "NO\n";
for (int u = 1; u <= n; u++) val[u] = 0;
add(leaf[l]); calc_val();
for (int u : leaf) {
bool good = false;
for (int v : trip[u]) {
if (v <= 0) break;
if (val[lca_reroot(leaf[l], u, v)]) {
good = true; break;
}
}
if (!good) {
cout << leaf[l] << ' ' << u << '\n';
return;
}
}
}
int main() {
cin.tie(0)->sync_with_stdio(0);
int t; cin >> t;
while (t--) solve();
}
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll INF = 1e18;
const int maxn = 2e6 + 10;
const int mod = 1e9 + 7;
const int mo = 998244353;
using pi = pair < ll, ll > ;
using vi = vector < ll > ;
using pii = pair < pair < ll, ll > , ll > ;
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
vector < int > G[maxn];
int n, m;
int h[maxn];
int eu[maxn];
pair < int, int > rmq[maxn][21];
int l = 0;
int st[maxn];
int out[maxn];
int low[maxn];
pair < int, int > ed[maxn];
int par[maxn];
int ok[maxn];
int d[maxn];
void dfs(int u, int pa) {
eu[++l] = u;
st[u] = l;
for (auto v: G[u]) {
if (v == pa) continue;
par[v] = u;
h[v] = h[u] + 1;
dfs(v, u);
eu[++l] = u;
}
out[u] = l;
}
void init() {
for (int j = 1; (1 << j) <= l; j++) {
for (int i = 1; i <= l; i++) {
rmq[i][j] = min(rmq[i][j - 1], rmq[i + (1 << (j - 1))][j - 1]);
}
}
}
int LCA(int u, int v) {
if (st[u] > st[v]) {
swap(u, v);
}
int k = log2(st[v] - st[u] + 1);
return min(rmq[st[u]][k], rmq[st[v] - (1 << k) + 1][k]).second;
}
bool check(int u, int pa, int c) {
if (st[pa] <= st[c] && st[c] <= out[pa]) {
if (st[c] <= st[u] && st[u] <= out[c]) {
return true;
}
return false;
}
return false;
}
void solve() {
cin >> n >> m;
l = 0;
for (int i = 1; i <= n; i++) {
G[i].clear();
}
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
G[x].push_back(y);
G[y].push_back(x);
}
dfs(1, -1);
for (int i = 1; i <= l; i++) {
rmq[i][0] = {st[eu[i]], eu[i]};
}
init();
for (int i = 1; i <= n; i++) {
low[i] = i;
ok[i] = 0;
}
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
ed[i] = {x, y};
int u = LCA(x, y);
if (h[low[x]] > h[u]) {
low[x] = u;
}
if (h[low[y]] > h[u]) {
low[y] = u;
}
}
int need = 0;
for (int i = 2; i <= n; i++) {
if (low[i] != 1 && G[i].size() == 1) {
if (need == 0 || h[low[need]] < h[low[i]]) {
need = i;
}
}
}
if (need == 0) {
cout << "YES\n";
return;
}
for (int i = 1; i <= m; i++) {
int u = LCA(ed[i].first, ed[i].second);
if (G[ed[i].first].size() == 1 && check(ed[i].second, u, low[need])) {
ok[ed[i].first] = 1;
}
if (G[ed[i].second].size() == 1 && check(ed[i].first, u, low[need])) {
ok[ed[i].second] = 1;
}
}
for (int i = 1; i <= n; i++) {
if (G[i].size() == 1) {
if (st[low[need]] <= st[i] && st[i] <= out[low[need]]) {
continue;
}
if (ok[i] == 0) {
cout << "NO\n";
cout << need << " " << i << "\n";
return;
}
}
}
cout << "YES\n";
return;
}
signed main() {
cin.tie(0), cout.tie(0) -> sync_with_stdio(0);
int t;
cin >> t;
while (t--) solve();
return 0;
}

1827F - Copium Permutation
Idea: lanhf
Preparation: lanhf
Solve the problem for fixed $$$k$$$
Call the last $$$n-k$$$ elements as special numbers.
Observation: In optimal rearrangement, every maximal segment of special numbers will be placed on consecutive positions in either ascending order or descending order. For simplicity, from now on we will call maximal segment of special number as maximal segment.
For example, take a permutation $$$p=[7, 5, 8, 1, 4, 2, 6, 3]$$$ and $$$k=2$$$, the maximal segments are $$$[1, 4]$$$, $$$[6, 6]$$$ and $$$[8, 8]$$$.
We divide the set of copium subarrays into three parts, one for those lie entirely on prefix $$$p[1..k]$$$, one for those lie entirely on suffix $$$p[k+1..n]$$$, and one for the rest. The number of subarrays in the first part can be calculated with the algorithm used in 526F - Pudding Monsters. The number of subarrays in the second part can be easily deduced from above observation.
Define an array $$$good=[good_1,good_2,\ldots,good_m]$$$ such that for each $$$i$$$: $$$good_i<good_{i+1}$$$ and subarray $$$p[good_i..k]$$$ contains consecutive nonspecial numbers.
For example, take a permutation $$$p=[1, 5, 4,3,7,8,9,2,10,6]$$$ and $$$k=5$$$, then $$$good=[1, 4, 5]$$$.
We will process $$$good$$$ array from right to left while adding special numbers from left to right. Let us consider $$$good_i$$$, first add all special numbers which are missing from subarray $$$[good_i, k]$$$ at the end of current permutation. If $$$[good_i, k]$$$ is not already copium, we increase our answer by one. Denote $$$mn_i$$$ and $$$mx_i$$$ as the minimum and maximum number in subarray $$$[good_i, k]$$$. Loot at two maximal segments, one contains $$$mn_i-1$$$ and one contains $$$mx_i+1$$$. We can place them here to increase the answer.
For example, let $$$n=10$$$, $$$k=5$$$, $$$good_i=3$$$ and the current permutation $$$p=[1, 10, 4, 5, 7, 6]$$$. The two maximal segments are $$$[2, 3]$$$ and $$$[8, 9]$$$. We can place them like $$$[1, 10, 4, 5, 7, 6, 8, 9, 3, 2]$$$ to increase the answer by 4. Furthermore, we can see that three good positions $$$3$$$, $$$4$$$ and $$$5$$$ benefit from maximal segment $$$[8, 9]$$$. In general, consider consecutive good positions $$$good_i, good_{i+1},\ldots, good_j$$$ satisfying $$$mx_i=mx_{i+1}=\ldots=mx_j$$$, all of them can benefit from the same maximal segment if for all $$$i\le x< j$$$, subarray $$$[good_x..good_{x+1}-1]$$$ is copium $$$(*)$$$.
There is a similar condition when we consider consecutive good positions having the same $$$mn$$$. So the algorithm goes like this: For each value of $$$mn$$$ and $$$mx$$$, find the longest segment of good positions satisfying condition $$$(*)$$$, then multiply with the length of corresponding maximal segment and add to the answer.
Solve for each $$$k$$$
We will calculate the answer for each $$$k$$$ from $$$0$$$ to $$$n$$$ in this order. We will store the longest segment for each prefix of $$$mn$$$-equivalent and $$$mx$$$-equivalent positions. Note that when going from $$$k-1$$$ to $$$k$$$, only a suffix of $$$good$$$ will no longer be good, so we can manually delete them one by one from right to left, then add $$$k$$$. There will be at most $$$2$$$ good positions we need to consider. The first one, of course, is $$$k$$$. If $$$p_{k-1}<p_k$$$ or $$$p_{k-1}>p_k$$$, let $$$j$$$ be the last position satisfying $$$p_j>p_k$$$ or $$$p_j<p_k$$$, the second one is the first good position after $$$j$$$ and it satisfies a property: It must be the last position in the $$$mn$$$-equivalent or $$$mx$$$-equivalent positions. The proof is left as an exercise. Therefore, updating this position will not affect the positions behind it. The overall complexity is $$$\mathcal{O}(n\log n)$$$.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 200005;
const int LOG = 18;
int n, a[N], pos[N];
int lef[N], rig[N];
vector<int> st_max, st_min;
void connect(int x, int y) {
rig[x] = y; lef[y] = x;
}
struct range_min {
vector<int> spt[LOG];
void build() {
for (int k = 0; k < LOG; k++)
spt[k].resize(n + 1);
for (int i = 1; i <= n; i++)
spt[0][i] = pos[i];
for (int k = 1; k < LOG; k++)
for (int i = 1; i + (1 << k) <= n + 1; i++) {
spt[k][i] = min(spt[k - 1][i],
spt[k - 1][i + (1 << (k - 1))]);
}
}
int get_min_pos(int l, int r) {
int k = __lg(r - l + 1);
return min(spt[k][l], spt[k][r - (1 << k) + 1]);
}
} rmq;
int get_min(int i) {
return a[*lower_bound(st_min.begin(), st_min.end(), i)];
}
int get_max(int i) {
return a[*lower_bound(st_max.begin(), st_max.end(), i)];
}
struct segtree1 {
#define il i * 2
#define ir i * 2 + 1
struct node {
int val, cnt, tag;
};
node tree[N * 4];
void build(int i, int l, int r) {
tree[i] = {l, 1, 0};
if (l < r) {
int m = (l + r) / 2;
build(il, l, m);
build(ir, m + 1, r);
}
}
void add(int i, int l, int r, int x, int y, int v) {
if (l >= x && r <= y) {
tree[i].val += v; tree[i].tag += v; return;
}
int m = (l + r) / 2;
if (m >= x) add(il, l, m, x, y, v);
if (m < y) add(ir, m + 1, r, x, y, v);
tree[i].val = tree[il].val;
tree[i].cnt = tree[il].cnt;
if (tree[i].val > tree[ir].val) {
tree[i].val = tree[ir].val;
tree[i].cnt = tree[ir].cnt;
} else if (tree[i].val == tree[ir].val)
tree[i].cnt += tree[ir].cnt;
tree[i].val += tree[i].tag;
}
#undef il
#undef ir
} seg1;
struct copium {
int curr, maxx, type;
copium() {}
copium(int curr, int maxx, int type):
curr(curr), maxx(max(maxx, curr)), type(type) {}
};
copium lmin[N], lmax[N];
ll prefix, middle, suffix;
/// cancer
void calc(int i, int j, bool recalc) {
int imin = get_min(i), imax = get_max(i);
int jmin = get_min(j), jmax = get_max(j);
int type;
if (recalc) {
middle -= 1ll * lmax[j].maxx * (rig[jmax] - jmax - 1);
middle -= 1ll * lmin[j].maxx * (jmin - lef[jmin] - 1);
}
if (imax == jmax) {
if (!recalc)
middle -= 1ll * lmax[i].maxx * (rig[imax] - imax - 1);
if (jmin - imin == j - i) type = 0;
else if (imin + j - i == lef[jmin] + 1) type = 1;
else type = 2;
if (type == 2) lmax[j] = copium(1, lmax[i].maxx, type);
else if (lmax[i].type == 0)
lmax[j] = copium(lmax[i].curr + 1, lmax[i].maxx, type);
else lmax[j] = copium(2, lmax[i].maxx, type);
} else lmax[j] = {1, 1, 3};
if (imin == jmin) {
if (!recalc)
middle -= 1ll * lmin[i].maxx * (imin - lef[imin] - 1);
if (imax - jmax == j - i) type = 0;
else if (imax + i - j == rig[jmax] - 1) type = 1;
else type = 2;
if (type == 2) lmin[j] = copium(1, lmin[i].maxx, type);
else if (lmin[i].type == 0)
lmin[j] = copium(lmin[i].curr + 1, lmin[i].maxx, type);
else lmin[j] = copium(2, lmin[i].maxx, type);
} else lmin[j] = {1, 1, 3};
middle += 1ll * lmax[j].maxx * (rig[jmax] - jmax - 1);
middle += 1ll * lmin[j].maxx * (jmin - lef[jmin] - 1);
}
int main() {
cin.tie(0)->sync_with_stdio(0);
int t; cin >> t;
while (t--) {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i]; pos[a[i]] = i;
lef[i] = rig[i] = 0;
}
st_min.assign(1, 0);
st_max.assign(1, 0);
set<int> sorted;
sorted.insert(0);
sorted.insert(n + 1);
prefix = 0;
suffix = 1ll * n * (n + 1) / 2;
middle = 0;
// k = 0
cout << suffix << ' ';
lef[n] = 0; rig[0] = n;
seg1.build(1, 1, n); rmq.build();
vector<int> good;
for (int i = 1; i <= n; i++) {
while (good.size()) {
int j = good.back();
int jmin = get_min(j), jmax = get_max(j);
if (rmq.get_min_pos(min(jmin, a[i]), max(jmax, a[i])) < j) {
middle -= 1ll * lmax[j].maxx * (rig[jmax] - jmax - 1);
middle -= 1ll * lmin[j].maxx * (jmin - lef[jmin] - 1);
good.pop_back();
if (good.size()) {
if (lmax[j].type < 3)
middle += 1ll * lmax[good.back()].maxx * (rig[jmax] - jmax - 1);
if (lmin[j].type < 3)
middle += 1ll * lmin[good.back()].maxx * (jmin - lef[jmin] - 1);
}
} else break;
}
if (good.size()) {
int j = good.back();
int jmin = get_min(j), jmax = get_max(j);
middle -= 1ll * lmax[j].maxx * (rig[jmax] - jmax - 1);
middle -= 1ll * lmin[j].maxx * (jmin - lef[jmin] - 1);
}
auto it = sorted.upper_bound(a[i]);
suffix -= 1ll * (*it - a[i]) * (a[i] - *prev(it));
connect(*prev(it), a[i]); connect(a[i], *it);
sorted.insert(a[i]);
while (st_max.size() > 1 && a[st_max.back()] < a[i]) {
seg1.add(1, 1, n, st_max[st_max.size() - 2] + 1,
st_max.back(), a[i] - a[st_max.back()]);
st_max.pop_back();
}
while (st_min.size() > 1 && a[st_min.back()] > a[i]) {
seg1.add(1, 1, n, st_min[st_min.size() - 2] + 1,
st_min.back(), a[st_min.back()] - a[i]);
st_min.pop_back();
}
st_max.push_back(i); st_min.push_back(i);
if (good.size()) {
int j = good.back();
int jmin = get_min(j), jmax = get_max(j);
middle += 1ll * lmax[j].maxx * (rig[jmax] - jmax - 1);
middle += 1ll * lmin[j].maxx * (jmin - lef[jmin] - 1);
calc(j, i, 0);
} else {
lmax[i] = lmin[i] = {1, 1, 3};
middle += rig[a[i]] - lef[a[i]] - 2;
}
good.push_back(i);
if (st_min.size() >= 2) {
int k = upper_bound(good.begin(), good.end(),
st_min[st_min.size() - 2]) - good.begin();
if (k > 0 && k < good.size())
calc(good[k - 1], good[k], 1);
}
if (st_max.size() >= 2) {
int k = upper_bound(good.begin(), good.end(),
st_max[st_max.size() - 2]) - good.begin();
if (k > 0 && k < good.size())
calc(good[k - 1], good[k], 1);
}
cout << prefix + good.size() + middle + suffix << ' ';
prefix += seg1.tree[1].cnt;
}
cout << '\n';
}
}










fast editorial!
I was waiting for it
Lots of solutions for Problem A. You can also observe that sum(1..N) % N is 0 if N is odd, and N/2 if N is even, so you can construct A=1..N if N is odd, and when N is even it's the same except you change A[N/2] = N.
Here's another one, similar to yours but without odd/even check:
[n - (sum(2..n)%n), 2, ..., n]Hi, relatively new here, probably have a dumb question. Coding in python like a real noob. Can anyone explain to me a detail from problem 3, Counting orders. This part of the code specifically.
for i in range(n):; while j < n and a[i] > b[j]:; j += 1; ans = (ans * (j — i)) % int(1e9 + 7); print(ans)
why can't we just write print(ans % int(1e9 + 7) in the last line without having to calculate ans = (ans * (j — i)) % int(1e9 + 7) each iteration? im guessing because ans probably gets too large, right?
Well integer have no limits in python, but when they become big (in this case too big), they will slow down the calculation (calculation with numbers that take less space in memory is faster), which is way you should always apply the mod after each step.
I solved D1B1 using DSU, if we fix the start of the subarray we can keep adding an element and find its position in the new sorted array with DSU.
submission link: https://mirror.codeforces.com/contest/1828/submission/205880043
Is it possible to optimize this idea to pass B2
Can you please explain the idea or give any similar problem which uses the same idea?
We divide the current array into non-overlapping subarrays as the editorial, but we also visualise them as connected components (cost of a component is the size-1, minimum time is the sum of costs of all components).
If we know the connected components of a subarray [L,R-1] then we can find the subarray [L,R] by finding the leftmost component k such that it has a value > a[R], and then connecting R with k and every component after it so after sorting that component R will be in its correct position.
Can you please tell me what these lines of code are doing?
Thanks
Upd: Got it. Thanks
We assume that the subarray [L,R-1] is already sorted, then we just need to add R by shifting the elements greater than a[R] after it, so they have to be in the same connected component as R.
Can u explain the time complexity for the inner while loop(amortised ananlysis) ? Worst case O(n)?
The while loop must stop when there is only one component left (
j - sz[get(j)] >= iis true when there are more than one component), and every iteration the number of components decreases by $$$1$$$. So for each $$$i$$$, the total number of iterations is at most $$$n - i$$$.Thanks with a upvote
Typo in Range sorting
We can see that a triplet (l,k,r) with x<l≤k and i≤r<y will match our condition.
I fixed that. Thanks.
Div2.C and Div2.D have the same points.But why is D much more difficult than C?
Maybe it's because there are two versions of this problem.
For the C bonus:
The only part in the editorial solution that is $$$O(n \log(n))$$$ is the sparse table for finding the minimum length prefix palindrome. This step can be done in $$$O(n)$$$ total instead. Going right to left, we can add the even palindromes with centre at $$$i$$$ to a stack. Now the potentially smallest palindrome is at the top of the stack. So the stack can be popped from, while the palindrome at the top of the stack does not reach far enough. Then the topmost palindrome on the stack must be the minimum prefix palindrome. This is $$$O(n)$$$ amortized.
My submission: 205927403 (I thought instead of removing suffix palindromes, but the logic is equivalent, only reversed)
Also can use PAM instead.
What's the full form of PAM?
https://www.geeksforgeeks.org/palindromic-tree-introduction-implementation/
I think we can use 2 stacks for B2, which is $$$O(n)$$$. https://mirror.codeforces.com/contest/1828/submission/205931557
Hey, can you explain your intuition and what your code does it would be very helpful
It is the same as in editorial. I just optimize the process finding $$$x,k,y$$$. The first stack is to record $$$k$$$ and the second is to record $$$x$$$.
Nice solution!
I couldn't come up with this approach in contest. Thanks for a clever solution!
I kinda fucked up D. I knew how to find moving centroids, but for some reason I came up with wrong methods to find maximum size subtree there. So I just gave up and used Top tree to find maximum size subtree of given node. Code
In retrospect either I should not be dumb or I should try to cheese with top trees in the first place
all the best for next time :) .
Cannot pass Div2 D1 with BIT+Seg unless replacing seg with vector :( .
Div2.D1 was equally hard as normal D, then why there is no separate editorial for it ? I want to know how to do it in O ( N ^ 2 ).
If you made two separate problems, then please write two separate editorials for both the problems ( or at least explain something ) .
downvoting for not explaining D1 clearly.
Wow man really just saw the headings, and didnt even bother to read. Look prperly.
I have read it, including the bonus problem where beauty is ( square of min cost ) . not that I can solve that xD
Then why are you complaining? If you read it, you qould see the editorial has nearly same sols for easy and hard version. Why would they make 2 separate editorials when they do not explain anything new.
But in the last paragraph the author has mentioned about the solution of D1.
that's true. they have mentioned, but I am not able to understand last 2-3 para's of editorial. I made a mistake by not reading last para clearly. but even after reading it , I am not able to understand clearly.
it is D1' solution as well. According to the editoral the only difference between D1 and D2 is the last paragraph.
If you don't use sparse table or something like that,you will do it in O(N^2)
I have a puzzle question, for example 4 and 2, 1, 4, 3, why is the answer 6
can someone explain why (k-x) * (y-i) is added to answer in Div2D1 ?
Till para 5, it says that for each [ l ... r ] ( 1 <= l < n , l < r <= n ) , we will find number of 'k's such that each max(a[l...k]) < min(a[k+1...r).
So, based on this assumption, we would think that
After this, logic changes on para 6, for each 'i', lets find first left index, which is less that a[i] , lets call that
index 'k'. ( a[k] < a[i] )
Now, find first index on the left side of 'k' which is greater than a[i], lets call this index 'x' , ( a[x] > a[i] )
Now, find first index on the right side of 'i' which is less than a[i], lets call this index 'y' , (a[y] < a[i] )
so, putting this in code,
But why are we adding this (k-x) * (y-i) , how does that count number of triplets (l , k , r) minus 'k' which was proposed in the first 5 paras ?
Why are we adding this (k-x) * (y-i) ?
You need to understand that for a position i, k has only one. max{a[l],...,a[k]}<a[i],where (k-x) is the number of feasible l and (y-i) is the number of feasible r.
I think I understood that part. basically, all the subarrays which are not including x and y, and which are including k and i (both) .
but how does that help in counting answer ?
The contribution of the subarray a [l, r] to the answer is (r-l)-num, which means we can find num subscripts j, so that max{a[l],...,a[j]}<min{a[j+1],...,a[r]}. The method provided by the problem solution is to calculate the value of num by enumerating a[i]=min{a[j+1],...,a[r]}.
Actually, it is substracted from the answer. For a subarray
a[l..r], the beauty is ther - l - count(triplet(l, k, r)).understood, from total subarray lengths, we are subtracting the triplets which create partitions in subarrays. thanks. got it.
can you explain in problem B(div2) to have the maximum K why we need to do gcd of all the differences we got i mean from where you got the intuition to do gcd??
Hello, here is a video tutorial/editorial with solutions to these problems: D2B, D2C/D1A, D2D1/D1B1, D2D2/D1B2, D2E/D1C:
https://youtube.com/watch?v=VwY7QzStMk4
The compiler optimized away your $$$\mathcal O(n^2)$$$ loop, since
jis not being used.lol sorry, yeah!!!
I think there is a typo in D2B solution: Complexity should be: O(n.log n).
The correct complexity is $$$\mathcal O(n + \log n)$$$ — see discussion here and here.
Technically it should be $$$\mathcal{O}(n + \log m)$$$ where $$$m$$$ is the maximum value in the input.
But the input is always a permutation, meaning that $$$m = n$$$ always holds and the complexity is $$$O(n + \log n)$$$.
Good point! You're right. I had already forgotten about that.
Though it does mean the complexity becomes just $$$\mathcal{O}(n)$$$ because $$$n$$$ dominates $$$\log n$$$ when $$$n$$$ goes to infinity.
cann you explain why we have taken gcd of all the differences we got i mean out of nowhere he said about gcd how this intuition came i mean i didn't understoos the proof
Thanks for correcting me.. I was not aware of this amortized analysis.
So.. Can I say that in our problem: O(n+log M) = O(n+log n) = O(n)
where M is the maximum element of the array?
Yes
Great editorial! Really explains the concepts really well! The hints in Div 2 D allowed me to solve the problem without even reading the tutorial, the various ways to frame the problem makes it really interesting.
Thank you!
Can anyone explain the solution of problem B? I mean is there any proof that in order to move pi to position i ,|pi-i| has to be divisible by k?(Apologies for not using subscript)
Since any swap between two elements will change their position by exactly $$$k$$$, the distance between the initial position and the final position of each element will be divisible by $$$k$$$ as well.
really nice contest
unfortunately i couldn't enter it so I entered virtual
the first graph in the 1827C solution should have l before r-l
and i think the second case statement should say t[0...2l-r] instead of t[0...2r-l]
Fixed. Thanks.
first 3 problems were very easy, but i couldn't write this round:(
I think ,There is huge difference in difficulty of d than c.
Hello, I am new here, I could not solve Div.2 D, but I have a feeling that the number of inversions in the array and the size of the array together can be mapped to the required answer using some equation. for example,
Inversion = 0, we have Answer = 0.
And for max inversion we have,
Answer = summation of (i*(n-i)) from i=1 to n-1.
And the answers for the rest of the values will stay in that range.
While I could not find the function which satisfies this, am I right in thinking this way?
lct solution for 1D 206402736
Does someone know of a solution for B1 simpler than the one for B2? (probably in O(n^2)).
Obviously we need to beat the answer of $$$\sum_{l=1}^{n} \sum_{r=l+1}^{n} r-l$$$. How do we save time? Well, sorting $$$[L1,R1]$$$ and $$$[L2,R2]$$$ instead of $$$[L1,R2]$$$ saves $$$L2-R1$$$ seconds. We can only split the sort up like this if $$$max(L1...R1)<min(L2...R2)$$$, otherwise some elements will be in the wrong position. So, for each index $$$k$$$, we need to count the number of pairs $$$(l, r)$$$ s.t. $$$max(l...k)<min(k+1...r)$$$. Essentially we are counting the number of subarrays that use index $$$k$$$ as a "boundary point": point where we can save time by dividing the big sort into two smaller sorts. A "boundary range" that we all don't need to sort we can think of as many "boundary points." The final answer is naive answer time — # of boundary points.
Time complexity: $$$O(n^2)$$$ or $$$O(n^2 lgn)$$$
thanks! I'll implement it.
F without any data structures: 207285734. Took me just 10 hours to solve this problem.
I find that you use divide and conquer. Can you explain your solution?
I used divide and conquer not to solve the problem, but to find some helper array. I wanted to know for every index $$$i$$$ what is the number of segments of the initial array with their right bound at $$$i$$$ that are copiums. I actually have no idea what is the easiest way to solve such a subproblem, and the easiest way I found was d&c.
Ladies and gentlemen, E solution that's $$$O(N+M\log N)$$$ instead of $$$O(N\log N)$$$. As you can see, I'm focusing on the important things. 207457936
At this point, I'm pretty sure $$$O(N+M)$$$ can't be done, but you're welcome to prove me wrong. At least it's $$$O(N+M)$$$ in practice, with the only bad cases being handcrafted to make as many paths as possible get used in multiple depths of recursion. A bit over 1/2 of real runtime is taken up by reading the input and running an initial DFS, so there's not much left to optimise that'd be at least a little bit specific to this problem.
Problem D2 can be solved using simple sorting instead of a sparse table. But the time complexity remains O(nlogn). Here is the solution https://mirror.codeforces.com/contest/1828/submission/211818091
int main() { ios_base::sync_with_stdio(false); cin.tie(NULL);
/////////////////////////////////////////////////
ll t; cin>>t; while(t--) { ll n; cin>>n;
vector<ll> a(n); vector<ll> b(n); for(int i = 0; i < n; i++) cin>>a[i]; for(int i = 0; i < n; i++) cin>>b[i]; unordered_map<ll, ll> m; sort(a.begin(), a.end()); sort(b.begin(), b.end()); int i = n-1, j = n-1; while(j >= 0) { while(i > 0 and a[i] > b[j]) { i--; } if(a[i] <= b[j]) i++; m[b[j]] = n-i; j--; } // for(auto it : m) { // cout<<it.first<<" "<<it.second<<endl; // } ll modulo = pow(10, 9) + 7; ll res = m.find(b[n-1])->second; ll dif = 1; for(int i = n-2; i >= 0; i--) { ll num = m.find(b[i])->second - dif; // cout<<"num "<<num<< endl; if(num < 0) num = 0; res =(res * num) %modulo; dif++; } cout<<res%modulo<<endl;} }
It is giving STATUS_ACCESS_VIOLATION .... I have no idea why , please anyone help me
Div1-C can also be solved in $$$O(n\log^2{n})$$$ using dsu.
This solution doesn't require the lemma of the editorial, and is based on the fact that if the prefix of any even palindrome is an even palindrome, then the suffix can always be divided into disjoint even palindromes.
(note to self: write complete explanation later)
Implementation: link
Cam somebody explain the intuition behind 1828B? I am not able to understand how calculating GCD is the answer. Part about how to find the right pos is obvious but I am not able to understand GCD part.
Since any swap between two elements will change their position by exactly $$$k$$$, the distance between the initial position and the final position of each element will be divisible by $$$k$$$ as well.
So, a valid value of $$$k$$$ must be a divisor of the difference between all the initial position ($$$i$$$) and the final position ($$$p_i$$$) of each element, which is $$$|i - p_i|$$$. The largest value of $$$k$$$ is thus the greatest common divisor (GCD!) of $$$|1 - p_1|, |2 - p_2|, \dots, |n - p_n|$$$.
Hi in the 1827A — Counting Orders
why the output for following given test case is 1?
1 2 1
here a=[2] and b=[1] so aren't they already ordered? so it should be zero right?
Sorry for the confusion caused, the original array $$$a$$$ does count towards the answer
Sorry I didn't get. Does that mean the answer should be zero for this test case? input is
1
2
1
a=[2], b=[1]
Answer is $$$1$$$: $$$a = [2]$$$
Got it! Thanks for the reply