#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize("Ofast","inline","-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#define int long long
const int MOD=998244353;
void Delta() {
int a,b,c,d;
cin >> a >> b >> c >> d;
cout << (a+b>c+d?"YES":"NO") << endl;
}
signed main() {
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin >> T;
while(T--) Delta();
}
The probability of Alice's winning is strictly higher than Bob's iff $$$l_1+r_1>l_2+r_2$$$.
Lemma1:The distribution of scores for two dice rolls is symmetrical, with the axis of symmetry being $$$l+r$$$.
For example,for $$$[2,4]$$$,the distribution of scores is $$$4,5,5,6,6,6,7,7,8$$$.
Lemma2:For two intervals with the same axis of symmetry(i.e. $$$l1+r1=l2+r2$$$),Alice's probability of losing is always equal to the probability of winning.
Proof:For any $$$x∈[l1,r1]$$$,assume in $$$[l2,r2]$$$ there're $$$a$$$ numbers smaller than $$$x$$$ and $$$b$$$ numbers greater than $$$x$$$,we can infer — for $$$(l1+r1-x)$$$,there're $$$b$$$ numbers smaller than $$$(l1+r1-x)$$$ and a numbers greater than $$$(l1+r1-x)$$$.
The proof uses the symmetry of Lemma1.
Similar to Lemma2,we can infer if $$$l1+r1>l2+r2$$$ Alice's probability of winning is strictly greater than Bob's and so on.
Submitting this code directly will get ILE, please delete cerr and submit.
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize("Ofast","inline","-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
namespace Fact {
vector<char> isPrime;
vector<int> Prime,OneFac;
void GetPrime(int n){for(int i=0;i<n;++i)isPrime[i]=1;isPrime[1]=1;for(int i=2;i<=n;i++){if(isPrime[i])Prime.push_back(i);for(int j:Prime){if(i*j>n) break;isPrime[i*j]=0;OneFac[i*j]=j;if(i%j==0)break;}}}
void Fac_dfs(int x,int y,vector<int>& ans,vector<pair<int,int>>& FacList){if(x==(long long)(FacList.size())){ans.push_back(y);return;}int k=1;for(int i=0;i<=FacList[x].second;++i){Fac_dfs(x+1,y*k,ans,FacList);k*=FacList[x].first;}}
vector<pair<int,int>>GetPrimeFac(int a){vector<pair<int,int>>answer;if(isPrime[a])return(vector<pair<int,int>>{pair<int,int>{a,1}});answer.push_back({OneFac[a],1});a/=OneFac[a];while(!isPrime[a]){if(OneFac[a]==answer.back().first)answer.back().second++;else answer.push_back({OneFac[a],1});a/=OneFac[a];}if(a==answer.back().first)answer.back().second++;else answer.push_back({a,1});return(answer);}
vector<int>GetFacList(int a){vector<int> ans;vector<pair<int,int>>FacList=GetPrimeFac(a);Fac_dfs(0,1,ans,FacList);return(ans);}
void init(int n){isPrime.resize(n+2);OneFac.resize(n+2);GetPrime(n);}
void init(){init(10000005);}
};
#define int long long
const int MOD=998244353;
void Delta() {
int a,b;
cin >> a >> b;
if(Fact::isPrime[a]||(a/Fact::OneFac[a]<b)) cout << "NO" << endl;
// in code "OneFac" is The smallest non-1 factor.
else {
cout << "YES" << endl;
for(int i=1;i<b;++i) cerr << Fact::OneFac[a] << ' ';
cerr << a-(b-1)*Fact::OneFac[a] << endl;
}
}
signed main() {
Fact::init(100001);
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin >> T;
while(T--) Delta();
}
Let's say we finally get the gcd $$$x$$$, so all $$$a_i$$$ are multiples of $$$x$$$.
We want all $$$a_i$$$to be positive, so every $$$a_i$$$ is at least $$$x$$$, and all sums are at least $$$kx$$$ and sum is divisible by $$$x$$$ (You have some $$$a_i$$$ that is divisible by $$$x$$$, add it up, and it's still divisible by $$$x$$$).
Since we already know sum (is $$$n$$$), $$$x$$$ can only be a factor of $$$n$$$, Since $$$x>1$$$, just to take the smallest non-1 factor of $$$n$$$ and check. If $$$kx$$$ is less than $$$n$$$, then just put all the rest on $$$a_k$$$, which still guarantees that gcd=x.
(The constructional output is given in cerr of code for help understand)
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize("Ofast","inline","-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#define int long long
const int MOD=998244353;
int n,m,sum;
map<int,int> a,b,c;
vector<pair<int,int>> Q;
void dfs(int idx,int A,int B,int C) {
if(idx==(int)Q.size()) {
sum+=a[A]*b[B]*c[C];
return;
}
for(int i=0,t1=1;i<=Q[idx].second;++i,t1*=Q[idx].first)
for(int j=i,t2=1;j<=Q[idx].second;++j,t2*=Q[idx].first)
for(int k=j,t3=1;k<=Q[idx].second;++k,t3*=Q[idx].first)
if(k==Q[idx].second)
dfs(idx+1,A*t1,B*t2,C*t3);
}
void Delta() {
cin >> n >> m;
for(auto i:{&a,&b,&c})
for(int j=1,x;j<=n;++j) {
cin >> x;
++(*i)[x];
}
for(int i=2;i*i<=m;++i)
while(m%i==0) {
if(Q.empty()||Q.end()[-1].first!=i) Q.push_back({i,1});
else Q.end()[-1].second++;
m/=i;
}
if(m!=1)
if(Q.empty()||Q.end()[-1].first!=m) Q.push_back({m,1});
else Q.end()[-1].second++;
else;
dfs(0,1,1,1);
cout << sum << endl;
}
signed main() {
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
Delta();
}
If a number is less than $$$10^9$$$, it has a maximum possible factor of $$$1344$$$, enumerate two factors of $$$m$$$, then divide the third factor, and then use map to do count to pass.
In this table you can find all the values of $$$\text{d}(n)$$$ and $$$ω(n)$$$ for your future use :)
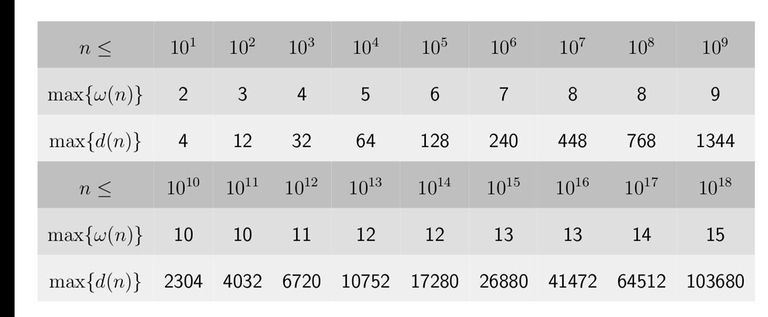
upd:
$$$\text{d}(n)$$$ = the number of different factors, and $$$ω(n)$$$ = the number of different prime factors
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize("Ofast","inline","-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#define int long long
const int MOD=998244353;
int a[500001];
void Delta() {
int n,x; cin >> n >> x;
if(x<n-1||x>(n/2)*(n-n/2)) {
cout << -1 << endl;
return;
}
for(int i=2;i<=n/2+1;++i) cout << i-1 << ' ' << i << endl;
x-=n-1;
for(int i=n/2+2;i<=n;++i) {
cout << min(x,n/2-1)+1 << ' ' << i << endl;
x-=min(x,n/2-1);
}
}
signed main() {
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin >> T;
while(T--) Delta();
}
The key to solving the problem is — consider constructing a tree with the highest score first.
It's obvious all leaf have the same LCA (othwise,link leaves with smaller depths next to leaves with larger depths, and the score will not decrease) .Note $$$x$$$ as the number of leaf nodes,then the score is $$$x(n-x)$$$,when $$$x=\lfloor\frac{n}{2}\rfloor$$$,it reaches the maximum.
From the tree with the highest score, we can easily construct a tree with any score (by moving each leaf node up).
The intended solution is $$$\Theta(n)$$$. However,if your implementation of $$$O(n\log n)$$$ solution is good, it is also possible to pass :)
There're several $$$O(n)$$$ solution.
For convenience,note $$$A={a_1,a_2,...,a_n}$$$ and $$$B={a_{n+1},a_{n+2},...,a_{2n}}$$$($$$A,B$$$ are circular).
Calculate $$$preA$$$ and $$$sufB$$$:
$$$\text{preA}_i:\max(a_j+...+a{i-1}+a_{i})$$$;
$$$\text{sufB}_i:\max(b_i+b_{i+1}+...+b_{j})$$$;
This can be solved using monotonic stacks in $$$\Theta(n)$$$.
Then reverse $$$A,B$$$ and do it again.
The answer is the maximum of the following values:
$$$\max(\text{preA}_i);$$$
$$$\max(\text{sufB}_i);$$$
$$$\max(\text{preA}_i+\text{sufB}_{i+1}).$$$
#include <map>
#include <set>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <cstdio>
#include <cstdlib>
#include <vector>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
typedef double db;
typedef long long ll;
typedef unsigned long long ull;
const int N=3000010;
const int LOGN=28;
const ll TMD=0;
const ll INF=2147483647;
int T,n;
ll ans;
int a[N],b[N],Q[N];
ll Sa[N],Sb[N],prea[N],sufb[N];
void solve()
{
for(int i=1;i<=n;i++) a[i+n]=a[i],b[i+n]=b[i];
for(int i=1;i<=n*2;i++) Sa[i]=Sa[i-1]+a[i],Sb[i]=Sb[i-1]+b[i];
int head=1,tail=0;
for(int i=1;i<=n*2;i++)
{
if(i>n)
{
while(i-Q[head]>n) head++;
prea[i-n]=Sa[i]-Sa[Q[head]];
}
while(head<=tail&&Sa[Q[tail]]>Sa[i]) tail--;
Q[++tail]=i;
}
head=1;tail=0;
for(int i=n*2;i;i--)
{
while(head<=tail&&Sb[Q[tail]]<Sb[i]) tail--;
Q[++tail]=i;
if(i<=n)
{
while(Q[head]-i+1>n) head++;
sufb[i]=Sb[Q[head]]-Sb[i-1];
}
}
for(int i=1;i<=n;i++) ans=max(ans,prea[i]);
for(int i=1;i<=n;i++) ans=max(ans,sufb[i]);
for(int i=1;i<n;i++) ans=max(ans,prea[i]+sufb[i+1]);
ans=max(ans,prea[n]+sufb[1]);
}
int main()
{
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&b[i]);
ans=-INF;
solve();
for(int i=1,j=n;i<j;i++,j--) swap(a[i],a[j]),swap(b[i],b[j]);
solve();
cout<<ans<<'\n';
}
return 0;
}
We can see how to merge the largest subsegment of two intervals and by GSS1 in $$$\Theta(1)$$$ time, so using a seg tree and just enumerates all possible k and computs it in $$$O(\log n)$$$ time. This is $$$O(n\log n)$$$.
As you can see, each query is a prefix or suffix of a single array, so we can use the prefix sum and the suffix sum, this is $$$\Theta(n)$$$.
I mentioned a minimum-memory solution in the announcement comment, so now explain how to do $$$\text{12,000 KB}$$$.
For this $$$\Theta(n)$$$ level's memory we can only save int32 a[].
For the prefix sum, just save the value of the previous one, and then add it up, you can do $$$\Theta(1)$$$ memory.
For suffix sum, do the normal suffix sum first, and save the suffix sum values on all $$$k·\sqrt{n}$$$ locations. Then compute each sqrt block separately, $$$\Theta(\sqrt{n})$$$ saves its suffix, computes its perfix recursively, and releases the memory after the calculation is complete.
This allows us to achieve memory complexity $$$\Theta(\text{sqrt})$$$ and time complexity $$$\Theta(n)$$$ in addition to "int32 a[]".
It's $$$\text{12,000 KB}$$$.
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize("Ofast","inline","-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
int a[3000010];
#define int long long
#define B 1000
class node{public:int sum,lm,rm,ans;}temp;
inline void merge1(node&a,node&l,node&r){a={l.sum+r.sum,max(l.lm,l.sum+r.lm),max(r.rm,r.sum+l.rm),max({l.ans,r.ans,l.rm+r.lm})};}
inline void merge2(node&a,node&l,node&r){a={l.sum+r.sum,min(l.lm,l.sum+r.lm),min(r.rm,r.sum+l.rm),min({l.ans,r.ans,l.rm+r.lm})};}
inline node i2node(int x){return {x,x,x,x};}
node sufb[1500010/B+10],sufnb[1500010/B+10],tsuff[B+10],tsufnf[B+10];
void Delta() {
int n,s=-2147483648,sum=0,flag=true,mx=-2147483648;cin >> n;
for(int i=1;i<=n*2;++i) {
cin >> a[i];sum+=(int)a[i];
flag&=a[i]<0;mx=max(mx,(int)a[i]);
}
node pre=i2node(0),pren=i2node(0),suf=i2node(0),sufn=i2node(0);
for(int i=n;i>=1;--i) {
temp=i2node(a[i]);
merge1(suf,temp,suf);
temp=i2node(a[i+n]);
merge1(sufn,temp,sufn);
if(i%B==0) {
sufb[i/B]=suf;
sufnb[i/B]=sufn;
}
}
for(int i=1;i<=n;++i) {
temp=i2node(a[i]);
merge1(pre,pre,temp);
temp=i2node(a[i+n]);
merge1(pren,pren,temp);
if(i%B==0||i==1) {
tsuff[B]=sufb[i/B+1];
tsufnf[B]=sufnb[i/B+1];
for(int j=(B-1);j>=1;--j) {
temp=i2node(i-(i==1)+j>n?0:a[i-(i==1)+j]);
merge1(tsuff[j],temp,tsuff[j+1]);
temp=i2node(i-(i==1)+j+n>2*n?0:a[i-(i==1)+j+n]);
merge1(tsufnf[j],temp,tsufnf[j+1]);
}
}
merge1(temp,pren,tsuff[i%B+1]);
merge1(temp,temp,pre);
merge1(temp,temp,tsufnf[i%B+1]);
s=max(s,temp.ans);
}
pre=pren=suf=sufn=i2node(0);
for(int i=n;i>=1;--i) {
temp=i2node(a[i]);
merge2(suf,temp,suf);
temp=i2node(a[i+n]);
merge2(sufn,temp,sufn);
if(i%B==0) {
sufb[i/B]=suf;
sufnb[i/B]=sufn;
}
}
for(int i=1;i<=n;++i) {
temp=i2node(a[i]);
merge2(pre,pre,temp);
temp=i2node(a[i+n]);
merge2(pren,pren,temp);
if(i%B==0||i==1) {
tsuff[B]=sufb[i/B+1];
tsufnf[B]=sufnb[i/B+1];
for(int j=(B-1);j>=1;--j) {
temp=i2node(i-(i==1)+j>n?0:a[i-(i==1)+j]);
merge2(tsuff[j],temp,tsuff[j+1]);
temp=i2node(i-(i==1)+j+n>2*n?0:a[i-(i==1)+j+n]);
merge2(tsufnf[j],temp,tsufnf[j+1]);
}
}
merge2(temp,pren,tsuff[i%B+1]);
merge2(temp,temp,pre);
merge2(temp,temp,tsufnf[i%B+1]);
s=max(s,sum-temp.ans);
}
cout << (flag?mx:s) << '\n';
}
signed main() {
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin >> T;
while(T--) Delta();
}
#include<bits/stdc++.h>
using namespace std;
#pragma GCC optimize("Ofast","inline","-ffast-math")
#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#define int long long
const int MOD=998244353;
int a[200001],b[200001],vis[200001];
vector<int> Q[200001];
void dfs(int x) {
if(vis[x]) return;
vis[x]=true;
for(int i:Q[x]) dfs(i);
}
void Delta() {
int cnt=0,blk=0,n; // count,block number
cin >> n;
for(int i=1;i<=n;++i) {
cin >> a[i];
b[i]=a[i];
Q[i].clear();
vis[i]=0;
}
sort(b+1,b+1+n);
for(int i=1;i<=n;++i)
if(a[i]!=b[i]) {
Q[a[i]].push_back(b[i]);
Q[b[i]].push_back(a[i]);
} else cnt++;
for(int i=1;i<=n;++i)
if(!vis[a[i]]&&a[i]!=b[i]) {
blk++;
dfs(a[i]);
}
if(n==2) {
if(cnt==2) cout << 0 << endl;
else cout << -1 << endl;
return;
}
if(cnt!=0) cout << blk+(n-cnt) << endl;
else if(blk==1) cout << n+2 << endl;
else cout << n+blk << endl;
}
signed main() {
ios_base::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin >> T;
while(T--) Delta();
}
Compare the original array (say $$$a$$$) to the sorted one (say $$$b$$$). Since we can move only one token at once, in one move we can place at max one token to its correct place. So let's try to minimise the number of moves that don't do this.
To make optimal moves, model a directed multi-edged graph. Start with only vertices ($$$1$$$ to $$$n$$$), no edges, and add a directed edge from $$$a[i]$$$ to $$$b[i]$$$ when $$$a[i]!=b[i]$$$, for each $$$i$$$ (meaning that $$$b[i]$$$ should be placed in place of $$$a[i]$$$).
We can follow an optimal scheme like this: For now let us assume there is at least one position where correct token is placed (let it be $$$p$$$). Choose an incorrectly placed token, place it on top of $$$p$$$. This creates a gap. Place the correct token for this place. This moves the gap somewhere else. Again choose a corect token for the gap and so on. In the end, place the token stacked on top of $$$p$$$ into the gap, close the gap, and all the tokens we touched are placed correctly.
In the graph, placing a token from $$$b[i]$$$ to gap at $$$a[i]$$$ would mean moving from $$$a[i]$$$ to $$$b[i]$$$ in the graph along an edge and removing the edge. Thus the problem reduces to removing all edges of the graph in minimum number of moves.
The graph is split into disjoint connected componnts. We can thus independently resolve each component optimally for minimum number of moves.
Next, we prove that a connected component is always an euler circuit.
Claim $$$1$$$: The component would have a cycle. If it doesn't, then following some path $$$a \rightarrow b \rightarrow ...$$$, we will reach a dead end, which means that the last element has no place to go, which is not true since it belongs to the array and must have a correct position to be placed at. By induction, we can keep removing cycles (by moving along them and removing edges), and so the component is basically a set of directed cycles intersecting at vertices.
Claim $$$2$$$: It will hence form an euler circuit. Let us go along a cycle. It starts at $$$v$$$, ends at $$$v$$$. Now if there is a cyce intersecting at some vertex $$$v'$$$ in the cycle, on reaching $$$v'$$$ resolve that cycle, return at $$$v'$$$, continue on the older cycle. By this inductive argument, we can cover all edges exactly once and return to $$$v$$$, making an euler circuit.
To find the precise number of moves to resolve a component involving $$$s$$$ tokens, we need to create a gap in $$$1$$$ move, place $$$s-1$$$ tokens correctly, and place the last token we moved initially. Total $$$s+1$$$ moves. To create a gap, we need to place a token from our position to some position not in the component.
Now, proper casework:
Let the number of tokens not placed correctly be $$$co$$$. Let the number of disjoint connected components be $$$x$$$.
If $$$co<n$$$: There is always a correctly placed position to stack our token on and create a gap. So, each component of size s will be resolved in $$$s+1$$$. So total $$$co+x$$$ moves.
If $$$x>1$$$: Since there are $$$>1$$$ components, we can use a position from the other component to create gap for one component. Again $$$co+x$$$.
$$$co==n$$$ and $$$x==1$$$: It may be a single cycle, or $$$>1$$$ joint cycles. If there are $$$>1$$$ joint cycles, resolve one of the cycles, then it reduces to the cases above. Totals to $$$n+2$$$ moves. For exactly one cycle, graph is $$$1 \rightarrow 2 \rightarrow ...n \rightarrow 1$$$. So stack $$$1$$$ on $$$2$$$, resolve rest $$$n-2$$$, total $$$n-1$$$. Then resolve $$$1$$$ and $$$2$$$ which takes $$$3$$$ moves. So total again is $$$n+2$$$. Since $$$n+1$$$ is not possible in this case, and we construct a solution in $$$n+2$$$, it is optimal.
Final solution:
$$$(co < n)$$$ or $$$(x>1)$$$ : $$$co+x$$$
$$$(co==n)$$$ and $$$(x==1)$$$ : $$$n+2$$$










[Deleted]
You can copy the code from the Editorial and submit it. After you get AC, you will be able to view the test data.
can u explain how to get the d(n),w(n) for largenumbers(like 10^18) in efficient way ? sorry if i am pointless here.
for max(d(n)):
http://wwwhomes.uni-bielefeld.de/achim/highly.html
for max(w(n)):
Just go from small to big and greedy and pick 2,3,5,7,11,13,17,(all prime).... and multiply
There's no good algo here for specific d(n) and w(n), except to do the decomposition with PollardRho or something like that.
In this: You can copy the code from the Editorial and submit it. After you get AC, you will be able to view the test data.
Then why I'm not able to view the test data of problems A, B? I got AC on both of them.
Sry,it seems impossible to show test data in any gym contests
what is w(n) and d(n) in editorial of C?
In this case n is odd and not prime. According to the solution, we first need to find the smallest divisor of N, let it be x. x = 1 and N / x = 15 > K = 4. Suppose the solution says x > 1. Then x = 3 and again N / x = 5 > K = 4 and answer is NO but actual answer is YES.
Solution didn't need to mention case k = 1.
EDIT: fixed
Answer is YES since 15 can be broken into 3, 3, 3, 6 with gcd = 3 > 1
I also said answer is YES but solution's(editorial's) answer is NO. Please read the comment carefully before replying it.
EDIT: fixed
Yes, you're correct. It should N/x >= k in editorial.
Sorry for b bad editorial, rewrote a new version.
wasn't A supposed to be the easiest problem? the math was hard. couldn't solve it and get disapointed.
Solution for B better than editorial.. It's sufficient to check the condtion for spf only And all test case can be answer in O(1) . Link for code: https://mirror.codeforces.com/gym/104455/submission/211966383
anyone explain D editorial is not clear
You can refer to this code : https://mirror.codeforces.com/gym/104455/submission/211985521 First try to find the max possible ans.. which u can think like sum is fixed u have find max product ( which comes at middle) i.e. the max ans possible is ((n/2)*((n+1)/2)) and this will be possible when u will move (n-1)/2 steps downward (say node n1) and considering that node as ancestor connect all left node to its direct child.. And the min ans you can get here is when all node will be connected serial-wise or connected directly to node 1 which will be n-1.. So, if given x lie between min and max value means we can find a tree for x; To find a tree for a particular x we will find the difference between the max possible ans and the given x, then u will be known how much ans you have to decrease.. Accordingly we will connect those node to node 1 directly to reduce the max value. For further u can see the given code..
can some give example of A for clear understanding, how l1+r1>l2+r2 is answer??
Would you please investigate submission 212018133 (I submitted using one of my alts)?
It is copied directly from the editorial but also gets TLE on test6. It seems that we could only pass this problem using C++17, not even C++20, let along Python.
[user:wuhudsm][user:EndlessDreams]
For problem E:
It is also ok to directly swap $$$a$$$ and $$$b$$$ by symmetry, i.e., replace the line
for(int i=1,j=n;i<j;i++,j--) swap(a[i],a[j]),swap(b[i],b[j]);with
for(int i = 1; i <= n; ++i) swap(a[i], b[i]);But be careful,
swap(a, b)would lead to TLE, because it will calltemplate< class T2, std::size_t N > void swap( T2 (&a)[N], T2 (&b)[N] );(until C++11)template< class T2, std::size_t N > void swap( T2 (&a)[N], T2 (&b)[N] ) noexcept;(Since C++11 Until C++20)template< class T2, std::size_t N > constexpr void swap( T2 (&a)[N], T2 (&b)[N] ) noexcept(Since C++20)See https://en.cppreference.com/w/cpp/algorithm/swap for detail. So swap(a, b) will run through the whole array and causes TLE.
Code:
My TLE (on test 6) solution during the competition (Using DDP+Segtree) is attached below. It might work if the time limit is looser:
Why are the problems deleted? I saw they'd faded away from submissions and also upon clicking on any problem via editorial, it says contest has not started yet.
why the contest is restarting?