We hope you liked the problems.
Task A was invented and prepared by induk_v_tsiane.
Task B was invented by induk_v_tsiane, and prepared by i_love_penguins.
Task C was invented and prepared by induk_v_tsiane.
Task D was invented by i_love_penguins and efimovpaul, and prepared by i_love_penguins.
Task E was invented by induk_v_tsiane and kristevalex, and prepared by induk_v_tsiane.
Task F was invented by induk_v_tsiane and Artyom123, and prepared by induk_v_tsiane.
What does it mean that $$$A$$$ divides $$$B$$$?
First, if all numbers are equal, then there is no answer (since $$$a$$$ is divisible by $$$a$$$, if both arrays are non-empty, then $$$c_1$$$ is a divisor of $$$b_1$$$).
Second, if $$$a$$$ is divisible by $$$b$$$ and they are both natural numbers, then the following equality holds: $$$b \le a$$$ (by definition, if $$$a$$$ is divisible by $$$b$$$, then $$$a$$$ can be represented as $$$k \dot b$$$, where $$$k$$$ is a natural number).
Now we can place all instances of the smallest number into $$$b$$$, and all other numbers into $$$c$$$. It can be seen that such a construction always gives a valid answer.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
void solve() {
int n = 0; cin >> n;
vector<int> inp; inp.assign(n, 0);
for (auto& x : inp) cin >> x;
sort(inp.begin(), inp.end());
if (inp.back() == inp[0]) {
cout << "-1\n";
return;
}
else {
int it = 0;
while (inp[it] == inp[0]) it++;
cout << it << " " << n - it << "\n";
for (int j = 0; j < it; ++j) cout << inp[j] << " ";
for (int j = it; j < n; ++j) cout << inp[j] << " ";
}
}
int main() {
int t = 0; cin >> t;
while (t--) solve();
return 0;
}
1859B - Olya and Game with Arrays
Do all numbers in a single array really matter?
If only the first minimum and the second minimum matter, what is the only way to increase a single array's beauty?
What can we say about the array which will have the smallest number in the end?
To increase the answer for each array separately, it is necessary to move the minimum to another array. Then, notice that it is optimal to move all the minimums to one array. Let's figure out which array. After moving the minimum from an array, the second minimum in the original array becomes the new minimum. Then, it is easy to notice that it is optimal to move all the minimums to the array with the smallest second minimum. After all the movements, we will have one array where the minimum element is the smallest number among all the arrays, and $$$n-1$$$ arrays where the minimum element is the second minimum in the original array.
Therefore, the answer to the problem will be $$$M + K - S$$$, where $$$M$$$ is the minimum element among all the arrays, $$$K$$$ is the sum of all the second minimums, and $$$S$$$ is the smallest second minimum.
#include <iostream>
#include <vector>
#include <algorithm>
#include <numeric>
using namespace std;
#define all(v) v.begin(), v.end()
typedef long long ll;
const int INF = 1e9 + 7;
void solve() {
int n;
cin >> n;
int minn = INF;
vector<int> min2;
for (int i = 0 ; i < n ; i++) {
int m;
cin >> m;
vector<int> v(m);
for (auto &el : v) cin >> el;
int minel = *min_element(all(v));
minn = min(minn, minel);
v.erase(find(all(v), minel));
min2.push_back(*min_element(all(v)));
}
cout << minn + (ll) accumulate(all(min2), 0ll) - *min_element(all(min2)) << "\n";
}
signed main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
#ifdef LOCAL
freopen("a.in", "r", stdin);
#endif
int t = 1;
cin >> t;
while (t--)
solve();
return 0;
}
1859C - Another Permutation Problem
What if we fix the maximum element in the resulting array?
Try using greedy.
Optimize the log factor away by noticing a certain fact.
Let's fix the maximum element in an array — let it be $$$M$$$. Now, let's iterate from $$$n$$$ to $$$1$$$. Let the current chosen number be $$$i$$$. I claim that if we maintain the remaining available numbers to multiply by, then it is optimal to take the maximum such number $$$x$$$ that $$$x * i \le M$$$.
Proof: let's say that this is not correct. Then, let's say that we pair $$$i$$$ with another number $$$x1$$$, and $$$x$$$ gets paired with some other number $$$i1$$$. Then, $$$i1 < i$$$, because it was chosen later, and $$$x1 < x$$$ (otherwise $$$i * x1 > M$$$). Now let's swap $$$x$$$ with $$$x1$$$. The sum is increased by $$$i * x - i * x1 - i1 * x + i1 * x1 = (i - i1)(x - x1) > 0$$$, and all of the numbers are less or equal to $$$M$$$.
Now the task can be solved in $$$O(N^3logN)$$$ by simply iterating on the maximum from $$$N^2$$$ to $$$1$$$, while maintaining the remaining numbers with a set. In order to squeeze it in the TL, you can only consider such maximums that they can be represented as $$$i * j, 1 \le i, j \le n$$$.
In order to optimize it to $$$O(N^3)$$$, let's notice that for each number $$$x$$$, it can be paired with any number from $$$1$$$ to $$$\frac{M} {x}$$$. Now just maintain a stack of all available elements at the current moment, add all numbers that possible, and pop the maximum number for all $$$i$$$ from $$$1$$$ to $$$N$$$.
#include <iostream>
#include <algorithm>
#include <set>
#include <stack>
#include <vector>
using namespace std;
void solve() {
int N = 0; cin >> N;
int ans = 0;
vector<int> pr;
pr.assign(N * N, -1);
for (int i = 1; i <= N; ++i) {
for (int j = 1; j <= N; ++j) {
pr[i * j - 1] = 1;
}
}
for (int mx = N * N; mx >= 1; --mx) {
if (pr[mx - 1] == -1) continue;
vector<vector<int>> a;
int curans = -mx;
bool br = false;
a.assign(N, vector<int>());
for (int j = N; j >= 1; --j) {
int num = min(mx / j, N);
if (num < 1) {
br = true;
break;
}
a[num - 1].push_back(j);
}
if (br) break;
stack<int> s;
for (int i = 0; i < N; ++i) {
s.push(i + 1);
bool brk = false;
for (auto x : a[i]) {
if (s.empty()) {
brk = true; break;
}
curans += s.top() * x;
s.pop();
}
if (brk) break;
}
ans = max(ans, curans);
}
cout << ans << "\n";
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int t = 0; cin >> t;
while (t--) solve();
return 0;
}
1859D - Andrey and Escape from Capygrad
What if we use greedy a bit?
Where it is always beneficial to teleport?
Use scanline
Statement: It is always beneficial to teleport to point $$$b_i$$$.
Proof: Let's assume that we were able to teleport from point $$$X$$$ to the right of $$$b_i$$$, but not from $$$b_i$$$. Then we used some segment $$$A$$$ that covers point $$$X$$$, but does not cover point $$$b$$$, and ends to the right of $$$b$$$. This is a contradiction.
Let $$$ans_i$$$ be the maximum coordinate we can reach while being on segment $$$i$$$, and let $$$p_j$$$ be the answer to the $$$j$$$-th query. Then we notice that the answer to query $$$p_j = \max(x_j, \max_{i = 1}^n {ans_i \vert l_i \le x_j \le r_i})$$$.
We will use the scanline method from the end. Events: $$$l_i$$$, $$$b_i$$$, $$$r_i$$$, $$$x_j$$$.
We notice that events of type $$$r_i$$$ are not important to us when scanning from the end (according to statement number 1). It is important for us that we process events of type $$$b_i$$$ first, then events of type $$$x_j$$$, and then events of type $$$l_i$$$ (closing the segment in the scanline).
We will go through the events of the scanline, processing them in the order of $$$b_i$$$, then events of type $$$x_j$$$, and then events of type $$$l_i$$$.
We assume that there is a data structure that allows us to add elements, remove elements, and quickly output the maximum.
For each event of type $$$b_i$$$, update the value of $$$ans_i$$$ — take the maximum value of $$$ans$$$ of all open segments from the structure.
For each event of type $$$x_j$$$, update the value of $$$p_j$$$ — take the maximum value of $$$ans$$$ of all open segments from the structure, as well as $$$x_j$$$.
For each event of type $$$l_i$$$, remove $$$ans_i$$$ from the structure.
We notice that to solve this problem, we can use the std::multiset} container, which automatically sorts elements in ascending order. We can store in $$$multiset$$$ $$$ans_i$$$ of all open segments. And then, when processing events, extract the maximum from $$$multiset$$$, all operations are performed in $$$O(\log n)$$$. This allows us to solve the problem in $$$O((n + q) \log n)$$$ time and $$$O(n)$$$ memory.
#include <iostream>
#include <vector>
#include <set>
#include <iomanip>
#include <cmath>
#include <algorithm>
#include <map>
#include <stack>
#include <cassert>
#include <unordered_map>
#include <bitset>
#include <random>
#include <unordered_set>
#include <chrono>
using namespace std;
#define all(a) a.begin(), a.end()
void solve() {
int n;
cin >> n;
vector<int> ans(n);
vector<tuple<int, int, int>> events;
for (int i = 0 ; i < n ; i++) {
int l, r, a, b;
cin >> l >> r >> a >> b;
ans[i] = b;
events.emplace_back(b, 1, i);
events.emplace_back(l, -1, i);
}
int q;
cin >> q;
vector<int> queries(q);
for (int i = 0 ; i < q ; i++) {
int x;
cin >> x;
queries[i] = x;
events.emplace_back(x, 0, i);
}
sort(all(events));
reverse(all(events));
multiset<int> s;
for (auto [x, type, ind] : events) {
if (type == 1) {
if (!s.empty()) {
ans[ind] = *s.rbegin();
}
s.insert(ans[ind]);
} else if (type == 0) {
if (!s.empty()) {
queries[ind] = max(queries[ind], *s.rbegin());
}
} else {
s.extract(ans[ind]);
}
}
for (auto el : queries)
cout << el << " ";
cout << "\n";
}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
solve();
return 0;
}
Maybe we can relax some conditions?
Do we really need to always correctly calculate all sums?
Optimize the obvious dp.
Let's call the value of a segment $$$[l; r]$$$ $$$f(l, r) = abs(a_l - b_r) + abs(a_r - b_l)$$$.
Let's write $$$dp[n1][k1]$$$ — maximum value of segments of total length $$$k1$$$ that end before $$$n1$$$.
The obvious way to recalc is the following:
$$$dp[n1][k1] = max(dp[n1 - 1][k1], dp[n1 - l][k1 - l] + f(n1 - l + 1, n1), 1 \le l \le k1)$$$.
This works in $$$O(NK^2)$$$ and is too slow.
Now let's consider the following: instead of getting the absolute value of segment $$$[l; r]$$$, we consider the maximum of the following four combinations: $$$b_l - a_r + b_r - a_l$$$, $$$b_l - a_r - b_r + a_l$$$, $$$-b_l + a_r + b_r - a_l$$$, $$$-b_l + a_r - b_r + a_l$$$. We can see that this always gives us the correct answer to the absolute value, since we check all of the possibilities.
Now we can look at out dp states as a table, and notice that we recalc over the diagonal (we recalc over all states that have the same value of n1 — k1).
Now, for each "diagonal", we maintain four maximum combinations: $$$dp[n1][k1] + b_{k1} + a_{k1}, dp[n1][k1] - b_{k1} + a_{k1}, dp[n1][k1] + b_{k1} - a_{k1}, dp[n1][k1] - b_{k1} - a_{k1}$$$, and when we want to recalc state $$$dp[n2][k2]$$$, we just consider all of the four possibilities.
#include <iostream>
#include <vector>
using namespace std;
const long long INF = 1e18;
#define int long long
void solve() {
int N = 0, K = 0; cin >> N >> K;
vector<int> a;
vector<int> b;
a.assign(N, 0);
b.assign(N, 0);
for (int i = 0; i < N; ++i) {
cin >> a[i];
}
for (int i = 0; i < N; ++i) {
cin >> b[i];
}
vector<long long> mx1; // max of (b_l + a_l) + corresponding dp
vector<long long> mx2; // max of (b_l - a_l) + corresponding dp
vector<long long> mn1; // min of (b_l + a_l) + corresponding dp
vector<long long> mn2; // min of (b_l - a_l) + corresponding dp
vector<vector<long long>> dp;
mx1.assign(N + 1, -INF); mx2.assign(N + 1, -INF);
mn1.assign(N + 1, INF); mn2.assign(N + 1, INF);
dp.assign(N + 1, vector<long long>(K + 1, 0));
for (int i = 0; i <= N; ++i) {
for (int j = 0; j <= min(i, K); ++j) {
if (i != 0) dp[i][j] = dp[i - 1][j];
int diag_val = i - j;
if (i != 0) {
dp[i][j] = max(dp[i][j], b[i - 1] + a[i - 1] - mn1[diag_val]);
dp[i][j] = max(dp[i][j], -b[i - 1] - a[i - 1] + mx1[diag_val]);
dp[i][j] = max(dp[i][j], a[i - 1] - b[i - 1] - mn2[diag_val]);
dp[i][j] = max(dp[i][j], b[i - 1] - a[i - 1] + mx2[diag_val]);
}
if (i != N) {
mn1[diag_val] = min(mn1[diag_val], b[i] + a[i] - dp[i][j]);
mx1[diag_val] = max(mx1[diag_val], b[i] + a[i] + dp[i][j]);
mn2[diag_val] = min(mn2[diag_val], b[i] - a[i] - dp[i][j]);
mx2[diag_val] = max(mx2[diag_val], b[i] - a[i] + dp[i][j]);
}
}
}
cout << dp[N][K] << "\n";
}
signed main() {
int T = 1;
cin >> T;
while (T--) {
solve();
}
}
1859F - Teleportation in Byteland
How many times do we really need to take driving courses?
Can you think how would an optimal answer path look like?
Can you recalculate the distances required to get to a city from every vertex?
Root the tree arbitrarily.
First, we can notice that there is no need to take driving courses more than $$$log{maxW}$$$ times.
Now, let's iterate for the number of driving courses we take from $$$0$$$ to $$$20$$$ ($$$2^{20} > 1000000$$$). For each number we solve separately.
Let us fix the number of taken as $$$q$$$. Now the path looks like the following: we go over the simple path, then we veer off to take courses in some town, then we come back to the path and finish it. Let's call $$$d[x]$$$ the minimum distance required to get from $$$x$$$ to a town which offers driving courses and then come back to the same town. We can recalculate $$$d[x]$$$ with multi-source BFS.
Now, let's look at the vertex $$$v1$$$ on the path, from which we will start going off the path. Then, the cost of the path is $$$d[v1]$$$ + distance from $$$a$$$ to $$$v1$$$ on the original edges (with $$$c = 1$$$) + distance from $$$v1$$$ to $$$b$$$ on the modified edges(with $$$c = 2^{q}$$$).
Now let's look at some cases, let $$$LCA$$$ be the LCA of $$$a$$$ and $$$b$$$, $$$h1[x]$$$ — the sum of all original edges from the root downwards to $$$x$$$, $$$h2[x]$$$ — the sum of all modified edges from the root downwards to $$$x$$$.
If $$$v1$$$ is between $$$LCA$$$ and $$$a$$$, the cost is $$$h1[a] - h1[v1] + d1[v1] - h2[LCA] + h2[v1] + h2[b] - h2[LCA]$$$. If $$$v1$$$ is between $$$LCA$$$ and $$$a$$$, the cost is $$$h1[a] - h1[LCA] + h1[v1] - h1[LCA] + d1[v1] + h2[b] - h2[v1]$$$. Now we simply need to consider the terms which depend only on $$$v1$$$, and then we need to take the maximum value on a path. For that we can use binary lifting, and for LCA as well.
#include <iostream>
#include <iomanip>
#include <fstream>
#include <vector>
#include <numeric>
#include <algorithm>
#include <set>
#include <map>
#include <cmath>
#include <stack>
#include <deque>
#include <string>
#include <ctime>
#include <bitset>
#include <queue>
#include <cassert>
#include<unordered_set>
#include<unordered_map>
#include<string.h>
#include <random>
#include <chrono>
#include <math.h>
using namespace std;
#define pi pair<int, int>
#define ll long long
#define pll pair<ll, ll>
const ll INF = 1e18;
vector<vector<pi>> g;
vector<int> is_special;
vector<vector<int>> bin_lift;
vector<vector<pi>> new_g;
vector<int> tin;
vector<int> tout;
vector<ll> ans;
vector<pi> req;
vector<ll> h_orig;
vector<ll> h_new;
vector<ll> d;
vector<bool> used_bfs;
vector<vector<pll>> bin_lift_2;
vector<int> lc;
vector<int> top_order;
vector<pair<int, int>> pr;
int TIMER = 0;
void DFS(int v, int p) {
top_order.push_back(v);
tin[v] = TIMER++;
bin_lift[v][0] = p;
for (int i = 1; i < 17; ++i) {
if (bin_lift[v][i - 1] == -1) break;
bin_lift[v][i] = bin_lift[bin_lift[v][i - 1]][i - 1];
}
for (auto& x : g[v]) {
if (x.first == p) {
pr.push_back(x);
continue;
}
}
for (auto& x : g[v]) {
if (x.first == p) continue;
h_orig[x.first] = h_orig[v] + x.second;
DFS(x.first, v);
}
tout[v] = TIMER;
}
void BFS(int N) {
priority_queue<pll> q;
for (int i = 0; i < N; ++i) {
if (is_special[i]) {
q.push({ -0, i });
d[i] = 0;
}
}
while (!q.empty()) {
int v = q.top().second; q.pop();
if (used_bfs[v]) continue;
used_bfs[v] = true;
for (auto& x : new_g[v]) {
if (d[x.first] > d[v] + x.second) {
d[x.first] = d[v] + x.second;
q.push({ -d[x.first], x.first });
}
}
}
}
inline bool isIn(int a, int b) {
return tin[a] <= tin[b] && tout[a] >= tout[b];
}
int gLCA(int a, int b) {
if (isIn(a, b)) return a;
if (isIn(b, a)) return b;
int cB = b;
for (int i = 16; i >= 0; --i) {
if (bin_lift[cB][i] == -1) continue;
if (!isIn(bin_lift[cB][i], a)) cB = bin_lift[cB][i];
}
return bin_lift[cB][0];
}
ll g1(int a, int LCA) {
ll mn = d[a] + h_new[a] - h_orig[a];
int cK = a;
for (int i = 16; i >= 0; --i) {
if (bin_lift[cK][i] == -1) continue;
if (!isIn(LCA, bin_lift[cK][i])) continue;
mn = min(mn, bin_lift_2[cK][i].first);
cK = bin_lift[cK][i];
}
return mn;
}
ll g2(int a, int LCA) {
ll mn = d[a] + h_orig[a] - h_new[a];
int cK = a;
for (int i = 16; i >= 0; --i) {
if (bin_lift[cK][i] == -1) continue;
if (!isIn(LCA, bin_lift[cK][i])) continue;
mn = min(mn, bin_lift_2[cK][i].second);
cK = bin_lift[cK][i];
}
return mn;
}
void solve() {
top_order.clear();
pr.clear();
int N = 0, T = 0; cin >> N >> T;
g.assign(N, vector<pi>());
for (int j = 0; j < N - 1; ++j) {
int u = 0, v = 0, w = 0; cin >> u >> v >> w;
u--; v--;
g[u].push_back({ v, w }); g[v].push_back({ u, w });
}
is_special.assign(N, 0);
string s = ""; cin >> s;
for (int i = 0; i < N; ++i) is_special[i] = s[i] - '0';
tin.assign(N, 0); tout.assign(N, 0);
bin_lift.assign(N, vector<int>(17, -1));
TIMER = 0;
h_orig.assign(N, 0);
DFS(0, -1);
int Q = 0; cin >> Q;
ans.assign(Q, INF);
req.clear();
lc.clear();
for (int j = 0; j < Q; ++j) {
int u = 0, v = 0; cin >> u >> v;
u--; v--;
req.push_back({ u, v });
lc.push_back(gLCA(u, v));
}
bin_lift_2.assign(N, vector<pll>(17, pll(INF, INF)));
h_new.assign(N, 0);
for (ll level = 1; level <= 20; ++level) {
const int w = (1ll << level);
new_g.assign(N, vector<pi>());
for (int i = 0; i < N; ++i) {
for (int j = 0; j < g[i].size(); ++j) {
new_g[i].push_back({ g[i][j].first, g[i][j].second + ((g[i][j].second + w - 1) / w) });
}
}
d.assign(N, INF);
used_bfs.assign(N, false);
BFS(N);
h_new[0] = 0;
for (int n = 1; n < N; ++n) {
h_new[top_order[n]] = h_new[pr[n - 1].first] + (pr[n - 1].second + w - 1) / w;
int p = pr[n - 1].first;
int v = top_order[n];
bin_lift_2[v][0] = { d[p] + h_new[p] - h_orig[p], d[p] + h_orig[p] - h_new[p] };
for (int i = 1; i < 17; ++i) {
if (bin_lift[v][i] == -1) break;
bin_lift_2[v][i].first = min(bin_lift_2[v][i - 1].first, bin_lift_2[bin_lift[v][i - 1]][i - 1].first);
bin_lift_2[v][i].second = min(bin_lift_2[v][i - 1].second, bin_lift_2[bin_lift[v][i - 1]][i - 1].second);
}
}
for (int j = 0; j < Q; ++j) {
int a1 = req[j].first; int b1 = req[j].second;
int LCA = lc[j];
ans[j] = min(ans[j], g1(a1, LCA) + h_orig[a1] - h_new[LCA] + h_new[b1] - h_new[LCA] + level * T);
ans[j] = min(ans[j], g2(b1, LCA) + h_orig[a1] - h_orig[LCA] - h_orig[LCA] + h_new[b1] + level * T);
}
}
for (int i = 0; i < Q; ++i) {
ans[i] = min(ans[i], h_orig[req[i].first] + h_orig[req[i].second] - 2 * h_orig[lc[i]]);
cout << ans[i] << "\n";
}
}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cout << setprecision(12);
int T = 1;
cin >> T;
while (T--) {
solve();
}
return 0;
}
Some notes/challenges:
We know about the $$$O(N^2)$$$ solution in C, but we did not find a good suitable proof for it (and, using the method, we could achieve faster solutions).
You can solve $$$D$$$ without the constraint that the segments are contained, but that is harder. It is solvable in $$$(ONlogN)$$$.
Thank you all for participating! If you have any complaints/suggestions/advice for future rounds, feel free to share in the comments!










Auto comment: topic has been updated by induk_v_tsiane (previous revision, new revision, compare).
Thanks for fast editorial!
what does multiset extract do exactly? can I just use erase?
Thanks for your texts!
Problem C can be solved in O(n^2).
Yeah, I solved it in O(n^2) by кукарек, I don't know, why my solution works correctly.
maybe can be solved in O(n) too, but I don't know how to prove it
What is the O(N) idea?
I think that the recalculation of the tail from step to step could be done in O(1) — you always know where is the maximal term and the delta to sum: -sum of all values + delta for border elements
First I got all the answers for n<=13 by brute force, then subtracted this answer from the sum of the squares of all the natural numbers less than or equal to n to get a series:1 3 7 13 20 29 40 52 66 82 100 120 141
Then I subtracted each neighboring number in this series to get a second series: 2 4 6 7 9 11 12 14 16 18 20 21
Then I realized that the second series is very much like an equal-variance series, but at the no.2*3,2*5,2*7... number this difference changes to 1.
Through this strange pattern, it is possible to construct a second series (n<=250) by preprocessing, which inverts the first series to get the answer. For each example, we only need to find the sum of the squares of all the natural numbers less than or equal to n.
This is my submission:218557375
First of all, observe that the maximum cost permutation is like this:
$$$1$$$, $$$2$$$, $$$3$$$, $$$4$$$, ... , $$$p$$$, $$$n$$$, $$$n-1$$$, $$$n-2$$$, ... , $$$p+1$$$ ;
Secondly, it's provable that p=n-sqrt(2*n).
And without precalculations or other things, we can solve this problem with a kinda brute force solution in O(n).
My submission: 218725357 .
found that reversing the last k elements where k is the minimum value such that n <= k + floor(k^2/2) (which is oeis sequence) is optimal so its o(n)
don't know why it works
@eric.dai.kj yeah even i did same by obervation, but do we have any proofs for it
is it possible to calculate all the answers locally then make a script to create many if else statements to achieve a O(1) solution? just a random thought :)
but I wait the answer when n==13 for at least 7 mins,O(n!) is too terrible!:(
lol I used to do that during contest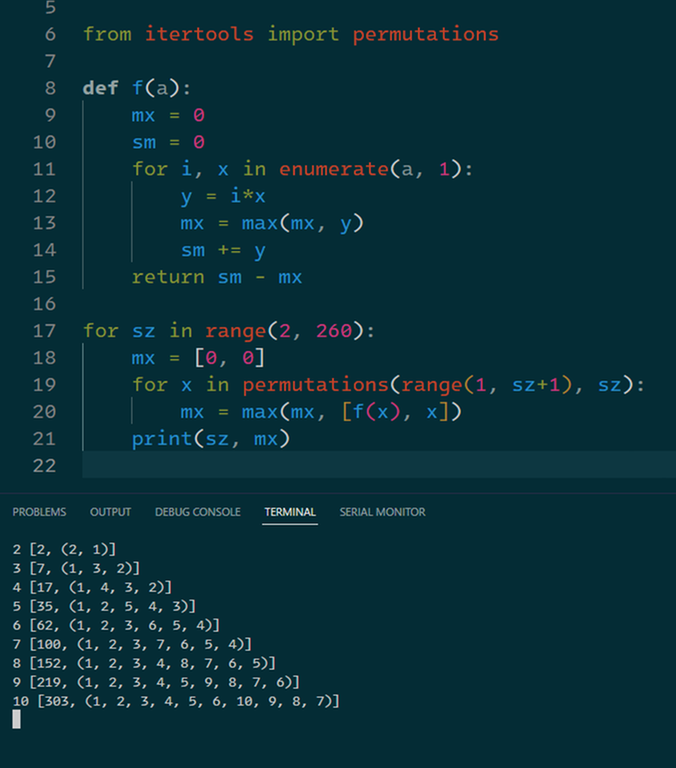
very interesting! I think we can. However calculating for all the permutations might take a lot of time. I might try this some time afterwards
218549633 bro did it lmao
You can check out my code here: https://mirror.codeforces.com/contest/1859/submission/218544590 I got a $$$O(n^4)$$$ solution but it didn't pass so I just pre-computed it :)
What is the O(N^2) idea?
For task C the optimal answer is a permutation that is the identity permutation with some suffix reversed. For example, for n = 4 you have 1 2 4 3, so you can get an O(N^2) solution.
For task C the optimal answer is a permutation that is the identity permutation with some suffix reversed. For example, for n = 4 you have 1 2 4 3, so you can get an O(N^2) solution. https://mirror.codeforces.com/contest/1859/submission/218520660
Hardest part is to prove that
there exists an easy proof strategy called "proof by ac"
"It's easy to show that..."
"... this solution is correct because it passed pretests"
That is called "verification"
I lost 30 minutes proving it
Can you please share your idea how did you prove it.
can we prove why reversing only last two elements will not work ?
Use case n=10. Does not work. $$$\square$$$
https://ru.wikipedia.org/wiki/%D0%9E%D1%87%D0%B5%D0%B2,_%D0%92%D0%B8%D1%82%D0%B0%D0%BB%D0%B8%D0%B9_%D0%93%D0%B5%D0%BE%D1%80%D0%B3%D0%B8%D0%B5%D0%B2%D0%B8%D1%87
I wrote a solution in O(N * logN) I don't know why it works, but it worked https://mirror.codeforces.com/contest/1859/submission/218544583
Damn, I've figured out how to solve problem B, but still didn't get it right. My solution have no difference between the one in the tutorial, but for some reason it failed on pretest 4.
Read about
intandlong longdatatype in c++Thanks for noticing. I didn't consider the sum being greater than 10^9. Spent last 30 minutes debugging the solution when the answer was out there.
I think, use long long, the sum can excess int
In my opinion,I always use
#define int long longso I don't need to care that I useintorlong long.i think it's not a good practice
Where is precalc in author’s solution of the problem C???
Do you really need a precalc when you have an $$$O(n^3)$$$ (or even $$$O(n^2)$$$ for most of participants) solution???
$$$\sum n\le500$$$,so $$$O(n^3)$$$ can solve it.As the result,you needn't use precalc.
Very entertaining round keep it up :)
I found C through pattern:
The solution is always in form:
I didn't prove this, does somebody have an idea why this happens? Sol is trivial O(N^2)
the stream is proving the statement uwu
This pattern was so not obvious. Almost gave up on C but then decided to loop through every permutation(next_permutation) for n=10 to see what permutation gave 303 and the pattern was there clear as hell.
same, the bruteforce was so obvious i just tried it to look for patterns (also i couldn't find the solution for 10)
initial permutation :- 1 2 3 4 ... n
k = 1 to n let say you want to change positions only in last n-k (may be not all also). so permutation will be 1 2 3 ... k — — and now we need to find for what position of other numbers (k+1 to n) will we get max ans ;
if we minimize the max value then remaining sum of values ( k+1 to n positions ) become larger and ans will be max .
let say n is at position a and n-1 is at position b . if a > b ==> abs(n*a — (n-1)*b) > abs(n*b — (n-1)*a) . As we want all numbers(k+1*val at k+1 to n*val at n) to be closer to each other we give b position n and a to n-1.
By considering all possible pairs 1 2 3 4 -- k n n+1 — k+1 gives the max ans when only we want to make changes in last n-k positions
iterate this for k = 1 to n.
Just calculate everything, put all in a list and print and print
Bruteforcing all permutations of 250 elements goes brrrr
No it's impossible as 12! is already 479001600, which is very large, we need to realize this. Then brute force for a permutation takes O(n^2) time.
Bruh why do we need the table then?
because I had been generating 10 first permutations and realize the pattern, so I pre-calculate all and submit then pray for luck, luckily it's Accepted lol
Couldn't you submit the program that calculates answers instead of the table?
you can visit my profile and look at my submission for C, it still have the precalc part
Bro had to calculate answers by hand.
yes, to be honest I don't like this way, it makes me have feeling of cheating. But I couldn't think of proper way, so I had to do like this, isn't it a wise choice :)
Yes but $$$t\leq{30}$$$
I'm telling that generate all permutation is impossible, not O(n^2) is not good enough
What if we use 100% of our brain:D
Task D: "We assume that there is a data structure that allows us to add elements, remove elements, and quickly output the maximum. ...
We notice that to solve this problem, we can use the std::multiset} container, which automatically sorts elements in ascending order."
Which other structures can be used to solve this? (preferably easy to implement)
Golang doesn't have a built-in multiset. I tried to use a priority queue, but couldn't find a version that supports removing some element by index.
In problem D, I only use vector. You could consider to see my solution submission
that's helpful, thanks!
I used stack for problem D
Can you elaborate?
So if I have an array of segments and we want to merge the intersecting segments together, I can sort the array of segments according to it’s first element, then I push each segment into a stack, either it intersects with the top of the stack, then I merge them together, or it doesn’t and then I just push it as another segment into the stack. Though I think using a vector would be better for this problem.
Yeah I used vector to merge intervals it worked quite well, Thankyou.
You can simply use vector of pairs, and then a map.
even no map is required only vector you can see my submission 218580178
Okk
sorry bro
Solution using only vectors (slices in Go) in a couple of words: 1. From l, r, a, b we build segment l, b and add such pairs to slice as a segment 2. Sort the segments by start coordinate 3. Use scanline to get union of segments as a new set of segments (which is already sorted as well) 4. For each query use binary search (sort.Search is very convenient in Go) on this new set and if the point is inside a segment, then the answer is the end coord of this segment
Here is the solution in C++, which is easily convertable to Go: https://mirror.codeforces.com/contest/1859/submission/218541082
could you please explain what "scanline" is in brief? I'm finding it difficult to understand why we're processing l, r, b in a particular order (not necessarily in that order). Thanks in advance
You don't need any fancy data structures to solve D. You just need to be able to sort the portals with respect to b 218826757, and thats about it.
Problem C can be done in linear time as well. Notice the ans is always of the Patten 1,2,3...k, n, n-1, n-2...n-k type. For example, for n=10, it is 1 2 3 4 5 10 9 8 7 6. So just try all such for given n and return maximum. I wonder why constraints where so low. With above approach, we can easily solve for higer N also.****
Is there a proof for it?
how linear time? How do you find k without iterating N times?
Minus delta :(. Btw fast editorial.
thanks for editorial!
Problem C can be solved in O(n^2). The idea is to reverse some suffix of the sorted permutation and finding which gives maximum power. 218547871
Try to prove that)
pattern recognition forces
Nah only C was pattern (and it was also unintended, the actual solution looks very legit)
Yeah, I agree it was a good problem
Problem C can be solved in O(n^2+t*n).We can preprocess an array first and calculate it easily. My English is a little poor. You can see https://mirror.codeforces.com/contest/1859/submission/218569933 .
Can you prove it is correct?
My solution to the problem D (it can be easier to understand for someone).
First of all, we can use only $$$l_{i}$$$ and $$$b_{i}$$$ ('cause it is always beneficial to teleport to point $$$b_{i}$$$, and we do not really need to teleport to the point $$$b_{i}$$$ from the right)
So let's say we have got $$$n$$$ segments $$$l_{i}, b_{i}$$$. If two segment intersect each other we can squeeze them (we can do it by using simple stack)
After we squeeze all of the segment for each $$$x$$$ we just have to find the segment with the biggest $$$l$$$, which is not bigger than $$$x$$$ (we can do it by using binary search). After finding the segment the answer for $$$x$$$ will be max (x, $$$r_{i}$$$).
It takes $$$O((q+n)log(n))$$$ time.
btw, thanks for the fast tutorial!
I do the same .I think this is the best soln that can be possible After reliazing that [l1..b1] range is sufficient , its rating is like div2B :))
yup , I did this same way submission
What if a,b is not inside l,r
still waiting on someone to prove why th does 1 2 3 k n-1 n-2 k+1 solution for C works i just noticed it while using next permutation and find the biggest possible answer
I love this Round. Because I can learn a lot from it. Thank you!
Are questions like c really relevant . Meaning which ability of ours is it testing.
The time limit was very strict for Problem D it seems.. Another nlog n solution with lazy segment tree got TLE... https://mirror.codeforces.com/contest/1859/submission/218564665 :-(
I solved it with segment tree as well and I get TLE on test case 9 though without lazy. If I added lazy I would also have the same result as you. I agree with you this was very strict. Maybe the author didn't even notice that there is a solution with segment tree. What would have been most optimal would be to split this task into 2 parts one getting 1500 points and the other 250 points and just say that the time limit is the only difference. Put 3 seconds on the easy version and 2 seconds on the hard version. If I have done all the correlation steps to achieve O( NlogN + QlogN ) complexity why should I get a big fat 0?
yea correct.. seems the author and tester didnt notice the segmentree solution.. the code passes in g++20 actually.. :-(
Like if they put the limit to be 3 seconds I don't see how a quadratic solution would pass anyways... It's a bit ridiculous if you ask me how they came up with 2 seconds as the time limit. I guess they just timed their solution and that was it.
What's even more pitiful is that it doesn't really take much skill to switch from a segment tree solution to a PQ solution for this problem. It's the same observations that you need to make essentially and simply apply them using the respective container.
But in any case: This can be a lesson for both you and me to always
1) Check first if a segment tree solution can be easily changed to a PQ or iterative seg tree one. 2) Always submit as g++20 since we have already seen in many cases where the same code passes in g++20 and not in previous compiler versions.
Hi!
Sorry that this happened, we did not want to cut off such solutions. One of our testers passed two segment trees, one with lazy operations and one without, so we thought that the TL was OK.
I will try to be more lenient with TL's from now on.
i got tle with segment tree beats at first too, then changed to set but still got tle because for convenience i substituted an array for std::map??? complexity's still right but i got stuck for a long time...
Can anyone help me with my solution of Task D I am getting TLE on test case 9 although my time complexity is qlog(n)??
Thanks for the great round and nice hint based editorial !
Here is my advice about the problems I solved:
Perfect problem A! There is an idea, it is not an A + B problem. The statement is short.
Perfect problem B!! I think that creating a good B is extremely hard because it has to be easy to implement, there should be some idea that is not completely obvious but still a bit obvious... The problem is interesting and fun to solve!
The problem by itself is cool but I think that the time limit is a bit too extreme. I came up with an $$$O(N^3 log(n))$$$ solution directly which got TLE so I spent 30mn optimising it to $$$O(N^3)$$$. I think it could have been better to clearly draw the line and ask for an $$$O(N^2)$$$ algorithm. I also think that it is an issue to have a problem with an ""easy"" pattern to guess. The solve count is very high and it is most likely because people guessed the pattern without proving it. The problem is still great but I think that such factors (is the problem guessable) should be considered, especially when setting a problem that everyone will read (if it was a "guessable" div2F, it would be fine because not that much people will actually try to guess it). I'm interested in the advice of other people about this problem. Maybe it is actually fine to have ""guessable"" problems, I don't know.
I find it very funny that this problem has a large variety of solutions ! I think that it is a bit standard but the problem is still enjoyable to solve and educative. I think that every round can have at most one or two such "educative" problems. What are your thoughts about this?
Again, nice trick about handling |a — b|. It helps in a lot of other problems such as 1622E - Math Test so it's a problem that actually teach some "general" ideas which is great.
Thanks for the contest! Feedback on the problems:
A: Good easy problem.
B: Fine easy problem.
C: Decent problem; not terrible but not my favorite. I think the problem would have been better with a higher time limit--I don't think there's much risk of a brute force solution passing and I think it would have been better to clearly accept $$$O(N^3 \log N)$$$ rather than making its result implementation-dependent (my straightforward implementation gets AC in 2800ms without the optimization mentioned in the editorial). I could imagine using either ~5s or 1s, with 1s intended to clearly cut all solutions that don't optimize out the log factor. Especially because the slower solution requires some optimization to get AC, I don't love that there is also an $$$O(N^2)$$$ solution that seems pretty difficult to prove, since this pretty heavily rewards proofs by AC.
D: Good problem, probably my favorite of the round. The observation that the containment constraint is helpful is pretty nice and the implementation is fairly straightforward from there. (The bonus task is also nice, and I thought about it in-contest when I didn't read the containment constraint--I could imagine including it as a harder subtask with a score distribution along the lines of 1500 + 2500, but I think excluding it is fine too.)
E: Good problem; the absolute value maximization trick is a nice one for people who haven't seen it yet.
I don't understand why my solution gets AC: see here for my in-contest solution and here for the solution I think is correct. The difference occurs in case 4; I think my current solution maximizes |A[l] — A[r]| + |B[l] — B[r]| instead of |A[l] — B[r]| + |A[r] — B[l]| when the interval we choose has length greater than one. I have no idea why this passes, but at the same time I don't immediately see a countercase (it's a bit harder because I correctly handle the case where the length of an interval is 1).
My current theory is that the only two cases we need to actually consider are A[l] + B[l] — A[r] — B[r] and A[r] + B[r] — A[l] — B[l]; for the other two cases we could do better by splitting into smaller intervals. Indeed, this submission only considers these two cases and gets AC. If anyone has a proof of this, I'd be happy to see it; I'll also try to show that this holds myself later on.
F: Fairly good problem. The implementation was a bit annoying, but that's hard to avoid unless you want to exclude this type of heavy-duty tree problem entirely.
My one criticism of the statements is that I think "cost" should be replaced with "value" in C and E. Typically, we try to minimize a cost, so when I skimmed the problems and read the word "cost", I tried to minimize the answers rather than maximizing them for my first few minutes. I think it makes more sense to use cost for minimization problems and value (or e.g. score or similar) for maximization problems.
Overall, though, I enjoyed the contest--thanks very much to the authors!
Geothermal Your intuition on E is correct! In fact, for the other two cases, you can do better by simply considering the singleton intervals at the endpoints.
The only two cases we need to actually consider (for intervals of size at least two) are $$$A[l]+B[l]—A[r]—B[r]$$$ and $$$A[r]+B[r]—A[l]—B[l]$$$.
We can rephrase the claim as the only cases we need to consider are the "dually monotonic" ones:
Suppose for a contradiction that there exists some optimal interval where the above doesn't hold and there is an "inversion". We will show that considering only the two singleton intervals at the endpoints gives equal or better value ($$$=2*|B[r]-A[r]|+2*|B[l]-A[l]|$$$).
WLOG, $$$A[l]$$$ is the smallest element. Then there are 4 cases to consider:
$$$A[l]<=A[r]<=B[l]<=B[r]$$$. In this case, the value is $$$(B[r]-A[l])+(B[l]-A[r])=(B[r]-A[r])+(B[l]-A[l])<= singleton$$$
$$$A[l]<=A[r]<=B[r]<=B[l]$$$. Analogous.
$$$A[l]<=B[r]<=B[l]<=A[r]$$$. In this case, the value is $$$(B[r]-A[l])+(A[r]-B[l]) \leq (B[r]-A[r])+(B[l]-A[l])+3*(B[r]-B[l])+(A[r]-A[l]) = 2*(A[r]-B[r])+2*(B[l]-A[l]) = singleton $$$
$$$A[l]<=B[r]<=A[r]<=B[l]$$$. Analogous.
For the only two cases that we now (provably) care about, both $$$|A[l] — A[r]| + |B[l] — B[r]|$$$ and $$$|A[l] — B[r]| + |A[r] — B[l]|$$$ are equivalent! So maximizing either gives AC :)
Wow, that's cool. We did not notice this during testing, thank you very much for your insight!
Regarding E: We can show that if A[l] — B[r] >= 0 and A[r] — B[l] >= 0 (one of the mixed case from above), it is always better to use two singletons instead of using a single interval of length > 1. Label the four numbers A[l], A[r], B[l], B[r] as x1, x2, x3 and x4 according to their order, i.e. x1 <= x2 <= x3 <= x4. There are six ways to arrange them such that the inequalities hold. I will discuss 2 of them:
For the first case we have (cost of the interval on the left, cost of the singletons on the right):
x2 - x1 + x4 - x3 <= 2x3 - 2x2 + 2x4 - 2x1because after simplification we have:
0 <= x4 + 3x3 - 3x2 - x1For the second case we have:
x3 - x1 + x4 - x2 <= 2x3 - 2x2 + 2x4 - 2x10 <= x4 + x3 - x2 - x1We can verify the inequality holds for all other cases in a similar way.
Thanks for the proofs, y'all! I forgot that the objective function is nonnegative in $$$k$$$, so I was trying to do something more complicated involving breaking the sequence into two parts whose union is the entire sequence. Using the singletons makes this very clean; nicely done!
I solved problem C in O(n2) by 1, 2, 3, ..... n, n-1, ....., x. But idk how to prove it >:(, just wasted 1 hr.
Thanks for the great contest, really enjoyed it. Hope I will turn green today :)
to C
define $$$k=n-\lfloor \sqrt{2n+1} \rfloor$$$
for
1~k, $$$p_i=i$$$for
k+1~n, $$$p_i=n+k+1-i$$$so C can be solved in $$$O(n)$$$
any proof you have for that?
I just find the pattern by running my $$$O(n^2)$$$ program.
It seems to be correct,but i can't prove it.
Please help me find out why I get the wrong answer in B pretest 4 please don't downvote, I'm trying for hours but couldn't find why I get WA.
Ok, so here is my code
Note that due to the bounds given in the task, the maximum sum is about $$$25000 \cdot 10^9 \approx 2 \cdot 10^{13}$$$, which is outside the usual valid range for
int(up to ~$$$10^9$$$).OMG, thank you so much.
I'm new to C++, I used Python before and didn't have to worry about using ints or longs lol.
Why my solution gives TLE on problem E.
Looks like you’re unnecessarily memset-ing the entire dp table every time instead of only up to N, which could be slow.
I removed memset and did the same manually Accepted solution, why it works now? Can you please explain. Thanks btw. :)
Before you were filling the entire MAXN (3000) dp table everytime which is too slow, instead of filling only up to n for that test case
Problem C can be solved in O(NlogN) too. If you look carefully at the given test cases, all the solutions are obtained through reversing a suffix of the sequence
1 2 3 4 ... n. So it was deducible that the best possible answer will have a certain suffix reversed, but which suffix ? For that I calculated value of(∑ni=1pi⋅i)−(maxnj=1pj⋅j)for all possible suffix reversed sequences. Here is a simulation for n = 11:Notice that plotting the values
(∑ni=1pi⋅i)−(maxnj=1pj⋅j)against the starting number(position) of the suffix reversed we get a Bitonic function!Thus all we needed to find was the beginning of the suffix for the largest answer, or more simply the bitonic point, which can be done in log N time using binary search.
Here's my solution(218593697) for problem C.(I didn't even look at the time limit given and assumed it to be <= 1 second based on the constraints. Thus, spend unnecessary time on this optimized solution).
I was trying to solve problem D with dsu, but I was missing an important part of the algorithm. Can someone tell me if it's possible to determine does point X belongs to some of N segments in O(log N) or O(1). Thank you in advance
1) Yes, it can be done. Let's sort all segments $$$(l;r)$$$ with condition $$$l_{i} \le l_{j}$$$ for $$$i \le j$$$. Ok, now we can do this by binary search:
Let's find position $$$i$$$ with maximum $$$l_i$$$ with condition $$$l_{i} \le x$$$. For all $$$1 \le j \le i$$$ now condition $$$l_j \le x$$$ is correct. Let's just find maximum value $$$r_j$$$ on prefix $$$[1;i]$$$, and if $$$r_j \ge x$$$ result is YES.
2) In this problem, we have offline queries, we can create event-type algorithm to calculate answer for all values $$$x$$$ in $$$\mathcal{O}(n\log{n})$$$.
for problem D, I tried representing each portal as a vertex and then found all connected components in the resulting graph, which consists of edges between vertices with overlapping ranges. I couldn't get AC. Did anyone try using this approach and how did you do it? Thanks!
I actually thought of this too and I also failed lol
Isn't graph will be too large? With $$$n$$$ vertex number of edges will be up to $$$\frac{n(n-1)}{2}$$$
Since it can be observed that $$$r_i$$$ and $$$a_i$$$ are useless for each segment. I use $$$l_i$$$ to sort all segments($$$l_i; b_i$$$) and then use some kind of greedy to merge all intersecting segments. Then I only need to use binary search for each $$$x_i$$$ to find which segment is covering it.
Although my approach isn't the same as yours, I hope it'll be useful for you. Here's my code:218556118.
C question can be solved in O(n) runtime. I noticed from the test cases that first, say k, elements of the permutation would be same as the index and the remaining n-k elements will be in reverse order of the remaining indices. i.e., the array will be 1,2,3,...,k-1,k,n,n-1,....,k+1. So we can just run a loop to see for what value of k the cost is maximized. As simple as that!
No it's O(n) only. For any k, you can write a mathematical expression for the sum of last n-k elements instead of looping through it. Also to find the max element, it will be the middle element of last n-k elements, which can be done in constant time. Check out my solution at https://mirror.codeforces.com/contest/1859/submission/218596825.
is it possible for you to post a proper Mathematical proof for this series sum which then can be done in O(1) for every k.
my bad, I didn't think about formula
IN problem B shouldn't the minimums be moved to array with smallest difference between second smallest and its minimum element rather than to smallest second smallest element????????????????????????
No. Consider the case with two arrays $$$[1, 3]$$$ and $$$[3, 4]$$$. Your solution would suggest moving minimums to the second array leading to arrays $$$[3]$$$ and $$$[1, 3, 4]$$$ with $$$\mathrm{score} = 3 + 1 = 4$$$.
The correct solution would suggest moving minimums to the first array leading to arrays $$$[1, 1, 3]$$$ and $$$[4]$$$ with $$$\mathrm{score} = 1 + 4 = 5$$$ which is larger.
For problem E, the editorial says "Now we can look at out dp states as a table, and notice that we recalc over the diagonal". Does this mean one must look for patterns, or is there a way to notice this recalculation mathematically? Thanks in advance!
Basically, from dp(i,j) you are making a move to dp(i-1, j-1). Which is considered a diagonal move.
We can use Centroid Decomposition to solve problem F in $$$O(n\log n\log w)$$$.
Code: 218616904
It works faster than the common solution(with LCA).
That is cool.
It probably is due to the fact that the average centroid tree height is small, so you really do less operations constant-wise.
Thank you very much for this cool submission!
C can be done in O(1). It is a straightforward formula, that can be derived with a bit of paperwork. We can prove by induction that for every n, the max cost can be found by reversing the last 'k' digits while writing 1 to n in ascending order. Eg- 1 2 3 4 5 6 10 9 8 7{max cost case of n=10}. So if we consider the general case, cost = (1^2+2^2+...(n-k)^2)+{(n)(n+1-k)+(n-1)(n+2-k)....(n-k+1)(n)}-max((i from 1 to k)(n+1-i)(n-k+i)). max(i.e. the third term in above formula) can be calculated by AM>=GM. so the final expression of cost is cubic in terms of k, which is to be maximized by d(cost)/dk=0. thus we get a O(1) solution. you can check my submission to see the final formula{I don't know how to add the link}.
For problem D, there seems exists a $$$O(n)$$$ solution using dsu. Considering combining the interval $$$[l_i, b_i]$$$, and setting the ancestor of these elements to $$$b_i$$$. Consider 218626575.
Sorry for forgotting the time consumption of sorting, which costs $$$O(n\log n)$$$.
Two intervals are combined in a single set if they overlap. Can you explain how to construct dsu(specifically union)? Since there are n intervals, I'm performing O(n^2) comparisons to check whether two intervals overlap and perform union.
Sure. The fact is that cheking for overlapping of intervals may be unnecessary. We can just combine these overlapped intervals in a single set, which means that all beginners in the set can reach to the right-hand side endpoint of the interval.
Hey, here is my code for the problem E. The time complexity should be O(N*N), according to me. However, even if it is not the case, how can the program pass 21 tests and give a TLE on the 22nd test case? The passed cases already involve worst-case values (N=3000, K=3000).
Please let me know where I am going wrong.
Your solution is O(N^3). In general you have N^2 states and the transition from one state to another is done in O(N) in your memo function. If N = K there are only O(N) visited states since i = k for each. That's why it works on other test cases.
Thanks
I am weak in mathematical notation. I have solved problem D but do not understand tutorial. I don't understand the mathematical notation of this line "Let ansi be the maximum coordinate we can reach while being on segment i, and let pj be the answer to the j-th query. Then we notice that the answer to query pj=max(xj,maxni=1ansi|li≤xj≤ri)". Can you please explain this part "pj=max(xj,maxni=1ansi|li≤xj≤ri)". Thanks in advance.
Why does this code take 1500 ms?
Can someone explain why i am getting run time error in problem D. 218670993
How 2 prove my C's solution? QAQ Just enumerate every i from 1 to n, flip the last k numbers of an ascending sequence of 1 to n, compute each answer and arrive at the maximum value, the final answer.
I don't understand why it's correct even I Accepted D:
Here is a sketch of why the faster solution to C works:
First, consider permutations $$$1$$$, $$$2$$$, $$$\ldots$$$, $$$y-1$$$, $$$n$$$, $$$n-1$$$, $$$\ldots$$$, $$$y$$$. In this case, the answer is basically $$$1/12 (2 n^3 + 6 n^2 y - 3 n^2 - 6 n y^2 + 6 n y - 2 n + 2 y^3 - 9 y^2 + 4 y)$$$, the maximum occurs at around $$$y=n+1.5+\sqrt{2n+1}$$$, or $$$y=n+1-\lfloor\sqrt{2n+1}\rfloor$$$.
Let $$$x$$$ be the maximum of $$$jp_j$$$. Then, $$$ip_i\leq x$$$, $$$i\leq n$$$, and $$$p_i\leq n$$$ implies $$$i+p_i\leq n+\frac xn$$$. Let $$$C=n+\left\lfloor\frac xn\right\rfloor$$$. Consider the largest possible value of $$$\sum_{i=1}^n ip_i-x$$$ over all permutations satisfying $$$i+p_i\leq C$$$. By the observation in the editorial (local swapping arguments), the maximum occurs when $$$p_1=1$$$, $$$p_2=2$$$, $$$\ldots$$$, $$$p_{C-n-1}=C-n$$$, $$$p_{C-n}=n$$$, $$$\ldots$$$, $$$p_n=C-n$$$. In this case, we compute $$$\sum_{i=1}^nip_i-x\leq\frac16 (n^3 + 3 n^2 y - 3 n y^2 + 6 n y - n + y^3 - 3 y^2 + 2 y)-ny$$$ where $$$y=C-n=\left\lfloor\frac xn\right\rfloor$$$ since $$$ny\leq x$$$. This is less than the construction given above when $$$y\leq n-2\sqrt n$$$. When $$$y>n-2\sqrt n$$$, the optimal permutations are very easy to characterize: since the part of the hyperbola $$$ip_i\leq x$$$ where $$$1\leq i\leq n$$$ and $$$1\leq p_i\leq n$$$ is very close to a line with slope -1, you must have $$$p_1=1$$$, $$$p_2=2$$$, $$$p_a=a$$$, $$$p_{a+1}=b$$$, $$$p_{a+2}=n$$$, $$$p_{a+3}=n-1$$$, $$$\ldots$$$, $$$p_{a+1+n-b}=b+1$$$, $$$p_{a+2+n-b}=b-1$$$, $$$p_{a+3+n-b}=b-2$$$, $$$\ldots$$$, $$$p_{b-1}=a+n-b+2$$$, $$$p_b=a+1$$$, $$$p_{b+1}=a+n-b+1$$$, $$$\ldots$$$, $$$p_n=a+2$$$, which is easily verified to be optimal in the equality case above.
The details are left to the interested GM.
Hii, guys I am new to codeforces, can anyone please guide me why my sol failed on 4th pretest even though i used same aporach as author?
Link to sol — Your text to link here...
int main() { int n; cin>>n; for(int i=0;i<n;i++){ int n_arr; cin>>n_arr; vector<vector> v; for(int j=0;j<n_arr;j++){ vector temp; int sz; cin>>sz; for(int k=0;k<sz;k++){ int tp; cin>>tp; temp.push_back(tp); } sort(temp.begin(), temp.end()); v.push_back(temp); }
vector<int> abc; int mn = v[0][0]; for(int j=0;j<n_arr;j++){ mn = min(mn, v[j][0]); abc.push_back(v[j][1]); } sort(abc.begin(), abc.end()); int ans = mn; for(int j=1;j<abc.size();j++){ ans+=abc[j]; } cout<<ans<<endl; } return 0;}
Thank you for help!
Corrected You need to take the final sum as long long
O(log n) solution of C log factor is due to sqrt
218710354
How my $$$O(n^4)$$$ solution passed in C?
For Problem E, had the problem ask for the minimum instead of maximum, is it still possible to solve it given the constraints? Maybe I'm missing something obvious.
I'm attempting a proof for the C solution using pattern: $$$1,2,3,4, ... , x−1,n, n−1,n−2, ... , x$$$.
Please feel free to comment/add/correct/improve.
1.If $$$n$$$ is paired with $$$x$$$, then $$$x$$$ is paired with $$$n$$$.
Suppose $$$n\rightleftharpoons x$$$ and $$$n\rightleftharpoons y$$$ pairs exist, and $$$x$$$>$$$y$$$. The answer can be improved by swapping $$$n\rightleftharpoons y$$$ pair with $$$x\rightleftharpoons ?$$$ pair to give $$$n\rightleftharpoons x$$$ and $$$y\rightleftharpoons ?$$$.
Applies to the largest mixed-paired number, so not just $$$n$$$. This cuts out a lot of permutations.
2.Pairings do not cross.
If $$$a \rightleftharpoons b$$$ and $$$c\rightleftharpoons d$$$ pairings exist, then the range $$$(a,b)$$$ does not overlap with $$$(c,d)$$$.
Proof by comparing possible combinations. Can always better the crossed pairings. A bit messy.
3.If $$$n$$$ is paired with $$$x$$$, then $$$n-1$$$ has to be paired with $$$x+1$$$ (if $$$n-1>x+1$$$).
Given 1&2 above, $$$n-1$$$ has to be paired with a number larger than $$$x$$$. Suppose $$$n-1$$$ is paired with $$$y>x+1$$$, then the numbers in range $$$(x,y)$$$ will be paired to themselves as any pairing amongst them will lower answer; furthermore, answer could be improved by pairing $$$n$$$ to $$$y-1$$$ instead of $$$x$$$.
This can be extended to $$$n-2$$$ etc, if necessary. Of course, if $$$x$$$ is large, there might not be any need to pair $$$n-1$$$.
To summarise, if the optimal solution contain pairing $$$n \rightleftharpoons x$$$, then the given pattern would be the best.
jiangly's solution to problem C using DSU was also O(n^3) if not better. (I don't really understand amortised analysis at all).
After fixing $$$M$$$ and noticing that the greedy strategy of giving the highest available position to the numbers $$$n,n-1,...,1$$$ (in that order) is optimal, he used DSU to build the permutation in linear time.
For every n, the highest/rightmost position that satisfies that $$$p_i\cdot i$$$ will be $$$min(n,M/i)$$$.
If this highest position is available, then the value of its parent(as in DSU convention) is going to be itself and we can simply put $$$p \in P$$$ to this position. After doing so, we update its parent as the preceding position (via the merge/union operation). Doing this has the effect that, for all future elements that could have theoretically taken this position, are nudged to take the preceding position instead until they do find an empty position.
Overall, the idea was that we maintain the highest available position as the parent of the currently "formed" part of the permutation. So, whenever a theoretical rightmost position is pre-occupied, then the highest available position can be used up.
Implementation details: Omit union-by-rank/size heuristic because we want a very specific type of union such that we make the preceding position (even if it had a rank/size = 1 only) as the parent of a position we just filled up.
jiangly's submission 218527131
my submission (if useful to anybody) 218844879
UPD:: Afterthoughts, this is pretty much the same thing as the use of stack in the editorial. Complexity should be same/similar.
Why is this code giving TLE for Problem D. I used a different approach from the one given in the tutorial, but Time Complexity wise, it is still the same. I could optimise it as much as I could. Any thoughts?
O(N^2) solution for problem C. Link : SUBMISSION LINK
Idea : We will go for the following pattern - n=6
We will calculate answer for each and take maximum.
Can anyone explain the O(n^3) solution of problem C for me, I can't understand what the stack does there and can't figure out how it makes the time complexity to O(n) in the loop
Hi!
First we notice the solution which uses $$$std::set$$$, where we greedily pick the maximum available while iterating from $$$N$$$ to $$$1$$$.
Now let's do the following — we say that we can pair each number $$$k$$$ from $$$1$$$ to $$$N$$$ with the following prefix: $$$[1; \lfloor\frac{mx}{k}\rfloor]$$$, where $$$mx$$$ is the current maximum which we are iterating over. We can notice that we always pair the number with the highest available — so, for each index $$$i$$$ we create a vector of numbers which "become available" for all indexes $$$k \leq i$$$. Then we just use stack to maintain all available elements in descending order.
Can someone help me understand the optimisation in Que E?
Hi!
The idea is that $$$|x| = max(-x, x)|$$$, and we can use this to simply consider different cases of modulos instead of always doing it correctly.
After that we use a simple vector to store the maximum sum.
in D I did binary search + dfs (also it's kinda dp)
Hello,
I think in the editorial of the First Problem "United we stand", writer have missed to add "end of line", while displaying two arrays.