johnathan79717's blog

Another Viewpoint for Problem Manasa and Combinatorics on HackerRank
By johnathan79717, 11 years ago, In English

Manasa and Combinatorics is one of the problems in Ad Infinitum April'14. The problems are very interesting, and some mathematical insights are required. Thanks to Shashank Sharma for organizing the great competition.

Here is the upcoming Ad Infinitum May'14.

Someone sent me a message asking how I got the formula in this problem, so I figured why not post it somewhere for everyone to see.

The problem asks the number of strings consisting of N number of A's and 2N number of B's, without any prefix or suffix having more A's than B's.

The editorial can be found here, and as you can see in this pdf file, the formula in the code can be derived algebraically.

Here, I would like to provide another point of view, that is easier to visualize. (The following images are from here.)

Forgetting the constraint about prefixes and suffixes. What's the number of strings with N number of A's and M number of B's? The problem is equivalent to asking the number of different paths from P(0, 0) to Q(M, N), if you consider A as going up and B as going right. In the images M = 5 and N = 3. The answer is .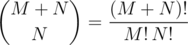

Now if we want every prefix to have no more A's than B's. The corresponding paths must not cross the green line (y = x), and hence not intersecting the red line (y = x + 1).

However, if a path intersecting the red line, the part before intersecting can always be reflected with respect to the red line, and be mapped to a path from P′( - 1, 1) to Q(M, N). Subtracting the number of paths intersecting the red line, we get that the number of strings with wrong prefixes is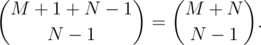

What about suffixes? You can rotate the grid 180 degrees and imagine another red line at the bottom right corner, and the original Q(M, N) is reflected similarly to Q′(M + 1, N - 1). Every path touching the bottom-right red line is mapped to unique path from P to Q′, so the number is again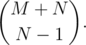

Finally, because of the inclusion-exclusion principle, we have to find the strings that have both wrong prefixes and suffixes. That's exactly the number of paths from P′( - 1, 1) to Q′(M + 1, N - 1)! Therefore, the formula is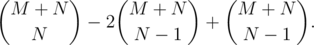

All that's left is calculate 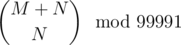for M, N ≤ 1012. You can use Lucas' theorem. Since I didn't know the theorem before reading the editorial, I used this formula to calculate a and e where N! = a × 99991e.

P.S. I also like the problem Ichigo and Cube very much.

  • Vote: I like it
  • +53
  • Vote: I do not like it

»
11 years ago, # |
← Rev. 5   Vote: I like it +6 Vote: I do not like it

I solved this problem in exactly the same way as you did. I wanted to add this solution to the editorial but it was quite complicated to explain. You did an excellent job with those diagrams. The editorial should probably contain a link to this blog post.

I actually completed the problem in a slightly different way. I feel bad because I know Lucas' theorem but didn't remember it when I saw what I had to compute. Moreover, Lucas' is made for exactly these kind of calculations :( Anyway, my approach was to use Legendre's theorem to check if the answer is divisible by p and if not, I discard all the 'p's in the prime factorization and repeatedly reduce the rest of the terms using Wilson's theorem. Relevant details in this code.

And I am the author of both the Ichigo problems, thanks a lot for your comments :D

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 3   Vote: I like it +6 Vote: I do not like it

    I think I compute the binomial coefficient the same way you did. The link I posted was too complicated, but is essentially the same as your method. Thank you and other setters for these amazing problems :)

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Please can you re-upload the images if you can???The question and Your explanation are quite nice :)

→ Reply