Автор: Friendiks
Больше про алгоритмы в ТГ канале: https://t.me/KogutIvanTutoring
Пререквизиты
Дерево отрезков, merge sort(сортировка слиянием)
Вступление
Для начала решим такую задачу:
Дан массив размера $$$n$$$, а также $$$q$$$ запросов вида: количество различных элементов на отрезке от $$$l$$$ до $$$r$$$ ($$${l, r} \le n$$$). Для данной задачи существует решение через персистентное дерево отрезков, но его рассматривать мы не будем. Рассмотрим другое решение. Для начала для каждого элемента найдем индекс ближайшего равного ему справа, а если такого нет, поставим большое число(в нашем случае $$$10^9+7$$$, но главное, чтобы оно было больше $$$n$$$) и построим новый массив, который хранит вместо элемента данный найденный индекс(или большое число). Тогда можно заметить, что количество различных чисел на отрезке $$$[l, r]$$$ — это количество чисел на отрезке в новом массиве, больших $$$r$$$. Упражнение для читателя — понять почему это так ;)
Теперь надо научиться искать количество больших на отрезке. Воспользуемся структурой данных Merge Sort Tree.
Merge sort tree
Идея merge sort tree заключается в том, чтобы построить дерево отрезков и в каждой вершине хранить отсортированный отрезок покрытый вершиной. Несложно заметить, что для каждой вершины массивы в ее детях отсортированы и поэтому можно применить слияние как в merge sort и за $$$O(st[l].size()+st[r].size())$$$ получить то, что нам надо. Пример кода для пересчета приведен ниже.
st.resize(st[l].size()+st[r].size()) // размер должен быть равен итоговому размеру, иначе функция merge выдаст ошибку
merge(st[l].begin(), st[l].end, st[r].begin(), st[r].end, st[v].begin())
// v - текущая вершина, l - левый сын, r - правый сын.
// st - вектор, хранящий дерево отрезков
На первый взгляд, кажется, что асимптотика построения и занимаемая память это $$$O({n^2 \log n}$$$), но на самом деле достаточно понять, что каждый элемент массива будет находиться в $$$O(\log n)$$$ отрезках. На каждой высоте мы учтем элемент ровно 1 раз, а так как высота дерева отрезков $$$O(\log n)$$$, то и каждый элемент будет учтен в $$$O(\log n)$$$ отрезках. Из этого можно сделать вывод, что на самом деле асимптотика построения merge sort tree и занимаемая им память $$$O({n \log n})$$$.
Решение задачи с помощью merge sort tree за $$$O({n \log n} + {q \log^2 n})$$$
Решим задачу используя эту структуру. Теперь мы можем дойти до каждой вершины, такой, что она покрывает отрезок, который полностью лежит в отрезке запроса, а потом бинарным поиском найти количество больших $$$r$$$. Как известно, любой отрезок разбивается на $$$O({\log n})$$$ отрезков дерева отрезков, а также бинарный поиск работает за $$$O({\log n})$$$, а значит мы умеем отвечать на запрос за $$$O({\log^2 n})$$$.
Эта асимптотика уже очень хорошая, но можно сделать лучше, и в этом поможет Техника Частичного Каскадирования.
Решение задачи с помощью merge sort tree и техники частичного каскадирования за $$$O({n \log n} + {q \log n})$$$
Основная идея техники частичного каскадирования заключается в том, чтобы заранее предпосчитать для каждого числа в массиве вершины первое большее либо равное число в левом сыне и первое большее либо равное число в правом сыне. Сделать это можно линейным проходом по массиву вершины и поддержанием двух указателей на нужный элемент в левом и правом сыне. Пример кода, который это делает приведен ниже.
st[v].resize(st[l].size()+st[r].size());
cascad[v].resize(st[l].size()+st[r].size());
merge(st[l].begin(), st[l].end(), st[r].begin(), st[r].end(), st[v].begin());
int i = 0, j = 0;
for(int k = 0; k < st[v].size(); ++k){
while(i < (int)st[l].size() && st[l][i] < st[v][k]) i++;
while(j < (int)st[r].size() && st[r][j] < st[v][k]) j++;
cascad[v][k] = make_pair(i,j);
}
Теперь можно заметить, что для ответа на запрос нужно в корне найти бинарным поиском первый больший либо равный $$$r$$$ (если пишите дерево отрезков на полуинтервалах, а иначе надо искать строго больший). Обозначим найденный элемент за $$$x$$$. Если отрезок лежит не полностью, то при переходе в левого(или правого) ребенка можно передавать $$$x$$$ для ребенка, он будет равен cascad[v][x].first(или second). Иначе, если отрезок полностью лежит в запросе, ответом будет $$$st[v].size() - x$$$ (если считать, что индексы нумеруются с нуля). Можно заметить, что если все элементы меньше, то написанный выше while вернет размер массива и все сработает корректно. Не сложно заметить, что суммарно ответ на запрос теперь работает за $$$O({\log n})$$$, а значит мы решили задачу за $$$O({n \log n} + {q \log n})$$$.
Задачи
https://mirror.codeforces.com/group/on4GqeQ4Du/contest/328897/problem/I
https://mirror.codeforces.com/group/on4GqeQ4Du/contest/328897/problem/H
https://informatics.msk.ru/mod/statements/view3.php?chapterid=113732#1
Время работы на практике
Несмотря на то, что с каскадированием асимптотика получается лучше чем без каскадирования, но на практике с каскадированием программа работает дольше чем без него. 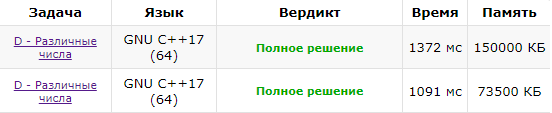
Нижняя посылка — без каскадирования, а верхняя с каскадированием.
Спасибо за это замечание CtrlAlt
Дополнительно
- Merge sort tree также может использоваться для поиска k-ой порядковой статистики за $$$O({\log^3 n})$$$ без каскадирования за запрос и за $$$O({\log^2 n})$$$ с каскадированием.
- Если вместо массивов использовать декартовы деревья, то можно будет изменять элементы за $$$O({\log^2 n})$$$, но придется отказаться от каскадирования.











Автокомментарий: текст был обновлен пользователем Kogut_Ivan (предыдущая версия, новая версия, сравнить).
Для связности:
По наблюдениям, время работы решений с частичным каскадированием хуже, чем без него (несмотря на лучшую асимптотическую оценку).
Автокомментарий: текст был обновлен пользователем Friendiks (предыдущая версия, новая версия, сравнить).