Hello, everyone!
We hope you like our problems!
Thank you for participation!
Author: ooaa
The stability of the wall is the number of horizontal bricks minus the number of vertical bricks. Since a horizontal brick has a length of at least $$$2$$$, no more than $$$\lfloor\frac{m}{2}\rfloor$$$ horizontal bricks can be placed in one row. Therefore, the answer does not exceed $$$n \cdot \lfloor\frac{m}{2}\rfloor$$$. On the other hand, if horizontal bricks of length $$$2$$$ are placed in a row, and when $$$m$$$ is odd, the last brick has a length of $$$3$$$, then in each row there will be exactly $$$\lfloor\frac{m}{2}\rfloor$$$ horizontal bricks, and there will be no vertical bricks in the wall at all. This achieves the maximum stability of $$$n \cdot \lfloor\frac{m}{2}\rfloor$$$. The solution is one formula, so it works in $$$O(1)$$$ time.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int64_t n,m;
cin >> n >> m;
cout << n*(m/2) << '\n';
}
return 0;
}
Author: ace5
Notice that by performing operations of the form: swap $$$a_i$$$ with $$$a_j$$$ and $$$b_i$$$ with $$$b_j$$$ simultaneously, we can rearrange the array $$$a$$$ how we want, but the same $$$a_i$$$ will correspond to the same $$$b_i$$$ (because we are changing both $$$a_i$$$ and $$$b_i$$$ at the same time). Let's sort the array $$$a$$$ using these operations. Then the sum of the number of inversions in $$$a$$$ and $$$b$$$ will be the number of inversions in $$$b$$$, since $$$a$$$ is sorted. It is claimed that this is the minimum sum that can be achieved.
Proof: Consider two pairs of elements $$$a_i$$$ with $$$a_j$$$ and $$$b_i$$$ with $$$b_j$$$ ($$$i$$$ < $$$j$$$). In each of these pairs, there can be either $$$0$$$ or $$$1$$$ inversions, so among the two pairs, there can be $$$0$$$, $$$1$$$, or $$$2$$$ inversions. If there were $$$0$$$ inversions before the operation, then there will be $$$2$$$ after the operation; if there was $$$1$$$, then there will still be $$$1$$$; if there were $$$2$$$, then it will become $$$0$$$. If the permutation $$$a_i$$$ is sorted, then in each pair of indices $$$i$$$ and $$$j$$$ there will be a maximum of 1 inversion, so any pair of indices will give no more inversions than if they were swapped. Since the number of inversions in each pair is the minimum possible, the total number of inversions is also the minimum possible.
Time complexity: $$$O(n \log n)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
pair<int,int> ab[n];
for(int i = 0;i < n;++i)
{
cin >> ab[i].first;
}
for(int i = 0;i < n;++i)
{
cin >> ab[i].second;
}
sort(ab,ab+n);
for(int i = 0;i < n;++i)
{
cout << ab[i].first << ' ';
}
cout << "\n";
for(int i = 0;i < n;++i)
{
cout << ab[i].second << ' ';
}
cout << "\n";
}
}
Author: ace5
Let's consider the bitwise representation of numbers $$$a$$$, $$$b$$$, $$$x$$$. Let's look at any $$$2$$$ bits at the same position in $$$a$$$ and $$$b$$$, if they are the same, then regardless of what is in $$$x$$$ on this position, the number $$$|({a \oplus x}) - ({b \oplus x})|$$$ will have a $$$0$$$ at this position. Therefore, it is advantageous to set $$$0$$$ at all such positions in $$$x$$$ (since we want $$$x \leq r$$$, and the answer does not depend on the bit). If the bits in $$$a$$$ and $$$b$$$ at the same position are different, then at this position there will be a $$$1$$$ either in $$$a \oplus x$$$ or in $$$b \oplus x$$$ depending on what is at this position in $$$x$$$.
Let $$$a$$$ < $$$b$$$, if not, then we will swap them. Then at the highest position, where the bits differ, there is a $$$0$$$ in $$$a$$$ and a $$$1$$$ in $$$b$$$. There are $$$2$$$ options, either to set a $$$1$$$ at this position in $$$x$$$ (and then there will be a $$$1$$$ in $$$a \oplus x$$$), or to set a $$$0$$$ in $$$x$$$ (and then there will be a $$$0$$$ in $$$a \oplus x$$$).
Suppose we set $$$0$$$ in $$$x$$$, then $$$a \oplus x$$$ will definitely be less than $$$b \oplus x$$$ (because in the highest differing bit, $$$a \oplus x$$$ has $$$0$$$, and $$$b \oplus x$$$ has $$$1$$$). Therefore, it is advantageous to set $$$1$$$ in $$$a \oplus x$$$ on all next positions, as this will make their difference smaller. Therefore, we can go through the positions in descending order, and if the position is differing, then we will set a $$$1$$$ in $$$a \oplus x$$$ at this position if possible (if after this $$$x$$$ does not exceed $$$r$$$).
The second case (when we set $$$1$$$ in $$$x$$$ at the position of the first differing bit) is analyzed similarly, but in fact it is not needed, because the answer will not be smaller, and $$$x$$$ will become larger.
Time complexity: $$$O(\log 10^{18})$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
const int maxb = 60;
bool get_bit(int64_t a,int i)
{
return a&(1ll<<i);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int64_t a,b,r;
cin >> a >> b >> r;
int64_t x = 0;
bool first_bit = 1;
if(a > b)
swap(a,b);
for(int i = maxb-1;i >= 0;--i)
{
bool bit_a = get_bit(a,i);
bool bit_b = get_bit(b,i);
if(bit_a != bit_b)
{
if(first_bit)
{
first_bit = 0;
}
else
{
if(!bit_a && x+(1ll<<i) <= r)
{
x += (1ll<<i);
a ^= (1ll<<i);
b ^= (1ll<<i);
}
}
}
}
cout << b-a << "\n";
}
}
Author: ace5
Let's do a binary search. Suppose we know that the minimum possible cost is at least $$$l$$$ and not greater than $$$r$$$. Let's choose $$$m = (l+r)/2$$$. We need to learn how to check if the answer is less than or equal to $$$m$$$. We will calculate $$$dp_i$$$–the minimum sum of blocked elements in the prefix up to $$$i$$$ if position $$$i$$$ is blocked, and on each of the subsegments without blocked elements, the sum of elements is less than or equal to $$$m$$$. Then $$$dp_i = a_i + \min(dp_j)$$$ for all $$$j$$$ such that the sum on the subsegment from $$$j+1$$$ to $$$i-1$$$ is less than or equal to $$$m$$$. Such $$$j$$$ form a segment, since $$$a_j$$$ is positive. We will maintain the boundaries of this segment. We will also maintain all $$$dp_j$$$ for $$$j$$$ inside this subsegment in the set. When moving from $$$i$$$ to $$$i+1$$$, we will move the left boundary of the subsegment until the sum on it becomes less than or equal to $$$m$$$, and remove $$$dp_j$$$ from the set, and also add $$$dp_i$$$ to the set. The minimum sum of blocked elements under the condition that the sum on all subsegments without blocked elements is less than or equal to $$$m$$$ can be found as the minimum among all $$$dp_i$$$ such that the sum from $$$i$$$ to $$$n$$$ is less than or equal to $$$m$$$. If this answer is less than or equal to $$$m$$$, then the answer to the problem is less than or equal to $$$m$$$, otherwise the answer is greater than $$$m$$$.
Time complexity: $$$O(n \log n \log 10^9)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
int64_t a[n+1];
for(int i = 0;i < n;++i)
{
cin >> a[i];
}
int64_t l = 0,r = int64_t(1e9)*n;
while(l < r)
{
int64_t m = (l+r)/2;
set<pair<int64_t,int>> pos;
int64_t dp[n+1];
int p2 = n;
dp[n] = 0;
pos.insert({dp[n],n});
int64_t sum = 0;
for(int j = n-1;j >= 0;--j)
{
while(sum > m)
{
sum -= a[p2-1];
pos.erase({dp[p2],p2});
p2--;
}
dp[j] = pos.begin()->first + a[j];
pos.insert({dp[j],j});
sum += a[j];
}
sum = 0;
int yes = 0;
for(int j =0;j < n;++j)
{
if(sum <= m && dp[j] <= m)
yes = 1;
sum += a[j];
}
if(yes)
r = m;
else
l = m+1;
}
cout << l << "\n";
}
}
Author: ace5
Randomized solution: We will use the quicksort algorithm. We will choose a random element from the array, let its index be $$$i$$$, and we will perform $$$?$$$ $$$i$$$ until we get the answer $$$=$$$ (i.e., $$$x = a_i$$$). Now we will ask about all the other elements, thereby finding out whether they are greater than or less than $$$a_i$$$ (don't forget to return $$$x = a_i$$$, i.e., perform $$$?$$$ $$$i$$$ after each query about the element). After this, we will divide all the elements into two parts, where $$$a_i > x$$$ and $$$a_i < x$$$. We will recursively run the algorithm on each part. The parts will become smaller and smaller, and in the end, we will sort our permutation, allowing us to guess it.
Non-randomized solution: We will find the element $$$1$$$ in the array in $$$3n$$$ queries. To do this, we will go through the array, asking about each element each time. If the answer is $$$<$$$, we will continue asking until the answer becomes $$$=$$$, and if the answer is $$$=$$$ or $$$>$$$, we will move on to the next element. Then the last element on which the answer was $$$<$$$ is the element $$$1$$$. $$$x$$$ will increase by a maximum of $$$n$$$ in the process (a maximum of $$$1$$$ from each element), so it will decrease by a maximum of $$$2n$$$, i.e., a maximum of $$$3n$$$ queries. Similarly, we will find the element $$$n$$$. Now we will run an algorithm similar to the randomized solution, but now we can set $$$x = n/2$$$ instead of taking $$$x$$$ as a random element.
Both solutions comfortably fit within the limit of $$$40n$$$ queries.
#include <bits/stdc++.h>
using namespace std;
mt19937 rnd(593);
char query(int i)
{
cout << "? " << i+1 << endl;
char c;
cin >> c;
return c;
}
void quicksort(vector<int> &a,vector<int> &ord)
{
if(a.size() == 0)
return ;
int mid = rnd()%a.size();
while(query(a[mid]) != '=')
;
vector<int> l,r;
for(int i = 0;i < a.size();++i)
{
if(i == mid)
continue;
if(query(a[i]) == '<')
{
l.push_back(a[i]);
}
else
{
r.push_back(a[i]);
}
query(a[mid]);
}
vector<int> l_ord;
vector<int> r_ord;
quicksort(l,l_ord);
quicksort(r,r_ord);
for(int i = 0;i < l_ord.size();++i)
{
ord.push_back(l_ord[i]);
}
ord.push_back(a[mid]);
for(int i = 0;i < r_ord.size();++i)
{
ord.push_back(r_ord[i]);
}
return ;
}
int main()
{
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
vector<int> a;
vector<int> ord;
for(int i = 0;i < n;++i)
{
a.push_back(i);
}
quicksort(a,ord);
cout << "! ";
vector<int> ans(n);
for(int i = 0;i < n;++i)
{
ans[ord[i]] = i;
}
for(int i = 0;i < n;++i)
{
cout << ans[i]+1 << ' ';
}
cout << endl;
}
}
#include <bits/stdc++.h>
using namespace std;
char query(int pos)
{
cout << "? " << pos << endl;
char ans;
cin >> ans;
return ans;
}
void dnq(int l,int r,vector<int> pos,vector<int> & res,int pos1,int posn)
{
int m = (l+r)/2;
vector<int> lh;
vector<int> rh;
for(int i = 0;i < pos.size();++i)
{
char x = query(pos[i]);
if(x == '>')
{
rh.push_back(pos[i]);
query(pos1);
}
else if(x == '<')
{
lh.push_back(pos[i]);
query(posn);
}
else
{
res[pos[i]] = m;
}
}
if(lh.size() != 0)
{
int m2 = (l+m-1)/2;
for(int j = 0;j < m-m2;++j)
query(pos1);
dnq(l,m-1,lh,res,pos1,posn);
query(posn);
}
if(rh.size() != 0)
{
int m2 = (m+1+r)/2;
for(int j = 0;j < m2-m;++j)
query(posn);
dnq(m+1,r,rh,res,pos1,posn);
}
return ;
}
int main()
{
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
int pos1 = -1;
for(int i = 1;i <= n;++i)
{
char ans = query(i);
if(ans == '<')
{
i--;
}
else if(ans == '=')
{
pos1 = i;
}
else
{
if(pos1 != -1)
{
query(pos1);
}
}
}
int posn = -1;
for(int i = 1;i <= n;++i)
{
char ans = query(i);
if(ans == '>')
{
i--;
}
else if(ans == '=')
{
posn = i;
}
else
{
if(posn != -1)
{
query(posn);
}
}
}
vector<int> res(n+1);
vector<int> pos(n);
for(int j = 0;j < n;++j)
pos[j] = j+1;
int m = (1+n)/2;
for(int k = 0;k < n-m;++k)
{
query(pos1);
}
dnq(1,n,pos,res,pos1,posn);
cout << "! ";
for(int j = 1;j <= n;++j)
cout << res[j] << ' ';
cout << endl;
}
}
Author: ooaa
First, it can be noticed that it is enough to visit all the leaves of the tree. After all, if the caterpillar skips some internal node, then it will not be able to reach the subtree of this node and visit the leaves in it. Therefore, it makes no sense to teleport to the root from a non-leaf (otherwise it would be more profitable to move to the root earlier, and all the leaves would remain visited).
The optimal path of the caterpillar on the tree can be divided into movements from the root to a leaf, movements from one leaf to another, and teleportations from a leaf to the root. Let the order of visiting the leaves in the optimal path be fixed. Then it makes no sense to teleport from the last leaf, as all the leaves have already been visited. In addition, it is not profitable to move not along the shortest path in the sections of transition from the root to a leaf without visiting other leaves, or in movements from one leaf to another without visiting other leaves. If the leaf $$$v$$$ is visited after the leaf $$$u$$$, then teleporting from $$$u$$$ saves time of transition from $$$u$$$ to $$$v$$$ minus the time of moving to $$$v$$$ from the root. It is possible to choose $$$k$$$ leaves, without the last visited leaf, which give the maximum savings (if there are fewer leaves in the tree, or the savings become negative, then take fewer than $$$k$$$ leaves), and teleport from them. Thus, if the order of visiting the leaves is known, the optimal time can be found.
It turns out that if you take the tree and sort the children of each node in ascending (not descending) order of the depth of the subtree, and then write down all the leaves from left to right (in depth-first order), then this will be one of the optimal leaf orders. This order of sorting the tree and its leaves will be called the order of sorting by the subtree depth.
The tree can be sorted in this way in one depth-first traversal. For each leaf, it is possible to calculate how much time teleporting from it saves. To do this, it is enough to move from this leaf to the root until the first node, for which the previous node is not the rightmost child. Then the savings are the length of the path traveled minus the remaining distance to the root. Such paths for different leaves do not intersect along the edges, and the remaining distance to the root can be precalculated in a depth-first search for all nodes at once. Therefore, the algorithm works in $$$O(n \log n)$$$ time, where the logarithm arises from sorting the children of each node by the depth of the subtree.
Theorem.
There exists a shortest route for the caterpillar, in which the leaves are visited in the order of sorting the children of each node by the depth of the subtree.
Let $$$u_1, \ldots, u_m$$$ be all the leaves of the tree in the order that will result if the children of each node are sorted in ascending order of the depth of the subtree. Consider the shortest route of the caterpillar visiting all the nodes of the tree. Let $$$v_1, \ldots, v_m$$$ be the leaves of the tree, in the order of visiting in this route. Consider the maximum prefix of leaves that coincides with the order of sorting by the depth of the subtree: $$$v_1 = u_1,\ldots, v_i = u_i$$$. If $$$i = m$$$, then the theorem is proven. Now, let's assume that the next leaf is the incorrect leaf $$$v_{i+1} \neq u_{i+1}$$$.
The goal is to change the route in such a way that the time of traversing the tree does not increase, so that the first $$$i$$$ visited leaves do not change and remain in the same order, and so that the leaf $$$u_{i+1}$$$ is encountered earlier in the route than before the change. Then it is possible to move the leaf $$$u_{i+1}$$$ to its $(i+1)$s place, while maintaining the order of the first $$$i$$$ visited leaves. Then, in the same way, one can put all the leaves $$$u_{i+1}, \ldots, u_m$$$ in their places one by one and get the shortest route of the caterpillar with the desired order of visiting leaves.
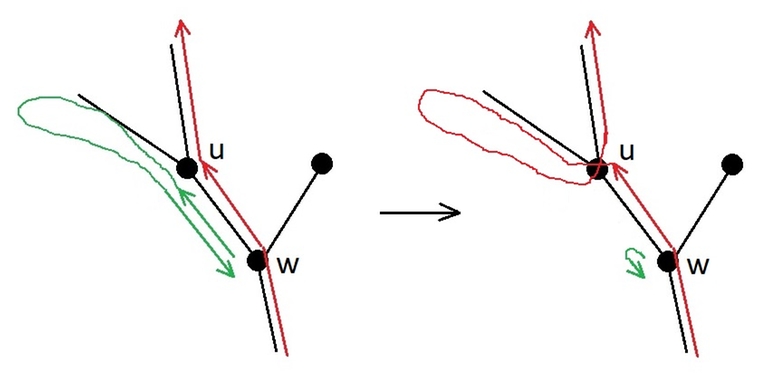
Lemma.
Let the node $$$w$$$ be the ancestor of the node $$$u$$$. Let the caterpillar in the shortest route on the tree crawl from $$$u$$$ to $$$w$$$. Then the caterpillar enters the subtree of the node $$$u$$$ only once, traverses this subtree depth-first, and returns to $$$w$$$.
Proof of the lemma.
If the caterpillar crawls from $$$w$$$ to $$$u$$$ only once, then it cannot leave the subtree of $$$u$$$ until all the nodes in this subtree are visited, and it cannot jump on a trampoline, as it still needs to move from $$$u$$$ to $$$w$$$. All this cannot be done faster than the number of steps equal to twice the number of nodes in the subtree of $$$u$$$, because the caterpillar needs to reach each node via an edge from the ancestor and to return to the ancestor. And any route without teleportations, which uses each edge twice, is one of the depth-first traversals.
If the caterpillar crawls from $$$w$$$ to $$$u$$$ two or more times, then the route can be shortened, as shown in figure.
The lemma is proven.
At the moment, the leaf $$$v_{i+1}$$$ lies in the order of visiting the leaves in the optimal route of the caterpillar in the place of the leaf $$$u_{i+1}$$$. The goal is to move the leaf $$$u_{i+1}$$$ closer to the beginning of the route, without changing the first $$$i$$$ visited leaves: $$$u_1, \ldots, u_i$$$.
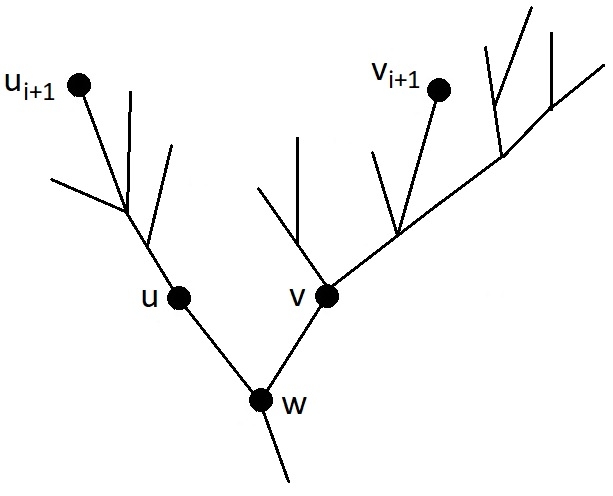
Let $$$w$$$ be the least common ancestor of the leaves $$$u_{i+1}$$$ and $$$v_{i+1}$$$, let $$$u$$$ be the child of $$$w$$$, in the subtree of which the node $$$u_{i+1}$$$ is located, and $$$v$$$ be the child of $$$w$$$, in the subtree of which the node $$$v_{i+1}$$$ is located, as shown in figure. To move the leaf $$$u_{i+1}$$$ closer to the beginning of the route, let us consider cases.
Case 1: The caterpillar in the current version of the optimal route crawls from $$$u$$$ to $$$w$$$.
In this case, according to the lemma, the caterpillar enters the subtree of vertex $$$u$$$ only once, and traverses it in the depth-first manner before returning to $$$w$$$. There are no leaves $$$u_1, \ldots, u_i$$$ in the subtree of $$$u$$$, because all the leaves of the subtree of $$$u$$$ are visited consecutively during the depth-first traversal, and the leaf $$$v_{i+1}$$$ not from the subtree of $$$u$$$ is visited after $$$u_1, \ldots, u_i$$$, but before $$$u_{i+1}$$$. Then the route can be changed as follows: the cycle $$$w \to \text{ (traversal of the subtree of } u\text{) } \to w$$$ is cut out from where it is located, and inserted at the moment of the first visit to $$$w$$$ after the visit to the leaf $$$u_i$$$. The leaf $$$u_i$$$ is not in the subtree of the node $$$v$$$, because the subtree of $$$u$$$ has a smaller depth ($$$u_{i+1}$$$ is earlier in the desired leaf order than $$$v_{i+1}$$$), and there are still unvisited leaves in it. Then, before entering $$$v_{i+1}$$$, the caterpillar will have to come from the leaf $$$u_i$$$ to the node $$$w$$$, and at that moment a depth-first traversal of the subtree of $$$u$$$ with the visit to the leaf $$$u_{i+1}$$$ will occur. This traversal was moved to an earlier time, before visiting $$$v_{i+1}$$$, which means that in the order of visiting the leaves in the caterpillar's route, the leaf $$$u_{i+1}$$$ has been moved closer to the beginning.
Case 2: The caterpillar in the current version of the optimal route does not crawl from $$$u$$$ to $$$w$$$, but crawls from $$$v$$$ to $$$w$$$.
Then the entire subtree of $$$v$$$ is traversed in a depth-first traversal. Since the leaf $$$u_{i+1}$$$ is earlier in the desired order than $$$v_{i+1}$$$, the subtree of $$$v$$$ is deeper than the subtree of $$$u$$$, and in the desired order all the leaves of $$$v$$$ come after $$$u_{i+1}$$$. Moreover, since the caterpillar does not crawl from $$$u$$$ to $$$w$$$, it is impossible to leave the subtree of $$$u$$$ except by teleporting to the root. The last jump on the trampoline from the subtree of the node $$$u$$$ is considered (or stopping at the end of the route). At this moment, all the leaves of the subtree of $$$u$$$ are visited. The route can be changed as follows: cut out the depth-first traversal of the subtree of $$$v$$$, cancel the last jump or stop in the subtree of $$$u$$$, descend from there to $$$w$$$, perform a depth-first traversal of the subtree of $$$v$$$ in such a way that the deepest node of this subtree is visited last, and teleport to the root (or stop at the end of the route). This will not be longer, because a section of transition from a leaf in the subtree of $$$u$$$ to $$$w$$$ has been added, and a section of movement from the deepest leaf in the subtree of $$$v$$$ to $$$w$$$ has disappeared, here it is important that the subtree of $$$v$$$ is deeper than the subtree of $$$u$$$. And the node $$$u_{i+1}$$$ has become closer to the beginning of the list of visited leaves, because all the leaves of the subtree of $$$v$$$, including $$$v_{i+1}$$$, have moved somewhere after all the leaves of the subtree of $$$u$$$.
Case 3: The caterpillar in the current version of the optimal route does not crawl either from $$$u$$$ to $$$w$$$, nor from $$$v$$$ to $$$w$$$.
Then all the sections of the route that move into the subtrees of the nodes $$$u$$$ and $$$v$$$ do not leave these subtrees and end with teleportation to the root or stopping at the end of the route. Among them, there is a section that starts with a step from $$$w$$$ to $$$u$$$, in which the leaf $$$u_{i+1}$$$ is visited, and a section that starts with a step from $$$w$$$ to $$$v$$$, in which the leaf $$$v_{i+1}$$$ is visited. In the current route, the section with $$$v_{i+1}$$$ comes earlier. The route can be changed very simply: swap the section visiting the leaf $$$u_{i+1}$$$ and the section visiting the leaf $$$v_{i+1}$$$. If both sections end with teleportations, then a correct caterpillar route will result. If the caterpillar stopped at the end of the section visiting $$$u_{i+1}$$$, and teleported to the root from the section with $$$v_{i+1}$$$, then now it will teleport after completing the section with $$$u_{i+1}$$$ and stop at the end of the section with $$$v_{i+1}$$$. The positions of the leaves $$$u_1, \ldots, u_i$$$ in the route will not change: they are not in the subtree of $$$v$$$, and they are not in the section with $$$u_{i+1}$$$, visited after $$$v_{i+1}$$$. And the leaf $$$u_{i+1}$$$ will get a place closer to the beginning in the order of visiting the leaves, because the section with its visit now occurs earlier in the route.
In all cases, it was possible to move the leaf $$$u_{i+1}$$$ in the optimal route of the caterpillar closer to the beginning, while maintaining the order of the first $$$i$$$ visited leaves, which means that there exists an optimal route of the caterpillar in which the leaves are visited in the order of sorting the subtrees of the tree by depth. The theorem is proven.
#include <bits/stdc++.h>
using namespace std;
const int maxn = 200005;
int d[maxn];
int h[maxn];
int p[maxn];
vector<int> leaf_jump_gains;
vector<vector<int> > children;
bool comp_by_depth(int u,int v)
{
return d[u] < d[v];
}
void sort_subtrees_by_depth(int v)
{
d[v] = 0;
if(v == 1)
h[v] = 0;
else
h[v] = h[p[v]]+1;
for(int i = 0; i < int(children[v].size()); ++i)
{
int u = children[v][i];
sort_subtrees_by_depth(u);
d[v] = max(d[v],d[u]+1);
}
sort(children[v].begin(),children[v].end(),comp_by_depth);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int n,k;
cin >> n >> k;
children.resize(n+1);
for(int i = 2; i <= n; ++i)
{
cin >> p[i];
children[p[i]].push_back(i);
}
sort_subtrees_by_depth(1);
for(int i = 1; i <= n; ++i)
{
if(children[i].size() == 0)
{
int jump_gain = 0;
int v = i;
while(v != 1)
{
int s = children[p[v]].size();
if(children[p[v]][s-1] == v)
{
v = p[v];
++jump_gain;
}
else
{
jump_gain = jump_gain+1-h[p[v]];
break;
}
}
leaf_jump_gains.push_back(jump_gain);
}
}
sort(leaf_jump_gains.begin(),leaf_jump_gains.end());
int s = leaf_jump_gains.size();
++k; //non-returning from the last leaf is like one more jump
int res = 2*(n-1);
for(int i = s-1; i >= max(0,s-k); --i)
res -= max(leaf_jump_gains[i],0);
cout << res << '\n';
return 0;
}
Author: ace5
At first, you can manually find answers for small values of $$$n$$$. For $$$n = 2, 4, 6$$$, the answer will be "YES" and the arrays will be $$$[-1, 1]$$$, $$$[-1, -2, 2, 1]$$$, $$$[-1, -2, 2, 1, -1, 1]$$$. It is not difficult to prove by case analysis that the answer is "NO" for $$$3$$$ and $$$5$$$. It can be assumed that for all odd $$$n$$$, the answer is "NO", but if you try to prove the absence of an array or find an array for $$$n = 7$$$, it turns out that the array exists: $$$[-5, 8, 1, -3, -4, -2, 5]$$$. In fact, an array exists for all $$$n$$$ except $$$3$$$ and $$$5$$$.
It would be easy if it were possible to make the number in each cell unchanged. But the presence of array edges and the prohibition of zeros make this impossible. Furthermore, it can be noticed that an infinite array in which the sequence of six numbers $$$1, -3, -4, -1, 3, 4$$$ is repeated, generates the same number in each cell as it was there. In general, any sequence of six numbers of the form $$$a, -b, -a-b, -a, b, a+b$$$ will have this property. Thus, it is possible to transform the internal cells of the array into cells with the same numbers, the question is what to do at the edges. In the author's solution, suitable edges (possibly consisting of several numbers) were manually selected for each remainder of division by $$$6$$$. And then the solution for each value of $$$n$$$ was created as follows: take the edges for $$$n \mod 6$$$ and insert into the middle as many sequences of six numbers that transition into themselves as needed.
Solution by green_gold_dog:
The idea is that any correct array can be extended by $$$2$$$ elements to remain correct. Let the array end with the numbers $$$a$$$ and $$$b$$$. Then it can be extended by two elements as follows: \begin{equation*} [\ldots,\;a,\;b] \to [\ldots, a,\; b,\; -b,\; a-b] \end{equation*} This array transitions into its permutation: the entire old array, except for $$$a$$$, is generated by the old array; the last three cells generate $$$a-b$$$, $$$a$$$, $$$-b$$$, i.e., two new elements, and the missing element $$$a$$$. It is also necessary for the new elements to be non-zero. If the last two elements of the old array were different, then the new elements are non-zero; moreover, the new elements cannot be the same, as $$$a$$$ and $$$b$$$ are non-zero, so this operation can be repeated many times.
To start, two arrays are sufficient: $$$[1, 2]$$$ for $$$n = 2$$$ and $$$[1, 2, -3, 2, 4, -5, -2]$$$ for $$$n = 7$$$. Then these arrays can be extended by $$$2$$$ to obtain the answer for even or odd $$$n$$$.
Both solutions print an array using simple rules and work in $$$O(n)$$$ time.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
if(n%6 == 0)
{
cout << "YES\n";
cout << "2 1 -1 ";
for(int j = 0;j < n/6-1;++j)
{
cout << "1 -1 -2 -1 1 2 ";
}
cout << "1 -1 -2" << "\n";
return 0;
}
else if(n%6 == 1)
{
cout << "YES\n";
cout << "-5 8 1 -3 -4 ";
for(int j = 0;j < n/6-1;++j)
{
cout << "-1 3 4 1 -3 -4 ";
}
cout << "-2 5" << "\n";
return 0;
}
else if(n%6 == 2)
{
cout << "YES\n";
for(int j = 0;j < n/6;++j)
{
cout << "1 -1 -2 -1 1 2 ";
}
cout << "1 -1" << "\n";
return 0;
}
else if(n%6 == 3)
{
if(n == 3)
cout << "NO\n";
else
{
cout << "YES\n";
cout << "2 1 1 -3 -4 -1 3 ";
for(int j = 0;j < n/6-1;++j)
{
cout << "4 1 -3 -4 -1 3 ";
}
cout << "3 -2" << "\n";
return 0;
}
}
else if(n%6 == 4)
{
cout << "YES\n";
for(int j = 0;j < n/6;++j)
{
cout << "1 -1 -2 -1 1 2 ";
}
cout << "1 -1 1 2" << "\n";
return 0;
}
else if(n%6 == 5)
{
if(n == 5)
{
cout << "NO\n";
}
else
{
cout << "YES\n";
cout << "-2 1 1 -3 -4 -1 3 ";
for(int j = 0;j < n/6-1;++j)
{
cout << "4 1 -3 -4 -1 3 ";
}
cout << "2 -1 2 4" << "\n";
return 0;
}
}
}
//#pragma GCC optimize("Ofast")
//#pragma GCC target("avx,avx2,sse,sse2,sse3,ssse3,sse4,abm,popcnt,mmx")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
typedef long double ldb;
typedef complex<double> cd;
constexpr ll INF64 = 9'000'000'000'000'000'000, INF32 = 2'000'000'000, MOD = 1'000'000'007;
constexpr db PI = acos(-1);
constexpr bool IS_FILE = false, IS_TEST_CASES = false;
random_device rd;
mt19937 rnd32(rd());
mt19937_64 rnd64(rd());
template<typename T>
bool assign_max(T& a, T b) {
if (b > a) {
a = b;
return true;
}
return false;
}
template<typename T>
bool assign_min(T& a, T b) {
if (b < a) {
a = b;
return true;
}
return false;
}
template<typename T>
T square(T a) {
return a * a;
}
template<>
struct std::hash<pair<ll, ll>> {
ll operator() (pair<ll, ll> p) const {
return ((__int128)p.first * MOD + p.second) % INF64;
}
};
void solve() {
ll n;
cin >> n;
if (n == 5 || n == 3) {
cout << "NO\n";
return;
}
cout << "YES\n";
vector<ll> arr;
if (n % 2 == 0) {
arr.push_back(1);
arr.push_back(2);
} else {
arr.push_back(1);
arr.push_back(2);
arr.push_back(-3);
arr.push_back(2);
arr.push_back(4);
arr.push_back(-5);
arr.push_back(-2);
}
while (arr.size() != n) {
ll x = arr[arr.size() - 2];
ll y = x - arr.back();
ll z = y - x;
arr.push_back(z);
arr.push_back(y);
}
for (auto i : arr) {
cout << i << ' ';
}
cout << '\n';
}
int main() {
if (IS_FILE) {
freopen("", "r", stdin);
freopen("", "w", stdout);
}
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll t = 1;
if (IS_TEST_CASES) {
cin >> t;
}
for (ll i = 0; i < t; i++) {
solve();
}
}










for problem B, could not prove why sorting one array greedily would work, but still went ahead with logic bcz it's B(not supposed to be hard). :p
I solved B using a different approach, so maybe that can help:
I want to select such an $$$i$$$ and $$$j$$$ such that $$$a_i > a_j$$$ and $$$b_i > b_j$$$ , combining these two equations I get, $$$a_i+b_i > a_j+b_j$$$, so I basically sorted in increasing order of $$$a_i+b_i$$$, then printed $$$a$$$ and $$$b$$$.
My submission: 244097120
I found this easier to understand and prove rather than the editorial solution!
Hi, I coded a solution in java based on your thought process. But I keep getting TLE. Here is my submission, help is greatly appreciated, thanks!
Hey, I am not very much familiar with Java, but what I can see is that you are using list of array, which might make it inefficient. Also, you should use the functions
BufferedReaderandStringTokenizer, which fastens the input reading speed, I have modified your code, which gives AC have a look : 245026970 (I have used 2D Array of size [n][2] which is much better than using a List of an array and used the functions I specified above for faster I/O)PS : I would recommend not using Java, because it is a very slow language, the same thing coded in C++ is way way faster.
Thanks, it really helps me a lot, I was struggling over it for days! I was also experiencing TLE with the use of an array. After formatting the results with a
StringBuilderand then printing it out, the TLE is eliminated. The performance is about 1000ms.Replacing the
ScannerwithBufferedReaderandStringTokenizerreduces the time taken to 500ms.I am currently using Java because my upcoming Uni course includes a lot of modules involving Java, so I want to familiarize myself with it. But I will definitely pick up C++ when I have more bandwidth. (I am indeed envious to see the editorial's C++ code that prints out elements one by one without an explicit buffer like
StringBuilderin Java and completes in 100ms!)Nice to hear that it finally works :)
Oh, fine, then you can continue in Java, but yeah C++ is like crazy fast.
yes your approach is very intuitive, very good thanks.
If you take a look at each $$$(i, j)$$$ pair for both $$$A$$$ and $$$B$$$ you have two cases:
1) $$$A_i>A_j\hspace{0.15cm}{and}\hspace{0.15cm}B_i<B_j$$$ (or vice versa). this means that no matter how you permute $$$A$$$ & $$$B$$$, you'll get exactly 1 inversion from pair $$$(i, j)$$$
2) $$$A_i<A_j\hspace{0.15cm}{and}\hspace{0.15cm}B_i<B_j$$$. this means that its optimal to keep $$$(i, j)$$$ in this order (or to swap them if $$$A_i>A_j\hspace{0.15cm}{and}\hspace{0.15cm}B_i>B_j$$$) no matter what.
So when you sort one array, you remove all inversions from case #2 pairs and only keep unavoidable inversions from case #1 which is optimal.
How to prove that this is a minima point and not a local minima point
All case #1 inversions cannot be removed, each of them will always add 1 to the total number of inversions no matter how you permute A and B. Case #2 inversions however can be removed and by sorting A or B you are getting rid of all case #2 inversions. It is not a local minima point because case #1 inversions are unavoidable across all possible permutations.
Is it possible to get different answers when either of a or b is sorted at once?
Let's say if a is sorted then we get total number of inversions as Na, but if b is sorted then it is Nb. will Na=Nb always?
I wasted a lot of time trying to prove it or find some other solution but couldn't do either, so in the end I just submitted with fingers crossed :p. I got lucky.
Let's make the first array $$$a$$$ to be sorted. Take a pair of indices $$$i$$$, $$$i+1$$$ which are adjacent and $$$a_i > a_{i+1}$$$. In this, there could be two cases. When $$$b_i$$$ < $$$b_{i+1}$$$ and $$$b_i$$$ > $$$b_{i+1}$$$, in the first case when we swap $$$a's$$$ element the total number of inversions will remain the same and in the second case, total number of inversions will decrease by one (elements on the right and left indices of $$$i, i+1$$$ does not effect the two cases differently). So, if we follow a process where only adjacent elements are swapped and reach the state where the first array $$$a$$$ is sorted then the number of inversions will either decrease or remain the same. Such a transition is possible because for example, Bubble sort works that way. Now, if there exists a third state of the array in which both of the arrays are unsorted and this state has even a lower number of inversions (let's say) then we can always do the above process and get to the sorted state (with same or lower number of inversions), thus proving that the sorted state is one of those states which have the lowest number of inversions.
Making a wrong submision is better than Trying Proving it for 1 hr.
Great Contest.
There is also a different non-randomized solution to E:
First, locate elements $$$1$$$ and $$$n$$$ with $$$3n$$$ queries each, similar to the editorial. After doing this, the value of $$$x$$$ will be $$$1$$$ (or $$$n$$$, depending on in which order we locate them). Now, anytime we want to change the value of $$$x$$$, we can do that by querying the position of $$$1$$$ or $$$n$$$.
We will now run a parallel binary search to find the values of all elements: For each element $$$a_i$$$, store a range $$$[l_i, r_i]$$$ in which this element must lie and iterate over all ranges in increasing order of $$$\left\lfloor\frac{l_i+r_i}{2}\right\rfloor$$$.
On one iteration we will initialize $$$x = 1$$$ and increase its value until $$$x = n$$$, handling all binary searches by querying when $$$x = \left\lfloor\frac{l_i+r_i}{2}\right\rfloor$$$. We need $$$n$$$ queries to move $$$x$$$ from $$$1$$$ to $$$n$$$. We need one binary search query for every element of the array, which is another $$$n$$$ queries. Every binary search query can move $$$x$$$ in the incorrect direction by one step, which we also need to revert with another query — yet another $$$n$$$ queries. Thus, we need at most $$$3n$$$ queries for one iteration of the binary search. It might seem like we need another $$$n$$$ queries to reset $$$x$$$ from $$$n$$$ back to $$$1$$$, but here we can be clever: If $$$x$$$ ends at $$$n$$$ after one iteration of binary search, we can do the next in decreasing order by moving $$$x$$$ from $$$n$$$ to $$$1$$$. Thus, on the iterations of the binary search we will end up alternating with $$$x$$$ going from $$$1$$$ to $$$n$$$ and from $$$n$$$ to $$$1$$$.
How many iterations of binary search do we need? Due to how we get info from the queries, an interval of length $$$w$$$ will become an interval of length at most $$$\left\lceil\frac{w-1}{2}\right\rceil$$$. We can show that going from $$$w = 2000$$$ to $$$w = 1$$$ takes at most $$$10$$$ steps — thus we need at most $$$10$$$ iterations of binary search.
We use at most $$$2\cdot 3n + 10\cdot 3n = 36n \le 40n$$$ queries in total.
Implementation: 244173268
Damn, I was thinking binary search and dp. But couldn't figure out the dp part. Great contest though
A small thing in the editorial in D:
The time complexity should be $$$O(n\ logn\ log(n*10^9))$$$ instead of $$$O(n\ logn\ log10^9)$$$.
tbhsame thing considering $$$O(\log(nX))=O(\log n+\log X)=O(\log X)$$$ when $$$X \gg x$$$
so is this legal: O(nlognlog10^9) = O(nlognlog10^2 + nlognlog10^7) and then ignore 10^2 term cuz 10^7 >> 10^2
Yes, and $$$O(n logn) = O(n/100000 * logn)$$$. When you calculate complexity of the solution and write it in O-notation, you have to assume that there is no big constant in real complexity.
You can even say that $$$O(nlognlog10^9) = O(nlogn)$$$, because $$$10^9$$$ is a constant. Do not take notations too seriously, its meaning is to approximate
In Problem D how do we know that the answer is Binary Searchable can anyone prove it ? how is a monotonic Space being Generated
Late reply, but you don't need to binary search on the "exact" answer. Instead, binary search on the condition "can we get a minimum less than equal to this value". Then it is obvious to see that it is monotonic, as if we can get a minimum less than equal to x, obviously we can get a minimum less than equal to y if x < y
hehe i got it thanks btw
I solved C in similar way , suppose $$${a > b}$$$ and $$${d = a - b}$$$ find the positions where the $$${i}$$$ bit in $$${a}$$$ is $$$1$$$ and $$$0$$$ in $$${b}$$$ , when flipping one position in $$$a$$$ and $$$b$$$ where the previous condition is met we reduce the difference $$${d}$$$ by $$$2^{i+1}$$$ when $$$d\geq2^{i+1}$$$. Store those values in array c in descending order and decrease $$$d$$$ by $$${c_i}$$$ while $$$\Sigma^k_0{c_i}{\leq}2r$$$.
I'm not really understanding how we can do E using the non-randomised in comfortably less than $$$40n$$$ queries. Here's my thought process. Use $$$6n$$$ queries to find $$$n$$$ and $$$1$$$, then to find $$$\frac{n}{2}$$$, we need to increment $$$x = 1 \to \frac{n}{2}$$$, then when we query an element, either it's bigger,smaller, or equal to $$$\frac{n}{2}$$$. If it's bigger or smaller, then $$$x$$$ will be incremented or decremented in the wrong direction, so we query either $$$1$$$ or $$$n$$$ to correct $$$x$$$.
We then go to the next element and repeat. In the worst case, this takes $$$O(n)$$$ turns (suppose $$$\frac{n}{2}$$$ is the last element or something). However, since we need to query $$$1$$$ or $$$n$$$ each time to correct, it's actually order $$$2n$$$. Then, we need to query every other element to get its relative position. This takes $$$O(n)$$$ time. So in total, we have $$$\frac{n}{2} + 2n + n = \frac{7}{2}n$$$.
This would be fine since $$$\frac{T(n)}{n} = \frac{\frac{7}{2} n + 2T(\tfrac{n}{2})}{n} \approx 39.2 \leqslant 40$$$ when $$$n = 2000$$$, but in the divide and conquer step, we need to first handle the left side and then the right. This would require decrementing $$$x$$$ (which is now $$$\frac{n}{2}$$$) to 1 then we need to bring it back up to deal with the left side, so this is going to take $$$\frac{n}{2}$$$ probably which leads to overall time complexity of $$$\frac{T(n)}{n} = \frac{4 \cdot n + 2T(\tfrac{n}{2})}{n} \geqslant 40$$$ when $$$n = 2000$$$. Also the $$$6n$$$ queries used at the beginning can hurt too.
What's wrong with my analysis?
I had a parallel binary search after finding 1 and n, my worst case is 39n. Limits definitely werent lenient for my approach.
I had a similar parallel binsearch solution.
Keep all non 1 and non n values in array, start by assigning 1 to all of them and each time try to add $$$2^j$$$ (11 bits max). Each time you sort all values, minimise x (i.e. call $$$? pos(1)$$$ until you get '=' response), then go through all values in increasing order. Increase x if necessary to get to $$$val + 2^j$$$, after that you check if actual value is lower or not. If not, you add $$$2^j$$$. After that you return to the previous value by calling 1 or n and continue.
Now this didn't quite pass, because you get about 4N calls per each cycle and we have 11 bits, but we can simply switch direction each time we pass a cycle (i.e. one time in increasing order then one time in decreasing and so on) so that we don't have to waste N queries to restart our value each cycle.
This solution uses at worst 3N (find 1) + 3N (find n) + 11*3*N = 39N queries
I think some of your steps aren't needed which is adding unnecessarily to the total number of operations.
So initially, in $$$6n$$$ queries we find $$$1$$$ and $$$n$$$, and we use $$$\frac{n}{2}$$$ queries to set $$$x = \frac{n}{2}$$$ for starting the 'quick sort' algorithm. We will add these separately to the final answer.
From what I understand in your logic, you first use $$$2n$$$ operations to get the position of $$$\frac{n}{2}$$$, and then you use another $$$O(n)$$$ steps to find out the relative positions of the other elements with respect to $$$\frac{n}{2}$$$. Instead of doing this in two steps like this, once you've gotten $$$x = \frac{n}{2}$$$, you can just check all the elements in a single run to see if they're bigger or smaller than $$$\frac{n}{2}$$$ in $$$2n$$$ steps ($$$2n$$$ because we need to do an extra query to bring $$$x$$$ back to $$$\frac{n}{2}$$$ after every query). In this process, we will also find the location of $$$\frac{n}{2}$$$. Then similar to quick sort you place all the smaller elements to the left of $$$\frac{n}{2}$$$ and bigger elements to the right.
After this, we need to set $$$x$$$ for the left and right recursive calls accordingly, to be precise, $$$\frac{n}{4}$$$ and $$$\frac{3n}{4}$$$. This will take another $$$\frac{n}{2}$$$ steps. So in total you have $$$2n+\frac{n}{2} = \frac{5n}{2}$$$ steps.
$$$\frac{T(n)}{n} = \frac{\frac{5n}{2} + 2T(\frac{n}{2})}{n}$$$ which will give $$$\frac{T(n)}{n} \approx 28$$$. In addition to this, we had $$$6n+\frac{n}{2}$$$ queries in the beginning. So overall, we can complete everything in less than $$$35n$$$ steps, which is well within the limit.
Thanks, this made sense. I completely missed the fact that you could check relative order while on the route to finding $$$\frac{n}{2}$$$.
Just one thing I'm a little confused on. When you say we need to set x for the left and right recursive calls respectively, we start $$$x = \frac{n}{2}$$$. Then it needs to go down to $$$\frac{n}{4}$$$ and once it's done, it could be at 1 (worst case I'm assuming), so bringing it up to $$$\frac{3n}{4}$$$ could take $$$\frac{3n}{4}$$$, so that "bridging" step could take $$$\frac{n}{4} + \frac{3n}{4} = n$$$.
Then, $$$\frac{T(n)}{n} = \frac{3n + 2T(\tfrac{n}{2})}{n} \approx 33.9$$$, so overall when factoring in the initial $$$6n$$$, it's just barely under 40, which I suppose does work (granted my assumption above holds).
Actually I was also thinking about this exact same thing, good that you asked.
So once we are done with the current step ($$$x = \frac{n}{2}$$$), we will decrement $$$x$$$ from $$$\frac{n}{2}$$$ to $$$\frac{n}{4}$$$ for the left recursive call. Imagine a tree like recursion structure here, so from the root, we go to the left call with $$$x = \frac{n}{4}$$$, then we process all of the recursions in the subtree of this, and once this is done, then we go to the right node of the root, (the one with $$$x = \frac{3n}{4}$$$).
So, if you think about it, since we are doing recursion in a root->left->right order (kind of like a preorder traversal), the last call that is processed in the left ($$$x = \frac{n}{4}$$$) subtree will be the node with $$$x = \frac{n}{2} - 1$$$ (it will be the rightmost leaf in the left subtree). So before we start the right recursive call ($$$x = \frac{3n}{4}$$$), the last call before this would have already set $$$x$$$ to $$$\frac{n}{2} - 1$$$. So we will only have to increment $$$x$$$ from $$$\frac{n}{2} - 1$$$ to $$$\frac{3n}{4}$$$ to go from the left recursive call to the right one.
Overall, the 'bridging' step only involves decrementing $$$x$$$ from $$$\frac{n}{2}$$$ to $$$\frac{n}{4}$$$, and then incrementing $$$x$$$ from $$$\frac{n}{2} - 1$$$ to $$$\frac{3n}{4}$$$. That comes out to be $$$\frac{n}{2} + 1$$$ operations. The rest of the steps, i.e. from $$$\frac{n}{4}$$$ to $$$\frac{n}{2} - 1$$$ will be taken care of in the subsequent recursion calls inside the left subtree. Let me know if this makes sense, I'm also not completely sure if it's correct but it seems right to me.
This makes perfect sense, thanks!
D is solvable in O(nlog(maxa)) using deque.
More specifically, a monotonic queue. It is a popular interview problem to maintain maximum/minimum in a sliding window in $$$O(n)$$$ time.
Yes. It is interesting that monotonic queue (deque) to maintain minimum can be extended to the two pointers, not just a fixed-width sliding window.
Problem B can be solved in $$$O(n)$$$. We know exactly where to place elements of sorted $$$b$$$ knowing the order of elements in $$$a$$$:
as i understad:
During contest someone hacked this 244128703 randomized E submition which use rand() without seed.
Then my randomized E submission 244133027, which happened to be identical to mentioned one, failed on auto generated after hack sys test 26.
I am not sure what to think about it :)
always use something like srand(timestamp) i guess
How about just using a better RNG?
"Do better" is great advice, thanks.
Is there any chance that you can recommend something specific? mt19937 rnd(537) from editorial is also determined by seed as far as i can tell
do some work yourself, "good random number generators c++ codeforces" google => https://mirror.codeforces.com/blog/entry/61587 first result, read it.
So the problem with rand() max_N does not apply to E because n <= 2000 and have nothing to do with my "I got hacked LOL" problem. AND mt19937 share same vulnerability with rand if you use const seed.
And you just decided to write "do better" because you read about "better" than rand() random.
and... your E submission use rng(timestamp)
which is somehow better than srand(timestamp)?
Problem D has very poor test cases. My n^2log(n) solution got passed in 93ms.
https://mirror.codeforces.com/contest/1918/submission/244154127
But if we take n = 10*5 and a = [1, 2, 3, .... , 1e5 — 20] + [1e9] * 20. Then it gives TLE
https://mirror.codeforces.com/contest/1918/submission/244190578
PS I hope the contest gets rejudged, and I hope I can have a positive delta [currently -4 :(].
can we do the DP part of problem D using top down dp ? I cant really figure it out .
In Problem D how do we know that the answer is Binary Searchable can anyone prove it ? how is a monotonic Space being Generated
For problem B, my code had passed the pretests during contest. But in one of the main tests it says wrong answer Integer parameter [name=b[i]] equals to 0, violates the range [1, 20] (test case 16788) I don't understand, since I am just taking the input and sorting it there's no way 0 should appear in the output right? https://mirror.codeforces.com/contest/1918/submission/244094541 What am I doing wrong here?
Your
compfunction should use<operator instead of<=because Compare requires strict weak ordering. Check https://en.cppreference.com/w/cpp/named_req/Compare for more details.Wow. I never knew that thanks for letting me know. You are right, my submission was accepted after just changing the
compfunction. https://mirror.codeforces.com/contest/1918/submission/244208943Amazing problemset. Overall a good contest! :)
Bhai how to be good at implementation based problems? Any advice plzz
did anyone found any similarities between today's problem c and previous codechef round's problem xorry 1? in the problem xorry 1 it was given that, for a given x find a and b such that their xor is x and their difference is minimum .so if a^b=x then a=b^x and b=a^x ,which means the question was to find a and b |a^x-b^x| is minimum.
Yes they were almost same questions
ooaa will you add a feedback vote for this contest? Here's a recent example how to use it to collect feedback about problems.
In B sorting arrays by $$$a_i+b_i$$$ also AC: 244212811
Logic is that if $$$a_i$$$ is at index $$$i$$$ then it makes least number of inversions.
Funnily enougth, any type of sorting, that forbids $$$a_i > a_j$$$ and $$$b_i > b_j$$$ for $$$i < j$$$ will work(you can prove that fact similar to editorial proof). So, if you want, you can sort by $$$a_i$$$, by $$$b_i$$$, or by $$$10a_i + 3b_i$$$
Can you prove the latter case? Why will it work for $$$10a_i + 3b_i$$$ ?
As long as you are not creating pairs with $$$2$$$ inversions (in editorial terms) what you lose in $$$a$$$ you save in $$$b$$$. So $$$10a+3b$$$ is almost $$$1a+0b$$$ (editorial solution)
D problem (Blocking Elements) Video Solution: https://youtu.be/ZfqWLxBG-Ow?si=WxQOHwg_hdelqH4C
About G, can anyone explain how the construction for n=7 came to mind? Or what was the general direction of the attempt? Thx :)
I found a smaller construction by implementing a brute-force in Python:
Output:
C using Digit DP 244113917
Can you explain the idea of using dp ?
why does this gives negative values for vary large numbers eventhough i defined int as long long globally
If 2^x does not fit in integer type but fits in long long, then you need to use 1LL << x instead of 1 << x.
I had a different solution for G and I think its much easier.
so we say that if we have a good array of size n ending in x, y (and x is not equal to y) we can achieve a good array of size n+2 like this:
a1 a2 a3 ... x, y, -y, x-y
if we denote the sum of ai neighbours by ci its array compared to a is like this:
a1, a2, a3, ... x, y, -y, x-y
c1, c2, c3, ..., cn-1, x-y, x, -y
and we know that c1 to cn-1 is a permutation of a1 to an-2 and an(aka y)
and we have -y, x-y, x in both arrays the new array of size n+2 is good.
but we still have to be careful that |ai|<=10^9.
if the two last numbers were 2, 1 the numbers that we add is like this:
2, 1 -1, 1 -1, -2, 2, 1
so it repeats it self and |ai| won exit 10^9.
for the examples of 4 and 7 we can use these:
-1, -2, 2, 1
-1, 4, -1, -3, -2, 2, 1
so that was my solution!
very good contest
In the tutorial of the problem F it is stated that it is possible to choose k leaves, without the last visited one and teleport from them, but for the first example of the problem you can not achieve the cost 9 without teleporting from the node 6, which would be the last traversed leaf if we sort the children of each node by depth. Additionally, in the code k is increased by 1 to show that you are allowed to do one extra jump to the root as you are not returning from the last leaf, but even though it is wrong, my intuition would be to consider just the gains between each consecutive pair of leaves (choosing k of them) and not take into consideration the distance from the last leave to the root, as you won't take this jump. Can someone clarify please?
Wrong. You can reach cost $$$9$$$ while ending at $$$6$$$: $$$1 \rightarrow 3 \rightarrow 7 \rightarrow 3 \rightarrow 8 \overset{\text{teleport}}{\rightarrow} 1 \rightarrow 2 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 6$$$
Am I misunderstanding, or are you saying that your intuition is wrong? Anyway, your intuition is correct, and so is the editorial. Considering or not considering the path ending in a leaf as an extra teleport doesn't make any difference, as that teleport would always be the most time saving one, so you'd always choose that in both cases.
Regarding problem F, I was wondering how people came up with the idea during the round. Did you guyz prove your approach or just tried a few intuitive things because the idea doesn’t seem very obvious. Just curious to know.
problem B: can be solved by using vector of pair too.Well its the same idea like the tutorial.Just used vector of pair, instead of array of pair. - If anyone need here is the Submission
Deleted
The second case (when we set 1 in x at the position of the first differing bit) is analyzed similarly, but in fact it is not needed because the answer will not be smaller, and x will become larger.Can someone explain and prove this?
The problem C was very good. I thinked on it one and half hour
why in problem c I have to make the bit in a equal to 1 only if its already 1 in b
and if the position is differing, then we will set a 1 in a⊕x at this position if possibleif its 0 in b and in a then making it 1 on both numbers should make no difference but I tried that and it give me wrong answer on test 2 so why would making a digit equal to 1 on both numbers make any difference ?
edit: I just figured out why its because doing this process will make x gets larger with no benefit at all and I want to make x large only when it is beneficial for me
Can anyone help me understand what am i doing wrong in C? Here is my Solution.
My approach : make a > b. As long as the ith bit of a and b are same, do nothing, if they are different, for the first time it happens, set ith bit of x such that ith bit of a becomes 1 and ith bit of b becomes 0, from then on keep the ith bit of x such that exact opposite happens. now in the same iteration, check the ith bit of r, if x and r are equal at that bit, do nothing, for the first time they are unequal, if the ith bit of r is not set and ith bit of x is set, set the ith bit of x to 0, this will ensure that x is definitely going to be smaller than r, for the rest of the iterations dont check the size of r and x. I do want to first set the ith bit of x acc. to a and b, then check later if i can or not by comparing it to r. Is the approach itself wrong or am i missing out something in the implementation? Ive broken my head for enough time over this, help a brother out folks. Thanks in advance.
Take a look at Ticket 17321 from CF Stress for a counter example.
I understand the testcases are not working. I just cant figure out why.
Did you try to dry run the testcase that I shared? It's literally the smallest possible counter example, with just 2 integers (1 and 2, and there are only 2 possible values of $$$x$$$ (0 and 1). Just read through your explanation and replace $$$a$$$, $$$b$$$ and $$$x$$$, you'll see at what point did an incorrect bit get added to the answer.
I did, and I figured the reason for why it wasnt running last night only, there was no way i couldnt debug it for large TCs. Later i figured i was using one more flag unnecessarily. Fixed it now. Thanks for your help.
I think there's a mistake in problem D's editorial. It states "less than l and not greater than r", but I think he meant "at least l and not greater than r".
I wonder if in B the arrays A and B were not permutations but general integer arrays such that each element is distinct in the two arrays individually, then would sorting still be optimal or not? Can someone help
As we never care about the true values of the integers (i.e. we never do arithmetic on them) and instead, we just care about their relative order (smaller vs larger), the exact values don't matter and can be anything, as long as they're distinct (because original values were distinct). This is the same reason for why coordinate compression works, just in reverse.
I don't understand, why x += (1ll<<i) and x += (1<<i) in C give other results, can somebody explain it pls? I think it's connected to difference between int and long long types, but I don't understand how it's working.
see this comment
int is 32 bit and long long is 64 bit. So if left shift by more than 31 you will get integer overflow as it will pass the limit of integer. So that's why use long long here.
B. Minimise The Inversions
The total number of inversions in a' and b' should be the minimum possible among all pairs of permutations that can be obtained using operations from the statement.
Doesn't this mean we should reduce the inversions in a and b as much as possible.
Doesn't it convey a different meaning convey a different meaning from
total no of inversions in a and b combinedshould be minimum as possible.Consider the input
a=[2, 3, 1]b=[3, 1, 2]the answera' = [1, 2, 3]b' = [2, 3, 1]is being considered a valid solution but,a inversion count = 0andb inversion count = 2.Consider the answer
a = [1, 3, 2]andb = [2, 1, 3]this is a valid solution and yet the total no of inversions in a and b are (1, 1) as supposed to (0, 2) in the previous answer. isn't this the correct answer since we are supposed to keep the inversions in a and b to minimum rather than keep both of them combined to minimum ?no, the statement should be read in full it is The total number of inversions in a' and b' should be the minimum
I see greedy in Problem D's tag. Just wondering if anybody is aware of any greedy solution to this problem
In Problem C, If anyone has done it using dp then please share your idea $$$/$$$ code.
someone posted above
If you want to test your understanding of Problem D: Blocking Elements, you can try out ABC334F: Christmas Present 2. I also have a video editorial and practice contest for the latter.
can we do the dp part of problem d using top down dp ? I cant really figure out . Or you could just make a video editorial for this problem D ?
Yes, why not? You can close your eyes and convert your iterative DP to recursive if you wish.
For example, here's my iterative DP, and here's the same code converted to recursive DP
If you're talking about the set optimization, then yes, you would need iterative DP, the same way you need iterative DP in prefix sum / sliding window optimizations.
Yes actually optimization was my main issue . Thanks for the reply .
Did anyone solve c greedily starting from least significant bit/(lsb) /right to left?
About problem B.
Tutorial proves that we cannot get a better solution by changing ONLY ONE pair of ij. But what if we change MORE than one pair of ij? I think it's not obvious, because the proof need array a to be sorted.
I use the same mothod(just prove the condition of moving one step) to prove greedy problems but I keep doubting this. XD
Why is the order of visting the leaves in the editorial for F optimal?
In the tutorial for F,
To do this, it is enough to move from this leaf to the root until the first node, for which the previous node is not the rightmost child.
I couldn't understand this sentence. Can anyone explain this please?
Deleted
D can be solved in Nlog(10 ^ 9) instead of NlogNLog(10 ^ 9).
We can use monotonic queue to get the minimum, instead of a set
My Submission :
https://mirror.codeforces.com/contest/1918/submission/245363349
Good questions
Can someone please explain what i am doing wrong in C here is my submission -> https://mirror.codeforces.com/contest/1918/submission/245687089
Take a look at Ticket 17333 from CF Stress for a counter example.
Thanks Ser!
Alternative solution to F using Aliens trick and CHT:
Let $$$b_1, \dots, b_m$$$ be the leaves of the tree in DFS order. We want to select a subsequence of size at most $$$k + 1$$$ to minimize
$ where $$$a_1, \dots, a_{k + 1}$$$ is the chosen subsequence.
First of all, let's consider ending the path as another jump to the root. Let's count the contribution of each edge to the answer. Let $$$x$$$ be the number of selected leaves in the subtree of $$$u$$$. Notice that if $$$x = 0$$$ the edge between $$$u$$$ and $$$p_u$$$ will be traversed 2 times. Otherwise it will be traversed $$$x$$$ times. This simplifies into the above formula.
This can be calculated with dp. After guessing that the answer is convex for increasing $$$k$$$, we can apply Aliens trick. This reduces the complexity from $$$\mathcal{O}(n^2k)$$$ to $$$\mathcal{O}(n^2 \log n)$$$.
Let's now notice that $$$d(\mathrm{lca}(b_i, b_k)) \leq d(\mathrm{lca}(b_j, b_k))$$$ for $$$i \leq j \leq k$$$. This property allows us to apply CHT, and to find intersections we can use binary search. This makes the final complexity $$$\mathcal{O}(n \log^2 n)$$$, which is fast enough.
Submission
I find this solution quite educative jaja I mean, using 2 dp optimization looks unbelievable.
I think the following mental picture makes the proof for F a lot better:
Firstly, consider the sequence of all vertices visited in the optimal route. Observe that $$$w$$$ must occur between $$$u_i$$$ and $$$u_{i + 1}$$$, since $$$u_i$$$ must not exist in $$$u$$$'s subtree (or else our proposed solution wouldn't pick $$$v_{i + 1}$$$). Similarly, $$$w$$$ must occur again between $$$u_i$$$ and $$$v_{i + 1}$$$. The path then looks something like $$$u_i, ..., w, ..., u_{i + 1}, ..., w, ..., v_{i + 1}, ...$$$.
Case 1: If $$$w$$$ occurs again sometime after $$$v_{i + 1}$$$, swap the blue and the red: $$$w, \color{blue}{..., u_{i + 1}, ...,} w, \color{red}{..., v_{i + 1}, ...,} w, ...$$$
Otherwise, let $$$r$$$ be the root of the tree. Then the path looks something like $$$w, ..., u_{i + 1}, ..., w, ..., v_{i + 1}, ..., r, ...$$$. Here, the particular $$$r$$$ we care about is either the $$$r$$$ teleported to after the last leaf in $$$v$$$'s subtree is visited, or an imaginary "extra" jump if that last leaf was the last leaf visited in the entire tree (just like in the editorial).
Case 2.1: If $$$r$$$ occurs between $$$u_{i + 1}$$$ and the following $$$w$$$: $$$w, \color{blue}{..., u_{i + 1}, ...,} r, ..., w, \color{red}{..., v_{i + 1}, ...,} r, ...$$$
Case 2.2: It doesn't. Then we can swap the following parts: $$$w, \color{blue}{..., u_{i + 1}, ...,} w, \color{red}{..., v_{i + 1}, ...,} r, ...$$$, and do the thing described in case 2 of the editorial (crawl back to $$$w$$$ from the last leaf in the red, and jump to $$$r$$$ from the deepest leaf in the blue).
This also relies on it being true that the optimal route won't ever enter $$$u$$$'s subtree more than once, but it's much more obvious now. The proof for that is also restricted to this case, and didn't motivate the casework to begin with, unlike the lemma in the editorial — I don't think it's obvious at all why someone would start by proving that lemma.
Here's a completely different solution for problem F. This is just a general idea, not an attempt to prove its correctness or explain in detail.
Let's slightly modify the problem. We'll require returning to the root using teleportation after visiting all nodes, but we'll also increase $$$k$$$ by 1. Note that this problem is equivalent to the original one.
Let's now solve this problem instead. If we choose a set of leaves $$$S$$$ from which we'll teleport to the root, and visit all of them in optimal order, it can be shown that the total cost of the path is equal to $$$2n-2-(2 |E_S| - \sum_{v \in S} depth(v))$$$, where $$$E_S$$$ is the set of all edges leading from the root to the nodes in $$$S$$$. Let $$$f(x)$$$ be the optimal cost we can get if $$$|S| \leq x$$$. Notice that the function $$$f(x)$$$ is increasing and concave, so we can apply the slope trick to find $$$f(k)$$$ without explicitly setting the limit for the size of the set $$$S$$$. We can do this by adding a penalty function to $$$f$$$, so instead, we're trying to optimize $$$f(x)-p|S|$$$ for various values of $$$p$$$. We binary search for the smallest value of $$$p$$$ which results in us taking no more than $$$k$$$ elements. This arrangement is then the optimal solution. Code: 253393999
I could not get the editorial for problem B , how come sorting first array will make the inversions minimum, i have tried some examples manually but i couldn't understand. Any mathematical proof would be great to understand. can anyone help with that ?
Please help for problem C, I keep getting WA on test 6. https://mirror.codeforces.com/contest/1918/submission/255018640
In the editorial of problem C:
"Let's consider the bitwise representation of numbers a , b , x . Let's look at any 2 bits at the same position in a and b , if they are the same, then regardless of what is in x on this position, the number |(a⊕x)−(b⊕x)| will have a 0 at this position."
I think that this isn't always true. let us suppose a = 13 and b = 7; their binary representations are 1101 and 0111, respectively. The bits at position 3 from the end is equal for both but let us take x = 0. So $$$|a \oplus x - b \oplus x | = 0110$$$. The bit at the position 3 from the end is still one, not zero.
Please check, ace5 ooaa
In Problem D how do we know that the answer is Binary Searchable can anyone prove it ? how is a monotonic Space being Generated
https://mirror.codeforces.com/contest/1918/submission/266586169
what is wrong with this solution . It is failing on 108th case of test case 2 . Plz help.
worst worst worst explanation of C. ITS MAY WRONG TOO.
Is the proof for B complete? because I think we also need to take into account the fact that the number of inversions created in the segment of a ranging from i to j will always be more than or equal to the number of inversions undone in b, which is true because a single swap can at most undo j-i+1 inversions and any swap in a(after sorting) would always result in j-i+1 inversions.
problem B was rated 900 clown moment
1918E - ace5 and Task Order Why I got “TLE on test 1”? 297082983