lperovskaya's blog

Yandex.Algorithm 2014 elimination stage: round 2
By lperovskaya, 10 years ago, translation, In English

Will begin today, at 21:00 MSK. All paricipants, advanced to the elimination stage, are welcome to participate through the link. This round will be 100 minutes long and will be scored using Grand-Prix 30 system. First place in Round 1 gave pperm86 100 score points and invitation to the final round in Berlin! Who will reserve his place among the finalists today?

Good luck!

P.S. In case of infinite redirect loop, please, clean browser cookies or use an incognito mode

  • Vote: I like it
  • +60
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Do you know how to determine who will win T-shirts?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +22 Vote: I do not like it

    I know for sure! Check out the Awards section of rules.

    Top 150 participants of the elimination stage (more score points, then more problems solved, then with less penalty time) will receive a souvenire.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +25 Vote: I do not like it

      souvenir = T-shirt? :)

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

are the contest problem available in english also ??

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

After going through the link I'm getting "You can not participate in the contest because the registration is closed" ???

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I have advanced to elimination stage(Yandex has sent me a email for this), but when i entered to round 2 i saw this sentence: "You can not participate in the contest because the registration is closed"

What's wrong???

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Try to login maybe

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Thanks, but i've login already. I missed round 1 for the same reason above. I don't want to miss round 2 too. Any help will be appreciated.

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it -6 Vote: I do not like it

Contest for Red coders :( this round really contains very hard problemset

→ Reply
»
10 years ago, # |
  Vote: I like it +19 Vote: I do not like it

How to solve A???

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    If you fix the first black vertex (closest to the central vertex from 1 end) in a cycle of c vertices, you can pack the next few black vertices in that cycle greedily; this way, you get the distance of the 2 black vertices closest to the central vertex equal to c%K + aK ≥ K (a: any non-negative integer such that the inequality holds).

    Consider a valid solution (not necessarily optimal) where the first black vertex is fixed at some distance d from the central one, and the last one (in that cycle) is at a distance d' such that |d - d'| > 1. You can rotate the black vertices by 1 now, in such a way that the respective distances are d + 1 and d' - 1 (or d - 1 and d' + 1), so |d - d'| decreases by 2 and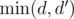 increases by 1. This solution is also valid, so we can use this rotation and fix 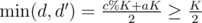(integer division).

    This tightest greedy packing of black vertices makes all pairs of black vertices in 1 cycle satisfy the condition, and the smallest distance between 2 vertices from distinct cycles is the sum of 2 smallest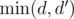 -s. In case K is odd and there are x ≥ 2 cycles for which that number is 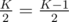(first division: integer, second: exact), we fail; otherwise, we win.

    If we fail, we need to increment a for at least x - 1 cycles; then, we get the situation with x ≤ 1, and win. So we just need to find the obvious greedy bound B on the number of black vertices, sum of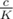 (integer division, when taking each cycle independently), the number x of cycles for which 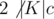and correct the bound B to B - (x - 1) (if x > 0). I hope it was at least a bit clear :D

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For Problem D, I had the following idea, but had some problem while implementing:

Suppose we have sequence 1 2 3 4 5, then rotating the sequence would give 5 inversions -> 2 3 4 5 1 .

So I thought that I just had to calculate the amount by which a particular subsequence should be rotated to come closer and closer to K inversions.

e.g.:

For K=8,

Initially: 1 2 3 4 5

Step1:  K -  = 4 2 3 4 5 1

Step2:  K -  = 3 3 4 5 2 1

Step3:  K -  = 1 4 3 5 2 1

So the answer would be 4 3 5 2 1

Is my approach correct? How do I implement it? Or is there a simpler approach to go about it?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The number of inversions in your answer is 7, not 8.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Edited. Could you describe your method please?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it +1 Vote: I do not like it

        Let inv[n] = n*(n-1)/2. Find the smallest n, such that inv[n] >= k. The first number in permutation is k-inv[n-1]+1, the others should be put in the decreasing order.

        → Reply
»
10 years ago, # |
  Vote: I like it +6 Vote: I do not like it

How to solve B?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    1. Note that a bigger module does not influence after a smaller one, or if an initial number is smaller.

    2. So we have a non-increasing subsequence, ending with the smallest number, and we can ignore other numbers.

    3. Sort the numbers and run by them in non-increasing order. Keep in used[] array the set of numbers we have. Initially this set is empty.

    4. At each step, take all the available numbers modulo a[i], add the results to the set and also add the number a[i] to the set (as an initial number).

    5. There are some tricks with the smallest number. It can be unique or not.

    6. The total time is O(largest number * N).

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks. I used exactly the same approach, but failed on test 18 :( The "trap" was that if smallest number is present in the array more than once, we should not add it to the set on the last step.

      → Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

I solved problem D, using Binary Search. First I find what is length of permutation such that total numbers of inversion is closer to k using the binary search. ** (No of inversion = n * (n — 1) / 2) ** as maximum value of k can be 10 ^ 9 so I took upper limit as 10 ^ 5 + 1 and lower as 0.

Suppose we Got permutation of length as length , this length of inversion as inversion Now I Got length of permutation, so now I have to make this so no permutation of inversion Should be equal to K.

So inside while loop taking condition as while (inversion> k) do binary search on permutation from 1 to length such That (inversion — (length — (After Binary search result))> = K) Then I Add it int array.

Print it first and print the remaining one in decreasing order.

for example; k = 4 after binary search it will give length of permutation as 4 (No of inversion is 6).

step 1 -; 6> 4: after binary search on permutation from 1 to n we find that 2 is best because (6 — (4 -; 2)) gives us 4 which is greater than equal to k.we add 2 in array.

step 2 ; 6 == 4: loops break; print length; print elements added in array. print remaining element in decreasing order so output 4 2 4 3 1 I got accepted in second time because I added wrong element.

Edit- It got posted in Russian, so need to paste it again in english. My solution

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

In Gym: 2014 Yandex.Algorithm - Elimination Stage, Online Round 2

В Тренировках: 2014 Yandex.Algorithm - Elimination Stage, Online Round 2

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    Почему задачи A и E совпадают?

    → Reply
»
10 years ago, # |
  Vote: I like it +20 Vote: I do not like it

Solution for problem E (user requested):

Suppose that there are two triples (ua, ub, uc) and (va, vb, vc) such that uaa + ubb + ucc = vaa + vbb + vcc. Then (ua - va, ub - vb, uc - vc) is an integer multiple of some fixed triple which could be found by solving a linear system. Let that triple be (da, db, dc). Suppose that da, db, and dc are nonnegative (actually, changing their sign doesn't affect the answer). From every triple (ua, ub, uc), where each of ua, ub, and uc is between 0 and N - 1, subtract (da, db, dc) while the result is still within those bounds. The final set will contain the points which have either ua < da, or ub < db, or uc < dc. The number of such points is N3 - (N - da)(N - db)(N - dc), and this is the answer. However, if either of da, db, or dc is at least N, the answer is just N3. Total complexity: O(1) (ignoring the GCD computation).

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I solved it in O(N2) by trying all ua - va, ub - vb, computing the necessary uc - vc for them and checking how many solutions they take out. A really simple solution. Pity that I didn't do this problem instead of F during the contest, I would've probably gotten a better place (at least thanks to time) :D

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve F? My idea was for each of the 3 permutaions, we can get cycle lengths of the permuations, and then we can take 3 cycles from 3 permutaions, and for all 3 cycle combination count how many coin it will take to visit all grids having co-ordinates in those 3 cycle combination, add these to get the result. But time complexity becomes O(N^3). How to do this?

→ Reply