Hello codeforcers, since the editorial for 1930G - Подсчет множества префиксных максимумов is not out yet, and I found the problem to be pretty cute, I decided to write this blog.
Note:
- I will refer to "prefix maximum array" as PMA for the sake of brevity.
- By "possible" PMA, I mean a PMA which can be generated by some valid partial pre-order traversal.
Let us firstly make a couple of general observations:
- If element $$$u$$$ occurs as a prefix maximum in any possible PMA, then the values of all its ancestors must be less than $$$u$$$.
- If elements $$$i, j$$$ $$$(i < j)$$$ occur as adjacent prefix maximums in any possible PMA, then we have two cases:
- $$$i$$$ is an ancestor of $$$j$$$ : Here, $$$i$$$ must be the largest (indexed) ancestor of $$$j$$$.
- $$$i$$$ is not an ancestor of $$$j$$$: Here, let $$$c$$$ be the first node on the path from $$$lca(i, j)$$$ to $$$i$$$. $$$i$$$ must be the largest (indexed) node in the subtree of $$$c$$$ and $$$i$$$ must be larger (indexed) than the largest (indexed) ancestor of $$$j$$$.
Now, let's think about a slow solution, what if we were allowed to solve the problem in $$$O(n^2)$$$?
Well, a relatively simple idea that comes to mind is the following:
Define $$$dp_u$$$ to be the number of distinct PMA's we can get from a partial preorder traversal which ends at $$$u$$$, such that $$$u$$$ is the last element of the PMA.
Now, we try to compute all $$$dp_u$$$ in increasing order of $$$u$$$. Notice that the second last element $$$v$$$ in any PMA ending with $$$u$$$ must be $$$< u$$$, so to compute $$$dp_u$$$, we can iterate over every possible second last element $$$v$$$, and add the number of possible PMA's ending with $$$[v, u]$$$ to $$$dp_u$$$. It's important to fix the second last element to prevent overcounting (you will realise the motivating ideas later).
You now say, how do we find the number of such possible PMA's ending in $$$[v, u]$$$ for some given $$$u$$$ and $$$v$$$?
- For there to exist any PMA ending with $$$[v, u]$$$, the conditions mentioned in observation $$$2$$$ must be satisfied by $$$v$$$ and $$$u$$$.
- If the mentioned conditions are satisfied, then it can be shown that for every possible PMA ending with $$$v$$$ (call it $$$P$$$), it is possible to generate the PMA $$$P + [u]$$$. This is true because:
- If $$$v$$$ is an ancestor of $$$u$$$: Simply go directly from $$$v$$$ to $$$u$$$ while performing the preorder traversal, and this will result in the PMA $$$P + [u]$$$.
- If $$$v$$$ is not an ancestor of $$$u$$$: Perform the preorder traversal for the entire subtree of $$$c$$$ (same definition as in observation 2.b) and then go directly from $$$lca(u, v)$$$ to $$$u$$$. This results in the PMA $$$P + [u]$$$.
So, we now have a concrete $$$O(n^2)$$$ dp.
Optimizing this solution from $$$O(n^2)$$$ to $$$O(n\log{n})$$$ is honestly the easiest part of the problem and is a decent exercise as an implementation task on trees. I would advise you to try and do it yourself (there are several ways to do so).
I will just give a basic sketch of my (kinda ugly) implementation here. I won't go into as much detail as I did for describing the dp formulation because this blog is already way too long.
For any node $$$u$$$ (which doesn't trivially have $$$dp_u$$$ = 0), we make the following observations:
- The only ancestor which contributes anything to $$$dp_u$$$ is the largest indexed ancestor (call it $$$mx$$$). (refer to observation 1 to see why this is true)
- Other nodes which make a non-zero contribution to $$$dp_u$$$ are non-ancestral nodes.
For any non-ancestral node $$$v$$$ which makes a non-zero contribution to $$$dp_u$$$, it's easy to see that $$$v$$$ must be the maximum node in the subtree of $$$c$$$ (first node on path from $$$lca(u, v)$$$ to $$$v$$$), Since $$$v < u$$$, this means that all nodes in the subtree of $$$c$$$ are smaller than $$$u$$$.
Now, let's define a "blob node" (with respect to $$$u$$$): A blob node $$$x$$$ is a node such that all nodes in its subtree are less than $$$u$$$, and $$$u$$$ lies in the subtree of parent of $$$x$$$. We also define the representative of $$$x$$$, $$$rep_x$$$ to be the maximum indexed node in the subtree of $$$x$$$ (Clearly, $$$rep_x < u$$$).
Claim : Any non-ancestral node $$$v$$$ ($$$< u$$$) which contributes something to $$$dp_u$$$ will be the representative of some blob node.
Proof : Exercise for the reader, I am too tired.Let there be two sets of blobs : The set of Red blobs $$$R$$$ ($$$rep < mx$$$) and the set of Green blobs $$$G$$$ ($$$rep > mx$$$).
This entire structure can be visualized in the following manner:
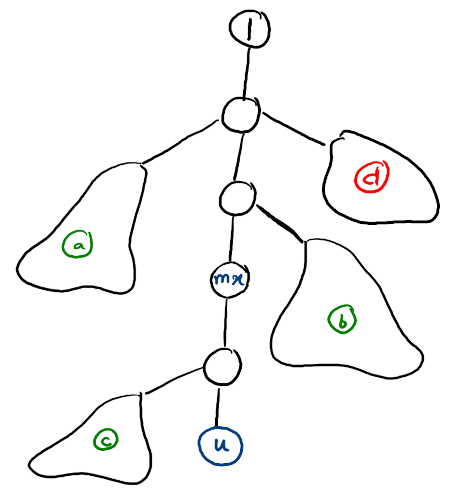
($$$mx$$$ is largest ancestor of $$$u$$$. $$$a$$$, $$$b$$$, $$$c$$$ are green blobs. $$$d$$$ is a red blob, it can be shown that parents of all red blobs are ancestors of $$$mx$$$).
Clearly, $$$dp_u = dp_{mx} + [\sum{dp_{rep_x}} (x \in G)]$$$
Which can be rewritten as $$$dp_u = dp_{mx} + [\sum{dp_{rep_x}} (x \in (R \cup G)] - [\sum{dp_{rep_x}} (x \in R)]$$$
Now, how do we implement this?
Maintaining blobs is pretty easy, you just have to keep pushing them upwards (see the remove() function in my code). For querying the second term for some $$$u$$$, we do the following: For any blob $$$x$$$ we will store $$$dp_{rep_x}$$$ at $$$par_x$$$ in some path sum query structure. Then, the second term is simply the sum on the path from the root node to $$$u$$$. Note that as the blob nodes move upwards/merge, you will have to make this change reflect in the path sum structure.
As for the third term, this is a bit more tricky. It can be shown that the third term is actually equal to the (second term when $$$u = mx$$$), so for each node, we have to store the second term separately because it might be used later.
Surprisingly, the implementation isn't too cancerous: 247534020










Perform the entire preorder traversal for c (same definition as in observation 2.a) and then go directly from lca(u,v) to u. This results in the PMA P+[u].
It is meant preorder traversal for subtree of c?
proof for last claim "third term is actually equal to the (second term when u=mx)"?