The number is the "law" if it consists only of digits 3 and 5 or if it is divisible by the number that is law.
For example, the numbers 3, 53, 66, 106 are "law" numbers, and 16, 34 and 56 did not.
How many there are "Law" numbers greater than or equal to A and smaller than or equal to B?
input
The first line contains two integers A and B (1 ≤ A ≤ B ≤ 10^9).
output
The first and only line of output as the "law" of numbers in the interval [a, b].
Examples:
entrance
1 10
output
5
entrance
171 822
output
315
Any idea how to solve it?
Since A,B <= 10^9, there are only 2^9 different numbers consisting of only 3's and 5's. Precalculate these and put into a list, making sure that you do not put a number that is divisible by any of the numbers already in the list.
Let F(A) = # of law numbers in the interval [1,A]. Then we seek F(B)-F(A-1).
F(X) can be calculated as follows: for i = 0 ... size(list) d = list[i], ans+= X/d-F(X/d) ; return ans;
not sure though
This actually helps a lot. I ran a bruteforce on small B and it seems that there are just 22 such numbers for B = 105. Just thanks to divisibility by 5, we can decrease the obvious bound of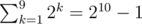
to 29 - 1 (the last digit must be 3) and this bound is further decreased by other divisibilities.
This means we have what, 200 numbers up to 109? That's quite a decent number for backtracking, especially considering these numbers won't have many common factors and most of them are huge. Consider the inclusion-exclusion principle: add all numbers divisible by one law-number, from them subtract all numbers divisible by some 2 law-numbers, add numbers divisible by a set of law-numbers of size 3, etc. In this case, if you took a set of size at least 3, you'd most likely just need to add/subtract numbers divisible by something much larger than 109. And that's 0 under these constraints. So all you need to do is backtrack all sets of divisors (trying to add all divisors larger than the largest one so far in the set, and removing the one added last when it's not possible anymore), add/subtract the numbers in the desired range divisible by all divisors in the set (or equivalently, by their LCM), and if you encounter a state where this LCM is large, just go right back from it. Complexity: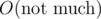
:D
smallest law numbers which can't be divided by previous law numbers — 3, 5, 53. How is 3 * 5 * 53 = 795 much larger than 10^9?
12th smallest out of law numbers which aren't divisible by any other: 3·104. Multiply 3 such numbers and you get over 1013. And there are very few small numbers, so there are very few sets where this doesn't hold.
I said "if you took a set of size at least 3", meaning arbitrary set, not the smallest one, then you'd most likely (with high probability for random choices, e.g. it holds for most such sets) end up with large LCM.
Why should I always choose a set of small divisors? It doesn't work that way.
You do not choose them arbitrarily, you need to iterate over ALL of them to use inclusion-exclusion principle, right?
Looks like I didn't got your point initially and you were saying that even though for some of them you might need to iterate the sets with more than 3 items but the number of such sets with product less than 1^9 will be very small. Is that correct?
Yup, that's it.
Now that I think about it, since the numbers composed of 3/5 increase very fast, maybe we don't need to ignore the ones divisible by some other to get a working backtrack...
Thank you all for your comments. After I read all this I wrote a solution that you can see on the link http://pastebin.com/3NNQvT9j