Heyo! If you tried to solve problem D you have probably ended up trying to optimize this algorithm:
But of course this won't work! The number of values in dp[i] will grow exponentially. But we only need to output first K values of the final dp[0]. Can we do better?
We only need to store first K values for each dp[i]. So we can rewrite: dp[i] = cur; while (dp[i].size() > k) dp[i].pop_back();
This leaves us with O(n^2 k) solution, this time the bottleneck is the merging part. The OFFICIAL solution is to use priority queue to select first K values after merging, without going through all values. But we are not interested in that!
LAZY solution
If you have heard about Haskell, you might know that it's a lazy language, it only computes things when it absolutely needs them -- e.g. when you print them. Could it be the case that just switching our programming language to Haskell make the solution pass? (Spoiler: yes, kindof)
Skeleton of Haskell code
Note: Codeforces is sometimes showing single dollar sign as 3 dollar signs, I don't know how to prevent that.
The code above reads the input into 2D array arr such that we can access element as arr ! (i, j).
Now we need the merge function, it takes 2 sorted lists and returns merged one:
merge :: [Int] -> [Int] -> [Int]
merge (x : xs) (y : ys) =
if x > y
then x : merge xs (y : ys)
else y : merge (x : xs) ys
merge [] xs = xs
merge xs [] = xs
Pretty simple if you know the syntax, but it's not very important.
Now to rewrite the core of the algorithm above (it's possible to do this without recursion but it's less readable):
let
calc dp (-1) = head dp
calc dp i = calc (curdp : dp) (i-1)
where
prepareMerge j dpval =
if j < i then dpval
else map (+ (arr ! (i, j))) dpval -- add arr[i][j] to every element
tofold = zipWith prepareMerge [(i-1)..] dp
curdp = ...
putInts $$$ take k $$$ calc [[0], [0]] (n-1)
The base case is when i=-1, we just return dp[0]. dp stores the values of dp[i+1..n+1] for each iteration, instead of storing the full dp array. This better fits recursive implementation.
Where clause declares variables: tofold stores all the lists that we want to merge. Now consider:
curdp = foldr merge [] tofold
foldr function applies merge to every element from right to left:
merge(tofold[0], merge(tofold[1], ... merge(tofold[m-1], [])))
Now our submission 254204408 confidently passes in 1300ms
How easy was that?
We are not even truncating dp[i] every iteration, we take first K values only at the end!
The catch
I have no idea how the above works. It should've worked in O(n*n*k) but it looks like working in O(n*n + k), it's either GHC magic or the tests are weak.
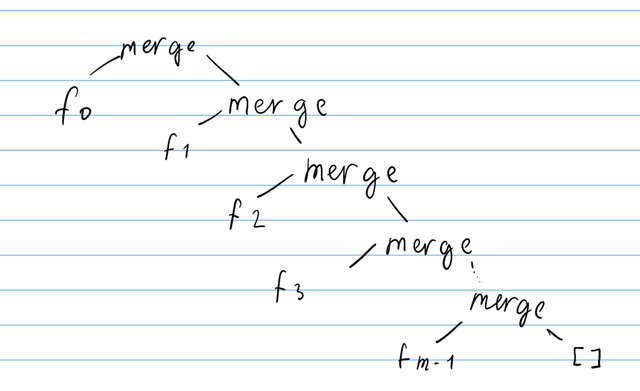
Anyways, foldr version leads to this computation tree:
To get the first element of the array, Haskell might have to go through each merge node to find the smallest element. So the worst case for merging NxK arrays is O(nk), but if we use divide and conquer to merge the arrays:
mergeAll [] = []
mergeAll [arr] = arr
mergeAll arrs = merge (mergeAll (take mid arrs)) (mergeAll (drop mid arrs))
where mid = length arrs `div` 2
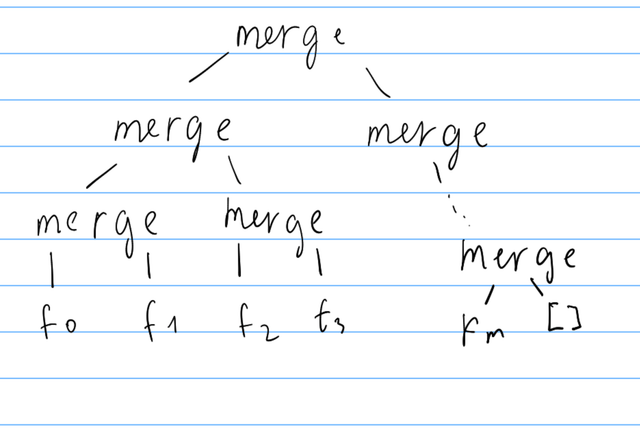
This leads to this computation tree:
This way haskell will only have to go compare and go down O(log n) merge nodes to find the next smallest element. Now our submission 254204435 passes in 2500ms.
Python solution
If you look at Accepted python submissions to problem D you will see there are only 5 (!!) submissions. This is because python doesn't have builtin priority queue and writing PQ in python is very slow.
Adapting the lazy solution to python is possible by using half baked python feature called generators.
This is the submission 254208539 (...yeahhh.. merge function is very long in python). The foldr version is TLEing for some reason, I really have no idea how that passes in Haskell. The divide and conquer version passes in 4100ms. Note that we are using lazy only to merge the lists. We are using normal lists when storing them in dp[i]. This is because generators can be only consumed once in python, while Haskell lists act as both lazy lists and generators, depends on your view.
Conclusion
This was one of the coolest things I've done with Haskell (including outside of CP) and I wanted to share it :)










drdilyor our favorite doge tester
orz
I'm not familiar with Haskell, but this doesn't seem like magic to me — your Haskell foldr solution looks like it should run in $$$O(n(n+k))$$$. The reason is that each path takes $$$O(\text{maximum depth of the computation tree})$$$ to compute, and the maximum depth of the foldr computation tree if you consider all $$$i$$$ simultaneously is $$$O(n)$$$. This is because every time you go down the computation tree, you move right one position in the painting.
Your Python foldr solution is not equivalent — as you mentioned, it runs in $$$O(n^2k)$$$ time.
Thanks you so much for the explanation! But I still don't get why this foldr doesn't work with python:
Is there some strictness introduced that Haskell version doesn't have? Haskell version also has to evaluate every list in
tofoldto at least the first element (because of how merge works). This didn't work too: 254338913. Maybe the merge function is wrong in Python. Reifyingmergefunction into a class didn't work though.Your Python solution evaluates the first $$$k$$$ elements of each $$$dp[i]$$$. The Haskell solution doesn't necessarily do that, so it can be faster.
Here's a C++ solution that does what I think the Haskell solution is doing: 254348521
Also in Python (though it gets MLE or TLE): 254347951
Thanks, that was indeed the culprit! Taking first $$$k$$$ elements and using deepseq to force them to evaluate makes foldr solution TLE. 254362368. Now I better understand how foldr version works.
Auto comment: topic has been updated by drdilyor (previous revision, new revision, compare).